3月AT杂题
ABC292
Ex 太一眼了，不写了。
F - Regular Triangle Inside a Rectangle
题意：给你一个大小为 \(a\times b\) 的矩形，求矩形内部能放下的最大正三角形的边长。
\(\text{O}(\log n)\) 做法：假设 a<b ，发现最优的情况一定是这样的：
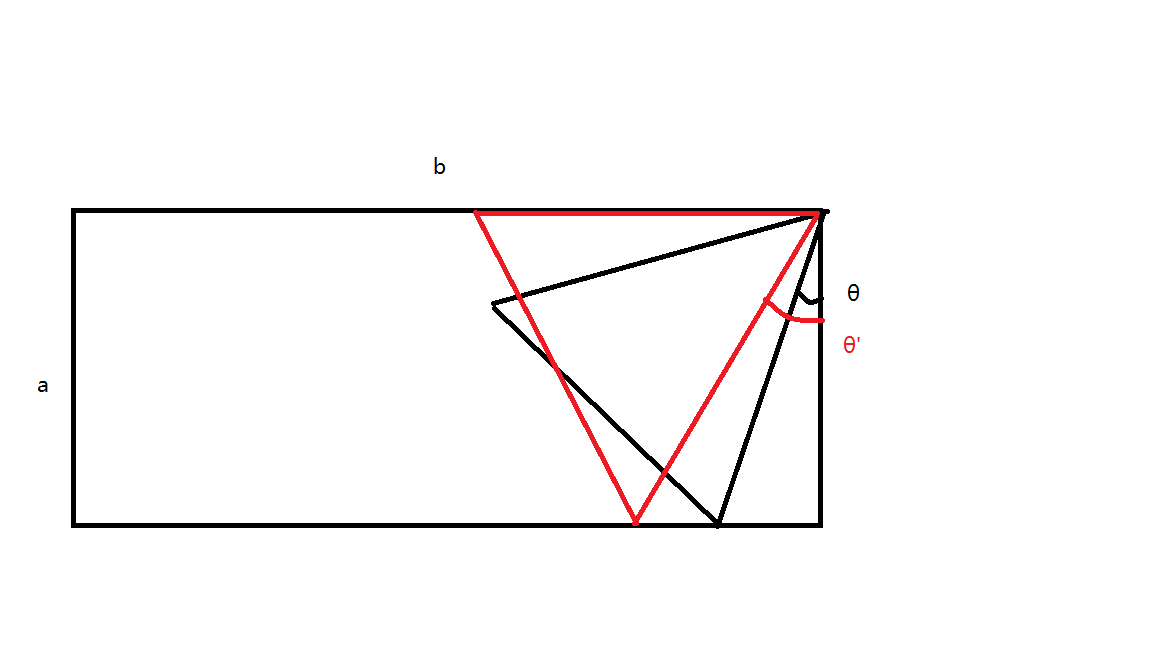
即夹角 θ 越大，正三角形边长越大，于是考虑二分（我也不知道 check 怎么写的，瞎 jb 乱写就过了）。
\(\text{O}(1)\) 做法：因为最优情况一定是一个顶点在矩形顶点，还有一个在边上，思考另一个点怎么运动。发现这是瓜豆原理，画出另一个点运动的轨迹，根据长边是否够长分类讨论即可。
G - Count Strictly Increasing Sequences
题意：给你 n 个长为 m 的数字串（包含 '?' ）， '?' 可以替换成任意数字，求替换后使得 n 个串组成的数字单调递增的方案数。 \(n,m\le40\) 。
思考什么时候有两个数 \(s_i,s_j\) 单调递增，这只会有两种情况： \(s_{i,1}<s_{j,1}\) 或 \(s_{i,1}=s_{j,1}\) 且 \(s_{i,2\dots m},s_{j,2\dots m}\) 单调递增。这是一个类似递归的定义，我们可以把后面的情况看做子问题。定义 \(f_{l,r,x,k}\) 表示对于 \(s_l,s_{l+1}\dots s_r\) ，仅考虑 \([x,m]\) 这几位，且第 x 位满足 \(s_{i,x}\ge k\) 的方案数。显然前面有一些数的第 x 位相等，剩下的数第 x 位递增。所以转移就是枚举断点，前后方案数相乘。还有一种可能是没有哪一位出现 k 这个数，此时方案就是 \(f_{l,r,x,k+1}\) （注意边界的处理）。
ABC293
F - Zero or One
题意：给你一个 n ，求有多少个 b 满足 \(b>2\) 且 n 在 b 进制下每一位为 0 或 1 。 \(n\le10^{18}\) 。
对于 \(b^4\le n\) 的所有 b ，个数不会超过 \(\sqrt[4]{n}\) 个，暴力枚举判断即可；对于剩下的 b ，可以枚举 n 在 b 进制下每一位的值，二分求是否存在这样的 b 即可。
PS： 有人 发现这是 oeis 上的 数列 ，但是上面只有 \(\text{O}(\sqrt{n}\times\log_b{n})\) 的做法，所以没什么用。
G - Triple Index
题意：查询区间内满足 \(i<j<k,c_i=c_j=c_k\) 的三元组 (i,j,k) 的个数。可离线， \(n,m,c_i\le2\times10^5\) 。
莫队板子。不会的去看 P1494 [国家集训队] 小 Z 的袜子 。
Ex - Optimal Path Decomposition
插眼。
ABC294
怎么 AT 现在又那么板了啊，乐。
F - Sugar Water 2
题意： Takahashi 有 n 杯糖水，其中第 i 杯中有 \(a_i\) 克糖和 \(b_i\) 克水。 Aoki 有 m 杯糖水，其中第 i 杯中有 \(c_i\) 克糖和 \(d_i\) 克水。求两人各选择自己的一杯糖水混合能产生的浓度第 k 大的浓度为多少。 \(n,m\le5\times10^4\) 。
考虑二分答案，浓度不小于 x 的条件等价于 \(a_i-x\times a_i-x\times b_i\ge -c_i+x\times c_i+x\times d_i\) ，前面后面都能预处理。枚举前面，二分求个数即可。时间复杂度 \(\text{O}(\text{c}n\log n)\) ， c 是二分次数。
G - Distance Queries on a Tree
板子 +1 。
题意：给一棵树，支持修改一条边的边权和查询任意两点距离。 \(n,q\le2\times10^5\) 。
是 P1505 [国家集训队]旅游 的弱化版，树剖随便过（这个 trick 实在是太板了，不知道有多少道原题）。
PS：可以 BIT 维护 dfn 序上前缀和，查询就是找一下 lca ，都是 \(\text{O}(n\log n)\) 的。
Ex - K-Coloring
插眼。
ABC295
E - Kth Number
题意：长度为 n 的数列 a，\(a_i\in[0,m]\)。对于 \(a_i=0\) 的 i，将 \(a_i\) 等概率替换为 \([1,m]\) 中任意一个数，求 a 第 k 小值的期望。\(n,m\le2000\)。
令 \(s_i\) 表示使得第 k 小不大于 i 的替换方案数，\(c_i\) 表示 a 中不小于 i 的个数（不包括 0），\(z\) 表示 0 的个数，则 \(s_i=\sum\limits_{j=k-c_i}^{z}\dbinom{z}{j}\times i^j(m-i)^{z-j},ans=\dfrac{\sum\limits_{i=1}^n(s_i-s_{i-1})*i}{2^{z}}\)。
F - substr = S
题意：定义 \(\text{f}(x,s)\) 表示在数字 x 中字符串 s 出现了多少次（例如 \(\text{f}(2223,'22')=2,\text{f}(123,'4')=0\)）。给一个字符串 s（可能含有前导零），求 \(\sum\limits_{i=l}^r\text{f}(i,s)\)。\(\left|s\right|\le16,l,r\le10^{16}\)。
转化成 \(\sum\limits_{i=1}^r\text{f}(i,s)-\sum\limits_{i=1}^{l-1}\text{f}(i,s)\)。枚举 s 在 i 中出现的位置，根据与上限的关系可以算出方案数。特判前导零。
G - Minimum Reachable City
题意：给一棵有向的树 T（保证初始时 u 的任意祖先的编号都小于 u），支持两个操作：选择 \((u,v)\)（保证有路径可以从 v 到 u），连一条 \(u\rightarrow v\) 的边；求 x 能到达的所有点中（包括自己）编号最小的。\(n,q\le2\times10^5\)。
加边的操作就相当于让 \(v\rightarrow u\) 路径上所有点答案都变成 v，考虑 dsu 维护。加边的时候把 u 的祖先全部连到 v 上，查询时直接查祖先的答案即可。
