2月杂题

叠甲：

本博文中出现所谓难度评价大部分为作者自己根据自己的水平以及其评分所认定的难度，含有较大主观性，仅供参考，切勿当真。

作者水平有限，可能会收录很傻逼/一眼的题目，只是一个类似总结的东西，还请多多谅解。

怎么会有人 3 月了还在填 2 月的坑啊（）。

C0181 【0128 C组】模拟测试

D 【0128 C组】多

占坑。（神题，可能永远不会填，放个 $\text{g}\text{rass8cow}$ 的 题解）

C0184 【0204 C组】模拟测试

D 【1127 C组】树

占坑。（难写，可能暂时不会填，等我调出来/dk）

AtCoder Beginner Contest 289

F - Teleporter Takahashi

题意：给你一个坐标 $(sx,sy)$，每次可以选择在一个给定矩形内的一个点，将坐标变为以这个点为对称中心的另一个端点，能否使得最后坐标变换到 $(tx,ty)$。输出方案。所有坐标 $\le 2\times {10}^5$，方案操作次数 $\le {10}^6$。

首先横纵坐标互不影响，可以分开考虑。思考变换对 $sx$ 带来的影响：第一次，变换中心是 $p$：$sx\to 2p-sx$ ；第二次，变换中心是 $q$：$2p-sx\to 2q-(2p-sx)=sx+2(q-p)$；

即两次变换可以看做是将坐标加上一个偶数。同时，由于 $sx\equiv sx+2n\equiv 2m-sx(\mathrm{mod}2)$，发现起始与终止坐标奇偶性不同时一定无解，记 $c$ 表示 $tx-sx$。所以可以构造出一种方案：每次选 $a,a+1$ 让 $c\to c-2$。减法和纵坐标类似。如果横纵坐标操作次数不同，就在少的后面随便加上一些相同的操作即可。有一些坐标相同或矩形较小的情况需要特判。

C0187 【0210 C组】模拟测试

C 【1204 C组】雾雨魔理沙

首先判掉原本就是回文串和重排后也构不成回文串的情况。有一个显而易见的性质：假如区间 $[l,r]$ 满足条件，那么包含它的 $[L,R]$ 也一定满足条件。思考怎么找最小的满足条件的区间：找到极长的前缀 $[1,l-1]$ 和后缀 $[r+1,n]$ 使得 $s_1+s_2+\cdots +s_{l-1}$ 等于 $s_n+s_{n-1}+\cdots +s_{r+1}$。发现要找的最小区间一定在区间 $[l,r]$ 里面，思考它的形态。

如果有一个最小区间为 $[x,y]$，其中 $l<x\le y<r$，那么意味着左右两边一定有公共的前后缀，而这与我们“极长”的定义不符，故最小区间只会是 $[l,r]$ 的一个前或后缀。以前缀为例：比如一个元素在区间内出现了 $c$ 次，那么我们前缀区间的右端点 $L$ 至少要取到：

$L=\{\begin{array}{ll}{p}_{\frac{c}{2}}& c\equiv 0(\mathrm{mod}2)\\ max\{p_{\lfloor \frac{c}{2}\rfloor +1},\lfloor \frac{l+r}{2}\rfloor \}& c\equiv 1(\mathrm{mod}2)\end{array}$

其中 $p_i$ 表示这个元素第 $i$ 次出现的位置。$max\{p_{\lfloor \frac{c}{2}\rfloor +1},\lfloor \frac{l+r}{2}\rfloor \}$ 是因为那个数必须安排到中点。最后求出了前缀区间的右端点 $L$，后缀区间的右端点 $R$，容斥即可。

Educational Codeforces Round 143 (Rated for Div. 2)

D. Triangle Coloring

题意：给定 ${\displaystyle \frac{n}{3}}$ 个三角形，每条边都有一个权值。现在给 $n$ 个点分别涂上 ${\displaystyle \frac{n}{2}}$ 个红色和 ${\displaystyle \frac{n}{2}}$ 个蓝色，使得所有端点颜色不同的边的权值和最大，求上色方案数。所有权值 $\le 1000$。

发现一个三角形要么两个同色一个异色，要么全部同色。但是我们可以证明前者更优：假如有两个三角形分别涂了 3 个红色和 3 个蓝色，那我们可以把他们改成 2 红 1 蓝和 1 红 2 蓝，这样一定更优。那么每个三角形的贡献就是权值最大的两条边。计数，乘系数。

E. Explosions?

题意：有一个长度为 $n$ 的序列，定义一次操作是将序列中一个大于 0 的数 $x\to x-1$。你可以进行任意次操作，使得整个序列 >0 的位置构成一个严格的单峰，求峰顶大小+操作次数之和的最小值。

$\mathcal{O}(n\log n)$ 做法：首先左右情况对称，可以只考虑左边怎么做。严格递增，故 $a_j\le a_i-(i-j)$，移项得 $a_j-j\le a_i-i$。记 $c_i=a_i-i$，每次相当于要找到最近的使得 $c_j\le c_i$ 的 $j$，树状数组维护。

$\mathcal{O}(n)$ 做法：考虑将一连串的相差为 1 的高度合并为一个“阶梯”状的图形。考虑单调栈维护，每次加入的时候操作所有阶梯头不小于当前阶梯尾的栈尾元素。

F. Blocking Chips

题意：有一颗大小为 $n$ 的树，树上有 $k$ 个点初始为黑色且放有棋子，其余节点为白色。棋子每次移动到相邻的一个白色节点并将其染黑，第 $i$ 次移动第 $(i-1)modk+1$ 颗棋子，求最大移动次数。$n\le 2\times {10}^5$。

发现直接做不出来，考虑二分答案转化为判定性问题。自下而上操作每个点。每个点移动的最优策略是优先向子树走，否则向父亲移动直到当前点可以向其子树移动。记录三个数组 $len$ 表示子树内最长可移动路径，$vis$ 表示当前节点是否有棋子， $need$ 表示这个节点还需要走几步。

G. Removal Sequences

题意：给定一个图，每个点有一个权值 $a_i$，你需要依次删除所有点。一个点能被删除当且仅当该点的度数等于 $a_i$。求有多少点对 $(x,y)$ 满足 $x<y$ 且存在一种先删 $x$ 再删 $y$ 和一种先删 $y$ 再删 $x$ 的删除方法。保证至少有一种方案。$n,m\le {10}^5$。

神题。

首先构造一组可以全部删除的方案。记录他们被删除的次序。这个可以用拓扑排序。然后正难则反，找到所有不合法的点对。

有一个性质：一个点对 $(x,y)$ 不合法，当且仅当 $u\to v$ 的路径在拓扑序上是递增的前提下，$u$ 能到达 $v$。

充分性：

必要性：

AtCoder Beginner Contest 290

E - Make it Palindrome

题意：给一个长度为 $n$ 的序列 $a$，求其所有连续子序列 $a_l,a_{l+1}\dots a_r$ 的代价之和。这里定义代价为将序列变为回文所需最小修改次数。$n\le 2\times {10}^5$。

正难则反。先求出总次数，在减去相同的数贡献的次数。对于长为 $len$ 的连续子序列，总共有 $n-len+1$ 个，每个的全部修改的次数为 $\lfloor \frac{len}{2}\rfloor$。记数 $m$ 的所有出现位置为 $v_1,v_2\dots v_k$，以 $v_i$ 贡献的次数为例。对于 $v_i,v_j$ 且 $v_i\le v_j$，包含他们的序列有 $min(v_i,n-v_j+1)$ 个。既满足 $v_i\le v_j$ 又要求 $min$ 很麻烦，发现 $min$ 可以在每个数的位置处预处理。更具体地说，包含 $x$ 的序列最多有 $min(x,n-x+1)$ 个。

upd in 2023.2.20：原来的做法时间复杂度瓶颈在于排序的 $\mathcal{O}(n\log n)$，但是其实不用排序。发现对于递增的 $v$ 数组，$min(v_i,n-v_i+1)$ 是一个单峰的序列，可以用双指针维护比当前数大的区间。这样就优化到了 $\mathcal{O}(n)$（不过快排换成桶排好像就是 $\mathcal{O}(n)$ 了）。

F - Maximum Diameter

题意：定义序列 $a$，$a_i$ 表示点 $i$ 的度数。定义合法的序列 $a$ 的价值为所有大小为 $n$ 且符合条件的树的直径的最大值。求所有合法的序列 $a$ 的价值之和。多测，数据组数 $T\le 2\times {10}^5$，$n\le {10}^6$。

首先 $\sum _{i=1}^n{a}_i=2\times n-2$，且 $\underset{i=1}{\overset{n}{min}}{a}_i\ge 1$。这很显然。然后思考 $a$ 与直径的关系——直径 $len$ 等于 $n+1-\sum [a_i=1]$，这可以证明：首先直径中除了端点外每个顶点的度数都至少为 2，因此这是解的上界；然后我们可以通过以下方式构造一棵这样的树：先把所有度数 $>1$ 的点首尾相连成一条链，然后再把度数 $=1$ 的点附加到这条链上面。所以答案就是

$$(n+1){\displaystyle (\genfrac{}{}{0ex}{}{2n-3}{n-1})}-n{\displaystyle (\genfrac{}{}{0ex}{}{2n-4}{n-2})}$$

解释一下：我们先假定所有方案的直径长度都为 $n+1$，则总长度就是前面一坨；再减去所有方案中 1 的个数：我们钦定 $x_i=1$，则其他位置上的方案就是 ${\displaystyle (\genfrac{}{}{0ex}{}{2n-4}{n-2})}$。由于每个位置都是一样的，所以乘上 $n$ 即可。

G - Edge Elimination

题意：有一棵深度为 $d$ 的满 $k$ 叉树（根节点深度为 0），问你最少割几条边能形成一个大小为 $x$ 的连通块。

C0191 【0221 C组】模拟测试

B 【1218 C组】跳房子

神构造。

发现 $x_i\le {10}^{18}$ 这个限制很有意思，思考怎么在值域上做文章。发现 ${10}^{18}\approx 2^{60}$，且 $60\approx 2^6$。对于倍数关系，因为 $x_i$ 严格递增，那么这里跳跃的条件就是一个倍数关系，而最小的倍数关系是 2 倍。这两个关系驱使着我们想到如下构造：对于 $x_i$，记最大的满足 $2^p\le x_i<2^{p+1}$ 的数 $p$ 为 $a_i$，如果 $a_i,a_j$ 二进制下前四位相同，则把 $(i,j)$ 分配给 1；若不同，如果前两位相同，则分配给 2，反之给 3。

正确性显然（笑。

C0190 【0217 C组】模拟测试

C 【1211 C组】子图

占坑。

C0194 【0225 C组】模拟测试

B 【0225 C组】集合问题

首先很显然我们只会选至多两个区间，因为选更多的话 $and$ 不会变优，$or$ 可能更劣。把情况分成 $and=0$ 和 $ans\ne 0$ 讨论。这个很好判断，可以直接用 multiset 维护当前最大的最大的左端点和最小的右端点。

当 $and\ne 0$ 时，我们找到最小的 $and$ 的区间，在左右端点处各选一个最优的区间；否则，我们用一颗线段树来维护答案。假设当前节点维护的是 $[l,r]$，那我们就会维护 3 个信息：所有右端点在 $[l,r]$ 里面的区间的左端点的最大值，所有左端点在 $[l,r]$ 里面的区间的右端点的最小值，以及 $and=0$ 时最小的 $or$。注意我们并没有要求维护的前两个值一定在 $[l,r]$ 里。操作就是单点改，维护类似最大子段和。

C 【0225 C组】求代价

为了方便叙述，我们把问题转化为数轴上黑白的点，连边代价就是距离。每个点至少连一条边的限制并不好满足，考虑转化成至多连一条边。先找到每个点最近的异色的点，距离记作 $d{a}_i,d{b}_i$。这就是一种贪心的方案。

显然贪心是错的，考虑加入类似反悔的操作。转化后，新问题就是两个点连边的代价就是 $d{a}_i+d{b}_j-|a_i-b_j|$，每个点至多连一次，让代价最大（注意这里“连边”的定义已经改变了）。

把数轴上的点按颜色分成极长的段，可以证明两段之间连边一定是前一段的后缀与当前段的前缀对应相连最优，就是这样：

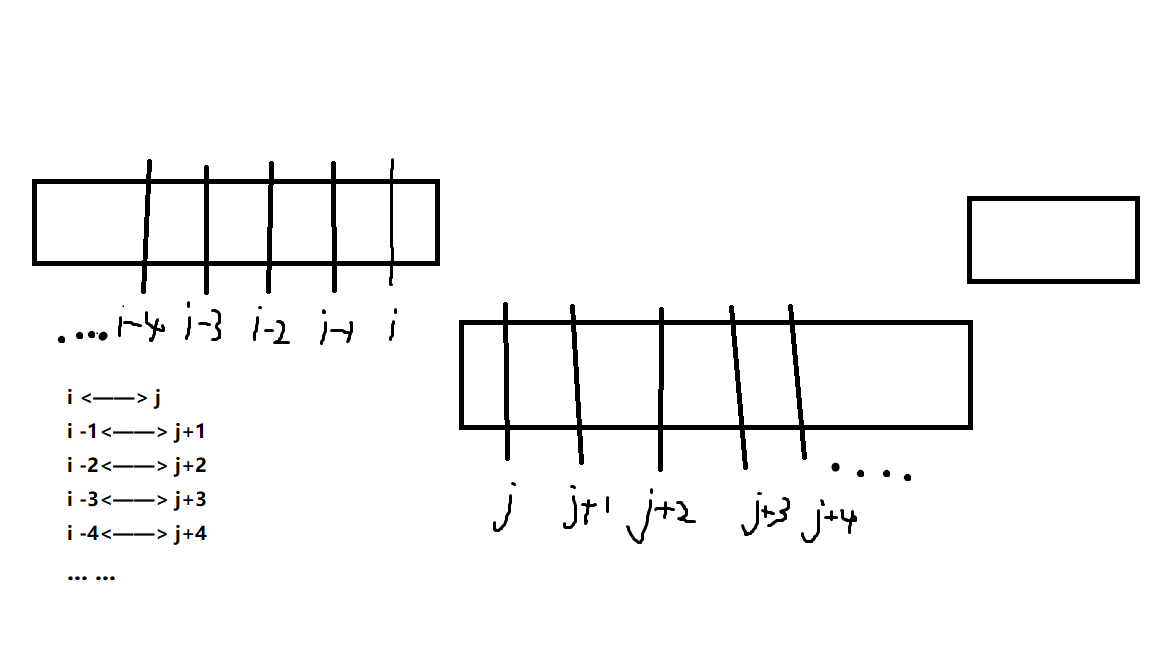
那么这就是一个简单的线性 DP。

D 【0225 C组】排列问题

占坑。现在还不会。

C0195 【0228 C组】模拟测试

D 【1225 C组】字典树

定义 $c_{i,j}$ 表示在 $s_i$ 中 $j$ 的出现次数，$f(T,i)$ 表示字符串 $T$ 是 $s_i$ 的前缀的概率，$F(T)$ 表示字符串 $T$ 是至少一个 $s_i$ 的前缀的概率，$t_i$ 表示字符串 $T$ 中 $i$ 的出现次数（注意这里我们定义中提到的是“前缀”而非“极长前缀”）。

首先可以得到答案 $ans=\sum F(T)$。解释一下：如果 $T$ 是至少一个 $s_i$ 的前缀，那么字典树里面一定会出现它；然后，对于一个前缀，他的所有前缀都会被计算一遍答案，比如 $s_i$ 有一个前缀 12345，那么 1、12、123、1234、12345 都是 $s_i$ 的前缀，都会被计算一次。

然后，我们有以下式子：

$$f(T,i)={\displaystyle \frac{\prod _{j=0}^9{c_{i,j}}^{{\bar{t}}_j}}{m^{\overline{|}T|}}}$$

$$F(T)=1-\prod _{i=1}^n(1-f(T,i))$$

解释一下：第一个式子中分母表示 $s_i$ 重排后前 $|T|$ 位是字符串 $T$ 的方案数，分子表示对每个位置具体限定其等于 $T$ 中对应位置的方案数；第二个式子很显然，不做解释。

同时，发现上式与 $T$ 具体是什么没有关系，只与 $t_0,t_1\dots t_9$ 有关。考虑枚举 $t_0,t_1\dots t_9$，对于一个十元组，发现它们构成 $T$ 的方案数为 ${\displaystyle \frac{(\sum _{i=0}^9{t}_i)!}{\prod _{i=0}^9(t_i!)}}$。

解释一下：分子表示总方案数，分母是除掉同种数字的顺序。

这样我们就得到了一个时间复杂度为 $\mathcal{O}(m^{10}n)$ 的方法，考虑优化。发现 $n$ 很小，可以把 $F(T)$ 拆成容斥的形式：

$$F(T)=\sum _{\varnothing \ne S\subseteq \{1,2\dots n\}}((-1{)}^{\left|S\right|+1}\prod _{i\in S}f(T,i))$$

考虑交换答案中求和的顺序，先枚举 $S$，再枚举 $t_i$。发现转化后答案的式子可以拆成两部分，一部分只与 $t_i$ 有关，一部分只与 $\sum _{i=0}^9{t}_i$ 有关，且前者都是乘积，可以背包计算，后者最后考虑即可。

更具体地，我们可以考虑在枚举当前 $i$ 的同时，枚举 $t_i$ 的值并计算出 $t_i=x$ 时会产生的贡献。定义 $d{p}_{i,j}$ 表示满足 $\sum _{k=0}^i{t}_i=j$ 的所有方案的贡献，即可背包转移。

Codeforces Round 848 (Div. 2)

D. Flexible String Revisit

题意：给两个 01 串 $s$ 和 $t$，每次操作是随机翻转 $s$ 的一位，求 $s$ 变成 $t$ 的期望次数。

法 1：定义 $f_i$ 表示 $s$ 从初始到当前还有 $i$ 个位置与 $t$ 不同的期望次数。有转移方程 $$f_i=1+{\displaystyle \frac{i}{n}}{f}_{i-1}+{\displaystyle \frac{n-i}{n}}{f}_{i+1}$$

发现这个东西要高斯消元，但是系数都在一条对角线上，故单次消元为 $\mathcal{O}(1)$，时间复杂度 $\mathcal{O}(n)$。

法 1.5：令 $s$ 表示初始不同的个数，发现根据数学推导可以得出法 1 中 $f_{s+1}=2^n-1$。

法 2：定义 $f_i$ 表示当前有 $i$ 个位置与 $t$ 相同，变成 $i+1$ 个相同的期望次数。有转移方程

$$\begin{array}{rl}{f}_i& ={\displaystyle \frac{i}{n}}(f_{i-1}+f_i+1)+{\displaystyle \frac{n-i}{n}}\\ \\ & ={\displaystyle \frac{n+i{f}_{i-1}}{n-i}}\\ \end{array}$$

可以直接转移。令 $s$ 表示初始相同的个数，答案就是 $\sum _{i=s}^n{f}_i$。

E. The Tree Has Fallen!

前置知识：线性基。

类似做法指路 D 【1012 D组】烤乐滋的树 。

题意：给定一棵有点权的无根树，每次询问求以 $r$ 为根时在 $v$ 的子树内选任意个点的点权异或最大值。

根据以 1 为根时点 $r$ 的位置分情况讨论：

• 如果 $r$ 在 $v$ 的子树外，那么以 $r$ 为根时 $v$ 的子树不变；

• 如果 $r=v$，那么以 $r$ 为根时 $v$ 的子树就是整棵树；

• 如果 $r$ 在 $v$ 的子树内，记 $p$ 是 $r$ 的祖先中是 $v$ 的儿子的那个，那么以 $r$ 为根时 $v$ 的子树就是 $v$ 的子树内除了 $p$ 的子树内的点。所以维护 dfs 序前缀后缀线性基，子树内线性基，每次找 $p$ 直接像求 $\text{lca}$ 一样跳就行了。

F. Maximizing Root

前置知识（其实不需要，只是顺便学习）：Binary GCD。

题意：给你一棵以 1 为根有点权的树，可以操作至多 $k$ 次，每次选择一个没有选择过的点并把它子树内所有点乘上子树内的 $gcd$，求 1 号点的最大值。

占坑。看这个。

AtCoder Beginner Contest 291

G - OR Sum

前置知识：卷积。

首先每位互不影响，可以分开考虑。然后假设已经转完，$\sum _{i=0}^{n-1}(a_i|b_i)$ 可以转化成 $\sum _{i=0}^{n-1}(a_i+b_i)-\sum _{i=0}^{n-1}(a_i\ast b_i)$。求后面那坨东西的最小值可以卷积求（实现见 atcoderlibrary）。

更具体的，atcoder 自带的卷积就是 $c_i=\sum _{j=0}^i{a}_j\ast b_{i-j}$（$c_i$ 是卷积得到的数组）。于是我们考虑翻转 $a$，再把它接一份到自己后面（因为可能要移动），直接求卷积即可。正确性可以自己列一下式子推一下，这里不做赘述。

Ex - Balanced Tree

前置知识：点分治。

题意：给定一棵树 $T$，让你构造一棵树 $R$ 满足：

• 对于点对 $(x,y)$，它们在 $R$ 上的 $\text{lca}$ 在 $T$ 上的位置是它们的路径上；

• 对于点 $x$，它在 $R$ 上的子树大小的两倍不超过他的父亲在 $R$ 上的子树大小。

占坑。

Educational Codeforces Round 144 (Rated for Div. 2)

E. Colored Subgraphs

题意：给你一棵无根树，给每个点染色，使得对于所有同色点 $(x,y)$，满足 $x\to y$ 的路径上所有点颜色与 $x,y$ 相同，且 $x,y$ 到根节点的距离不等。定义一种染色方案的价值为出现次数最少的颜色的出现次数，求最大价值。

只会 $\mathcal{O}(n\log n)$ 的垃圾做法。

题意可以转化为每次染一条从叶子往上的一条链。强制钦定根节点为 1，考虑二分答案，问题转化为了判断整棵树能不能分成向上的长度不超过 $k$ 的链。记录 $d_u$ 表示 $u$ 子树内叶子结点到 $u$ 的路径的最短长度。显然对于叶子有 $d_u=1$，其他节点有 $d_u=\underset{v\in so{n}_u}{min}{d}_v+1$。不合法的情况有两种：对一个节点 $u$ 有两个儿子 $v1,v2$ 满足 $d_{v1},d_{v2}<k$ 或者根节点 $r$ 的 $d_r<k$ 。

对于不合法的情况，记 $s1,s2$ 为 $v1,v2$ 子树内的那两条链的叶子结点。我们不能选择 $u$ 子树外的点作为根节点（因为这样子树内形态不变），也不能选择 $s1,s2$ 到 $u$ 路径上的点（因为只会让链断开，长度更短），更不能选 $u$ 的其他儿子的子树内的点（因为根本没有解决问题），所以只能选 $s1,s2$ 作为根节点。求 $s1,s2$ 可以对每个点记 $p_u$ 表示取到 $d_u$ 的链的叶子结点。