素数环问题
问题描述
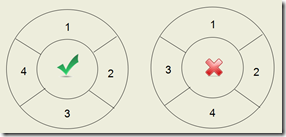
把从1到n(n>=2)这n个数摆成一个环,要求相邻的两个数的和是一个素数,找出所有满足条件的环。
问题分析
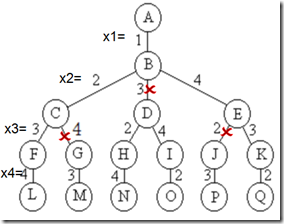
1> 解向量:<x1, x2, ··· , xn>
2> 解空间树:排列树,(n-1)!个叶子结点
3> 剪枝函数:isPrime( x[t-1]+x[t] ),t=2,3,···,n 约束函数
算法实现
#include <iostream>
#include <cmath>
using namespace std;
int n; // 素数环中数字个数
int sum = 0; // 可行方案数
int x[101]; // x数组存放素数环
void backtrack(int t);
bool isPrime(int m);
void main()
{
cout << "请输入素数环中数字的个数:";
while (cin >> n)
{
sum = 0;
for (int i=1; i<=n; i++)
{
x[i] = i;
}
backtrack(2); // 素数环中第一个数为1,从第二个数开始递归求解
cout << "可行方案数为" << sum << endl;
cout << "----------------------------" << endl;
cout << "请输入素数环中数字的个数:";
}
}
/* 回溯法 排列树 */
void backtrack(int t)
{
if (t > n) // 搜索至叶子结点
{
if (isPrime(x[n]+x[1]))
{
sum ++;
// 输出当前方案
for (int i=1; i<=n; i++)
{
cout << x[i] << " ";
}
cout << endl;
}
}
else
{
for (int i=t; i<=n; i++) // 排列树
{
swap(x[t], x[i]);
if (isPrime(x[t-1]+x[t])) // 约束函数
{
backtrack(t+1);
}
swap(x[t], x[i]);
}
}
}
// 判断是否为素数
bool isPrime(int m)
{
int k = (int)sqrt(m);
for(int i=2; i<=k; i++)
{
if(m%i == 0)
{
return false;
}
}
return true;
}
程序执行结果: