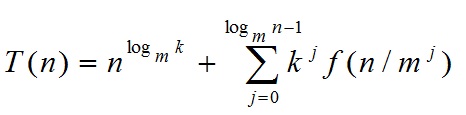递归与分治策略

hello 你好放松放松发顺丰的说法都是付水电费水电费的说法适当放松的方式水电费水电费水电费时代发生的付水电费水电费水电费地方发送到水电费水电费算法水电费水电费算法速度付水电费速度付水电费水电费算法水电费水电费水电费沙发上地方是水电费水电费水电费水电费算法算法水电费杀毒分水电费杀毒付水电费算法水电费算法水电费算法算法水电费是方式发送到 是非颠倒

基本思想

分治法的基本思想是，将一个难以直接解决的大问题，分割成一些规模较小的子问题，这些子问题互相独立且与原问题相同。递归地解这些子问题，然后将各子问题的解合并得到原问题的解。（分-治-合）

适用条件

分治法所能解决的问题一般具有以下几个特征：

• 该问题的规模缩小到一定的程度就可以容易地解决；
• 该问题可以分解为若干个规模较小的相同问题，即该问题具有最优子结构性质（当问题的最优解包含了其子问题的最优解时，称该问题具有最优子结构性质）；
• 分解出的子问题的解可以合并为原问题的解；
• 分解出的各个子问题是相互独立的。

基本步骤

divide-and-conquer(P)
{
	if ( |P| <= n0 ) { y= adhoc(P);  return y; }	//解决小规模的问题
        else
	{
		divide P into smaller subinstances P1,P2,...,Pk; //分解问题
		for (i=1,i<=k,i++)
			yi=divide-and-conquer(Pi);  //递归的解各子问题
		return merge(y1,...,yk);	//将各子问题的解合并为原问题的解
	}  
}

在用分治法设计算法时，最好使子问题的规模大致相同。即将一个问题分成大小相等的k个子问题的处理方法是行之有效的。这种使子问题规模大致相等的做法是出自一种平衡(balancing)子问题的思想。

复杂性分析

一个分治法将规模为n的问题分成k个规模为n／m的子问题去解。设分解阀值n0=1，且adhoc解规模为1的问题耗费1个单位时间。再设将原问题分解为k个子问题以及用merge将k个子问题的解合并为原问题的解需用f(n)个单位时间。用T(n)表示该分治法解规模为|P|=n的问题所需的计算时间，则有： 通过迭代法求得方程的解：