【笔记】【数据结构】【堆】配对堆(合并堆)
资料来源 OI-wiki
配对堆:
(1)配对堆是一棵带权多叉树,其权值满足堆性质(即每个节点的权值都小于他的所有儿子)。

通常我们使用左儿子右兄弟表示法储存一个配对堆(如下图),从下文可以看出这种方式可以方便配对堆的实现。

各项操作的实现
存储结构定义
就是普通的带权多叉树的表示方式。
struct Node { T v; // T为权值类型 Node *ch, *xd; // ch为该节点儿子的指针,xd为该节点兄弟的指针。 //若该节点没有儿子/兄弟则指针指向空节点 nullptr。 };
查询最小值
直接返回根节点、
合并
直接把根节点权值较大的那个配对堆设成另一个的儿子就好。
复杂度:O(1)
Node* merge(Node* a, Node* b) { // 若有一个为空则直接返回另一个 if (a == nullptr) return b; if (b == nullptr) return a; if (a->v > b->v) swap(a, b); // swap后a为权值小的堆,b为权值大的堆 // 将b设为a的儿子 b->xd = a->ch; a->ch = b; return a; }
插入
将插入的元素,视作一个配对堆即可。
删除最小值
删除最小值是配对堆最重要的(也是最复杂)的一个操作。
考虑我们拿掉根节点之后会发生什么,根节点原来的所有儿子构成了一片森林,所以我们要把他们合并起来。
一个很自然的想法是使用 merge 函数把儿子们一个一个并在一起,这样做的话正确性是显然的,但是会导致复杂度退化到 。为了保证删除操作的均摊复杂度为 ,我们需要:
把儿子们 从左往右 两两配成一对,用 merge 操作把被配成同一对的两个儿子合并到一起(见下图 1),再将新产生的堆 从右往左 暴力合并在一起(见下图 2)。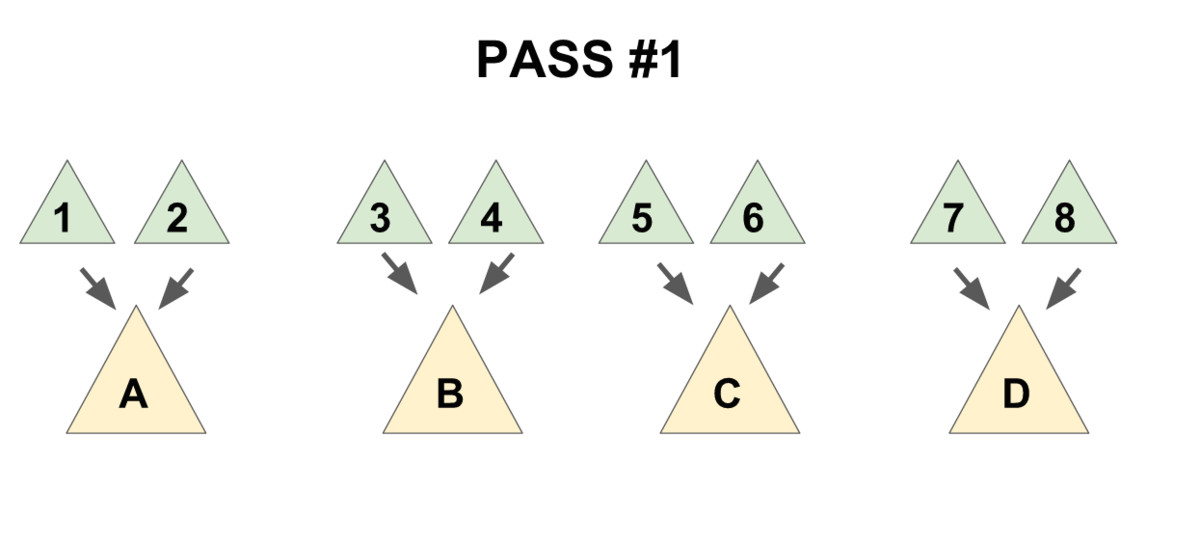
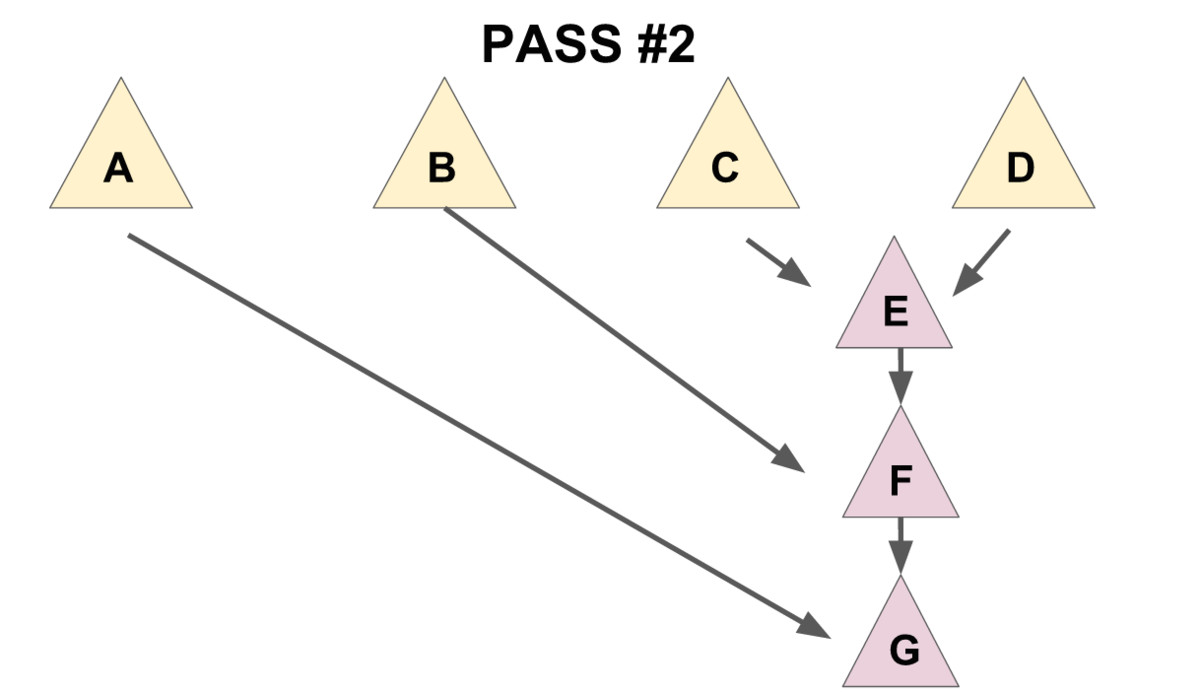
先实现一个辅助函数 merges,作用是合并一个节点的所有兄弟。
Node* merges(Node* x) { if (x == nullptr || x->xd == nullptr) return x; // 如果该树为空或他没有兄弟(即他的父亲的儿子数小于2),就直接return。 Node *a = x->xd, *b = a->xd; // a:x的一个兄弟,b:x的另一个兄弟 x->xd = a->xd = nullptr; // 拆散 return merge(merge(x, a), merges(b)); // 核心部分 }
merge(x,a)“配对”了 x 和 a。最后一句话是该函数的核心,这句话分三部分:
merges(b)递归合并 b 和他的兄弟们。- 将上面 2 个操作产生的 2 个新树合并。
需要注意到的是,上文提到了配对方向和合并方向是有要求的(从左往右配对,从右往左合并),该递归函数的实现已保证了这个顺序,如果读者需要自行实现迭代版本的话请务必注意保证该顺序,否则复杂度将失去保证。
有了 merges 函数,delete-min 操作就显然了。(因为这个封装实在没啥用,实际在实现时中一般不显式写出这个函数)
Node* delete_min(Node* x) { return merges(x->ch); }
减小一个元素的值
要实现这个操作,需要给节点添加一个 father 指针,其指向前一个节点而非树形结构的父节点。
首先节点的定义修改为:
struct Node { T v; Node *ch, *xd; Node *fa; // 新增:fa指针,指向该节点的父亲,若该节点为根节点则指向空节点 // nullptr };
merge 操作修改为:
Node* merge(Node* a, Node* b) { if (a == nullptr) return b; if (b == nullptr) return a; if (a->v > b->v) swap(a, b); a->fa = nullptr; b->fa = nullptr; // 新增:维护fa指针 b->xd = a->ch; if (a->ch != nullptr) // 判断a的子节点是否为空 否则会空指针异常 a->ch->fa = b; a->ch->fa = b; // 新增:维护fa指针 a->ch = b; return a; }
merges 操作修改为:
Node* merges(Node* x) { x->fa = nullptr; // 新增:维护fa指针 if (x == nullptr || x->xd == nullptr) return x; Node* a = x->xd; Node* b = nullptr; if (a != nullptr) { b = a->xd; x->xd = a->xd = nullptr; } else { x->xd = nullptr; } a->fa = nullptr; // 新增:维护fa指针 return merge(merge(x, a), merges(b)); }
现在我们来考虑如何实现 decrease-key 操作。
// root为堆的根,x为要操作的节点,v为新的权值,调用时需保证x->v>=v // 返回值为新的根节点 Node* decrease - key(Node* root, Node* x, LL v) { x->v = v; // 修改权值 if (x->fa == nullptr) return x; // 如果x为根,就不用接下去的步骤了。 // 把x从fa的子节点中剖出去,这里要分x的位置讨论一下。 if (x->fa->ch == x) x->fa->ch = x->xd; else x->fa->xd = x->xd; x->xd->fa = x->fa; x->xd = nullptr; x->fa = nullptr; return merge(root, x); // 合并root和x。 }
首先我们发现,当我们对节点 x 进行 decrease-key 操作后,以 x 为根的子树仍然满足配对堆性质,但 x 的父亲和 x 之间可能不再满足堆性质。
因此我们可以把整棵以 x 为根的子树剖出来,这样现在两棵树都符合配对堆性质了,再把他们 merge 起来就做完了。
通常可以简单的认为复杂度为 o(logn)(注意这里为小 o)。
例题:洛谷-左偏树模板
#include<bits/stdc++.h> using namespace std; int n,m; const int N=1e5+10; int d[N]; vector <int > son[N]; int fa[N]; int find(int x) { if(!fa[x] ) return x; else return fa[x]=find(fa[x]); } int merge(int a,int b) { if(a==b ) return a; if(a>b ) swap(a,b);//因为题目对删除哪个堆的序号有要求,所以先固定序号顺序 if(d[a] <= d[b] ) return fa[b]=a,son[a].push_back(b),a; else return fa[a]=b,son[b].push_back(a),b; } bool broken[N]; void del(int x) { if(broken[x] ) { printf("-1\n"); return ; } x=find(x); printf("%d\n",d[x]); broken[x]=true; queue <int> s; int sz=son[x].size() ; for(int i=0;i<sz;i++) { int t=son[x][i];//del操作流程: fa[t]=0; //全部变成一个个独立的堆,然后删除老根,然后合并这些新出现的堆 s.push(t); } son[x].clear() ; while( (sz--)>1 )//当队列中有超过一个元素时,去删除一个元素 { int a=s.front();s.pop(); int b=s.front();s.pop(); s.push( merge(a,b) ); } if( !s.empty() ) fa[x]=s.front();//1就算x被删除了,通过路径压缩,要将那些fa指向x的点,指向新的根!!!防止一些点迷路了 } int op,u,v; int main() { scanf("%d%d",&n,&m); for(int i=1;i<=n;i++) scanf("%d",&d[i]); while(m--) { scanf("%d%d",&op,&u); if(op==1) { scanf("%d",&v); if(!broken[u] && !broken[v] ) merge(find(u),find(v)); } else if(op==2 ) del(u); } return 0; }


