Codeforces Round #565 (Div. 3) E. Cover it!
Codeforces Round #565 (Div. 3)
You are given an undirected unweighted connected graph consisting of n vertices and m edges. It is guaranteed that there are no self-loops or multiple edges in the given graph.
Your task is to choose at most ⌊n2⌋ vertices in this graph so each unchosen vertex is adjacent (in other words, connected by an edge) to at least one of chosen vertices.
It is guaranteed that the answer exists. If there are multiple answers, you can print any.
You will be given multiple independent queries to answer.
Input
The first line contains a single integer t (1≤t≤2⋅105) — the number of queries.
Then t queries follow.
The first line of each query contains two integers n and m (2≤n≤2⋅105, n−1≤m≤min(2⋅105,n(n−1)2)) — the number of vertices and the number of edges, respectively.
The following m lines denote edges: edge i is represented by a pair of integers vi, ui (1≤vi,ui≤n, ui≠vi), which are the indices of vertices connected by the edge.
There are no self-loops or multiple edges in the given graph, i. e. for each pair (vi,ui) there are no other pairs (vi,ui) or (ui,vi) in the list of edges, and for each pair (vi,ui) the condition vi≠ui is satisfied. It is guaranteed that the given graph is connected.
It is guaranteed that ∑m≤2⋅105 over all queries.
Output
For each query print two lines.
In the first line print k (1≤⌊n2⌋) — the number of chosen vertices.
In the second line print k distinct integers c1,c2,…,ck in any order, where ci is the index of the i-th chosen vertex.
It is guaranteed that the answer exists. If there are multiple answers, you can print any.
Example
input
2
4 6
1 2
1 3
1 4
2 3
2 4
3 4
6 8
2 5
5 4
4 3
4 1
1 3
2 3
2 6
5 6
output
2
1 3
3
4 3 6
Note
In the first query any vertex or any pair of vertices will suffice.
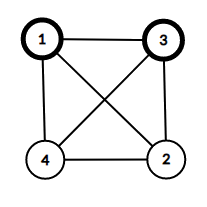
Note that you don't have to minimize the number of chosen vertices. In the second query two vertices can be enough (vertices 2 and 4) but three is also ok.
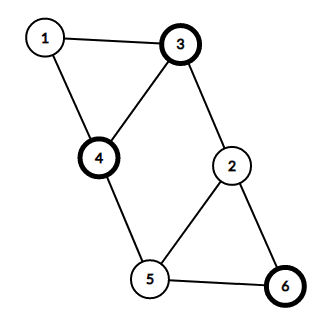
题意:选取不多于n/2个点,使所有点都被连接......
思路:用dfs染色,相邻点染成1或者2,最后遍历一遍color数组,看1和2谁小于等于二分之n,就输出谁......
1 #include<iostream>
2 #include<cstring>
3 #include<cstdio>
4 #include<cmath>
5 #include<algorithm>
6 #include<map>
7 #include<set>
8 #include<vector>
9 #include<queue>
10 using namespace std;
11 #define ll long long
12 const int mod=1e9+7;
13 const int inf=1e9+7;
14
15 const int maxn=2e5+10;
16
17 int n,m;
18 int x,y;
19
20 vector<int>v[maxn];
21
22 int color[maxn];
23
24 void dfs(int cur,int Color)
25 {
26 color[cur]=Color;
27
28 int now;
29 if(Color==1)
30 now=2;
31 else
32 now=1;
33
34 for(int i=0;i<v[cur].size();i++)
35 {
36 if(!color[v[cur][i]])
37 {
38 dfs(v[cur][i],now);
39 }
40 }
41
42 }
43
44 int main()
45 {
46 ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
47
48 int T;
49 cin>>T;
50
51 while(T--)
52 {
53 cin>>n>>m;
54
55 for(int i=1;i<=n;i++)
56 {
57 v[i].clear();
58 color[i]=0;
59 }
60
61 for(int i=0;i<m;i++)
62 {
63 cin>>x>>y;
64 v[x].push_back(y);
65 v[y].push_back(x);
66 }
67
68 dfs(1,1);
69
70 int cnt=0;
71 for(int i=1;i<=n;i++)
72 if(color[i]==1)
73 cnt++;
74
75 int flag=0;
76 if(cnt<=n/2)
77 {
78 cout<<cnt<<endl;
79 for(int i=1;i<=n;i++)
80 {
81 if(color[i]==1)
82 {
83 if(!flag)
84 {
85 flag=1;
86 cout<<i;
87 }
88 else
89 cout<<" "<<i;
90 }
91 }
92 }
93 else
94 {
95 cout<<n-cnt<<endl;
96 for(int i=1;i<=n;i++)
97 {
98 if(color[i]==2)
99 {
100 if(!flag)
101 {
102 flag=1;
103 cout<<i;
104 }
105 else
106 cout<<" "<<i;
107 }
108 }
109 }
110 cout<<endl;
111 }
112 return 0;
113 }



