cute 02 layout代数

cute 教程 02 Layout代数

cute 提供layout代数来支持layout的组合，包括如下的一些操作:

Layout 函数复合
Layout product: 将layout reproduce; 简单 -> 复杂
Layout divide: 将layout划分; 划分例如数据的layouts

coalesce

coalesce操作是一个用于函数的简化。

auto layout = Layout<Shape <_2, Shape<_1,_6>>,
    Stride<_1, Stride<_6, _2>>>{};
auto result = coalesce(layout); // _12: _1

简单理解就是原先，我们一般会给一个自然坐标，例如(0,0,2)，这个自然坐标实际上对应了一个1D坐标，这里的转换就是将这种直接转为单个数字。

我们可以讨论一下只有两个整型mode的layout，即s0:d0 ++ s1:d1.有四种情况:

s0:d0 ++ _1:d1 => s0:d0
_1:d0 ++ s1:d1 => s1:d1
s0:d0 ++ s1:s0*d0 => s0*s1:d0
s0:d0 ++ s1:d1 => (s0, s1):(d0:d1)

by-mode coalesce

有时我们也会关注layout的形状，但是仍然想coalesce；例如对于一个2D的layout，我们想让其结果仍然为2D。

由于这个原因，coalease存在一个额外参数的重载

Layout coalesce(Layout const& layout, IntTuple const& trg_profile);

// usage
auto a = Layout<Shape <_2,Shape <_1,_6>>,
                Stride<_1,Stride<_6,_2>>>{};
auto result = coalesce(a, Step<_1,_1>{});   // (_2,_6):(_1,_2)
// Identical to
auto same_r = make_layout(coalesce(layout<0>(a)),
                          coalesce(layout<1>(a)));

注意我们可以理解这里的Step<_1, _1>{}仅仅作为flag，它的值并不起作用。

Composition

Layout的复合是cute的核心，几乎在每个核心操作都有应用。

我们可以从layout的本质是从整数到整数的映射触发，定义如下的函数复合，一个例子如下:

首先可以定义函数复合 A . B
R(c) := (A . B)(c) := A(B(c))

例子
A = (6,2):(8,2)
B = (4,3):(3,1)

R(0) = A(B(0)) = A(B(0,0)) = A(0) = A(0,0) = 0

我们可以惊讶地发现这个R也可以使用一个layout表示

R = ((2,2),3):((24,2),8)

// 并且
compatible(B, R) // -> cute 01 
// B 的shape 与R的shape兼容
// 1. size一致
// 2. B中有效的坐标在R中也有效

这个性质是我们想要的，因为B实际上定义了复合函数的domain，即定义域。

我们可以看下layout复合的测试方法

// @post compatible(@a layout_b, @a result)
// @post for all i, 0 <= i < size(@a layout_b), @a result(i) == @a layout_a(@a layout_b(i)))
Layout composition(LayoutA const& layout_a, LayoutB const& layout_b)

复合的计算

首先，我们有如下几个观察:

B = (B_0, B_1, ...). 1个layout可以表示为它的sublayout的连接操作
A o B = A o (B_0, B_1, ...) = (A o B_0, A o B_1, ...). 当B是injective的，复合对于连接是左分配律的。

我们假设B = s:d，如果A = a:b，那么复合是平凡的 R = A o B = s:b*d. 但如果A是多个mode，那么就需要认真考虑。

我们可以不考虑这个具体怎么推导，从直观上理解。

Layout a = make_layout(make_shape (Int<10>{}, Int<2>{}),
                       make_stride(Int<16>{}, Int<4>{}));
Layout b = make_layout(make_shape (Int< 5>{}, Int<4>{}),
                       make_stride(Int< 1>{}, Int<5>{}));
Layout c = composition(a, b);
print(c);

By-mode 复合

与by-modecoalesce类似并且我们想要表示通用的tiling操作，有时我们需要对一些modes才应用composition。因此，当第二个参数为tiler时，composition将执行by-mode的复合

// (12,(4,8)):(59,(13,1))
auto a = make_layout(make_shape (12,make_shape ( 4,8)),
                     make_stride(59,make_stride(13,1)));
// <3:4, 8:2>
auto tiler = make_tile(Layout<_3,_4>{},  // Apply 3:4 to mode-0
                       Layout<_8,_2>{}); // Apply 8:2 to mode-1

// (_3,(2,4)):(236,(26,1))
auto result = composition(a, tiler);
// Identical to
auto same_r = make_layout(composition(layout<0>(a), get<0>(tiler)),
                          composition(layout<1>(a), get<1>(tiler)));

注意一下记号，我们通常使用<LayoutA, LayoutB, ...>的记号表示tilers，而使用(LayoutA, LayoutB, ...)的记号表示layouts的复合。

tiler的结果如下:

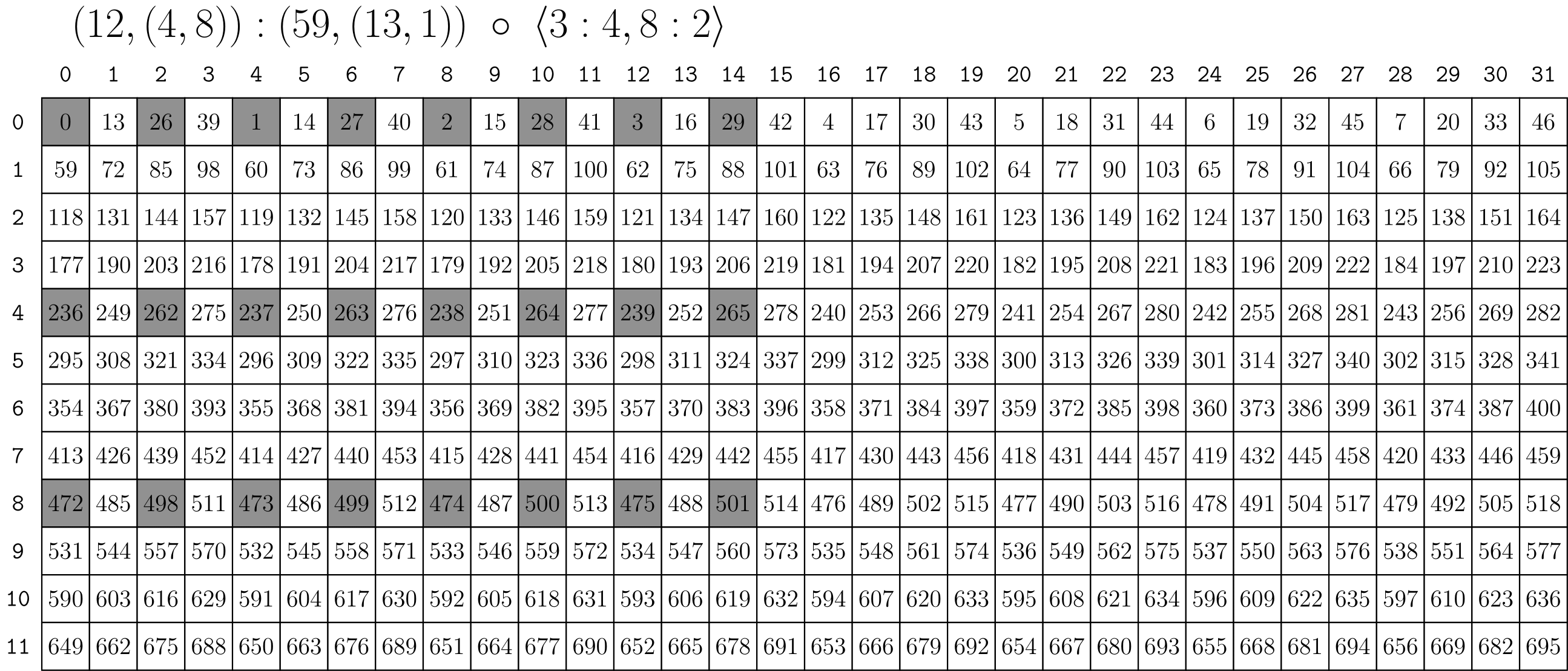
我们可以理解是在一个大的layout下挑选某些元素组成一个layout

为了方便起见，cute也可以将Shape解释为tiler, 一个Shape表示layouts的元组，其中stride为1.

// (12,(4,8)):(59,(13,1))
auto a = make_layout(make_shape (12,make_shape ( 4,8)),
                     make_stride(59,make_stride(13,1)));
// (8, 3)
auto tiler = make_shape(Int<3>{}, Int<8>{});
// Equivalent to <3:1, 8:1>
// auto tiler = make_tile(Layout<_3,_1>{},  // Apply 3:1 to mode-0
//                        Layout<_8,_1>{}); // Apply 8:1 to mode-1

// (_3,(4,2)):(59,(13,1))
auto result = composition(a, tiler);

结果如下：

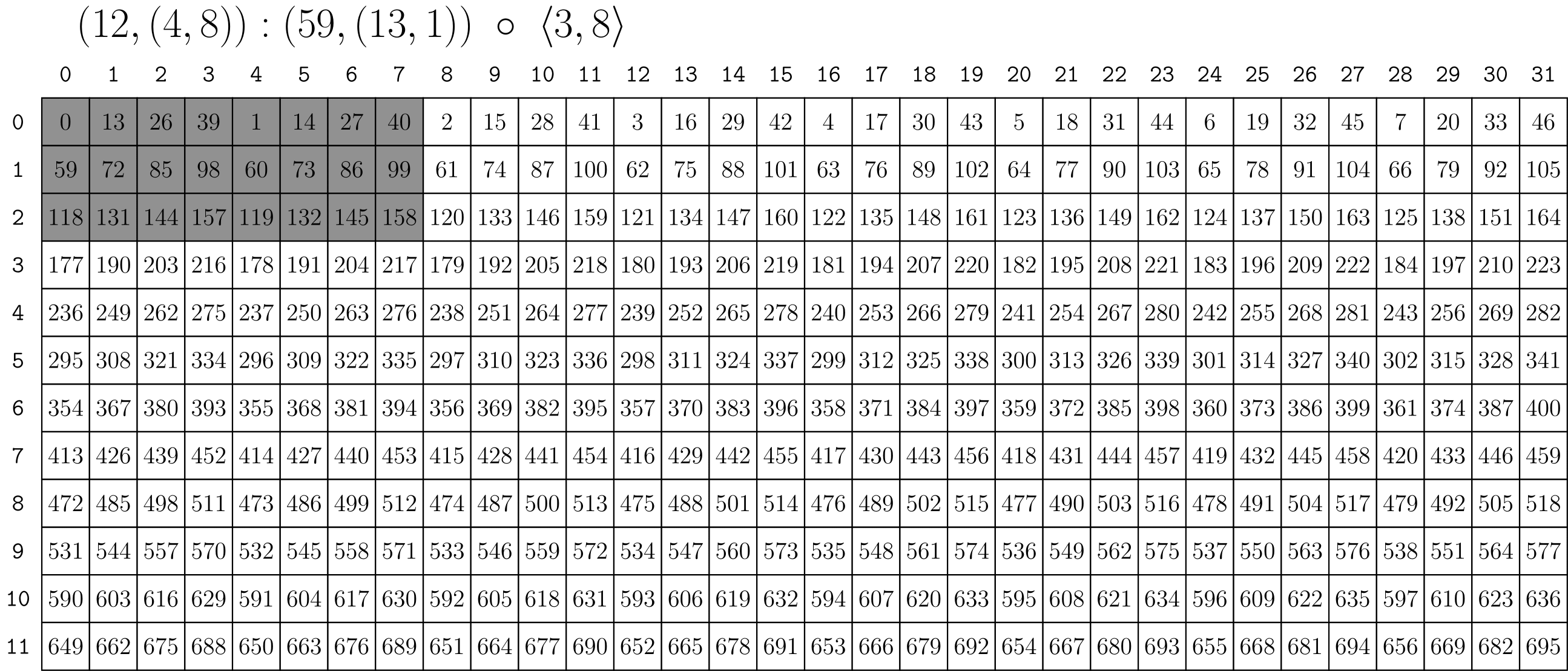
复合中的tilers

一个tiler可以是下列对象之一:

一个layout
tilers的元组
一个shape

上述任何一个都可以作为composition的第二个参数。

complement

在我们讨论product和divide之前，我们还需要更多的操作。为了实现通用的tiling，我们想挑选任意的元素--作为tile, 以及能描述tiles本身的layout.

Layout complement(Layout const& layout_a, Shape const& cotarget);

layoutA关于ShapeM的complementR遵循以下性质:

R的size以及cosize受限于size(M).
R是有序的，即R的strides是正的，以及递增的。
A和R有不相交的codomain, R尝试完成A的codmain。

cotarget参数最常见的是一个int--你可以看到我们只使用size(cotarget). 然而有时指定一个静态的int是有用的;例如28是一个动态int，而(_4,7)则是一个size为28的shape，其中我们静态的指导可以被_4除。两者都会产生相同的complement，但是额外的信息可以被complement使用来维护结果的静态性。

例子

complement在静态shapes和strides上更有效率, 所以应该考虑所有int尽可能静态。

可视化例子如下:

除法(tiling)

最后我们可以定义Layout之间的除法

logical_divide(Layout, Layout)

auto logical_divide(Layout<LShape, LSride> const& layout,
    Layout<TShape, TSride> const& tiler) {
        return composition(layout, make_layout(tiler, complement(tiler, size(layout))));
    }

直观上理解，是将某个layout按照tiler进行划分，结果中的第一个mode表示tiler的layout，第二个则表示某个补。

一个1D的例子如下:

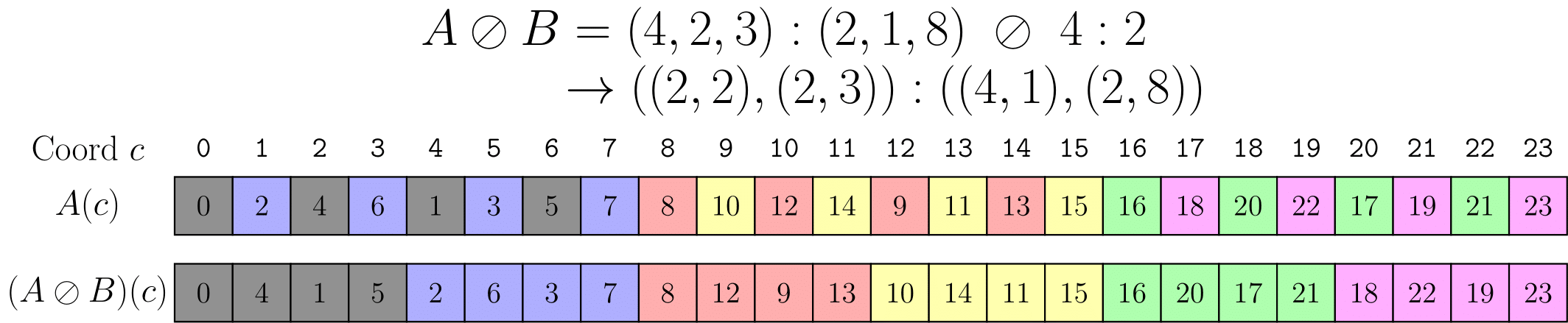
2D的例子如下:

zipped, tiled, flat divides

Layout Shape : (M, N, L, ...) 
Tiler Shape  : <TileM, TileN>


logical_divide : ((TileM,RestM), (TileN,RestN), L, ...)
zipped_divide  : ((TileM,TileN), (RestM,RestN,L,...))
tiled_divide   : ((TileM,TileN), RestM, RestN, L, ...)
flat_divide    : (TileM, TileN, RestM, RestN, L, ...)

logical_divide相当于对每个mode都除一下，tile存放在各个维度中；zipped是将tile都放在一块；tiled是将后面的mode直接拆包；而flat直接就全部解包。

Product

我们经常使用

blocked_product(LayoutA, LayoutB)

raked_product(LayoutA, LayoutB)

来进行表示，这里的参数都是layout，而没有tiler；这会更加直观。例子如下:

Layout Shape : (M, N, L, ...)
Tiler Shape  : <TileM, TileN>

logical_product : ((M,TileM), (N,TileN), L, ...)
zipped_product  : ((M,N), (TileM,TileN,L,...))
tiled_product   : ((M,N), TileM, TileN, L, ...)
flat_product    : (M, N, TileM, TileN, L, ...)

posted @ 2025-03-27 20:27 xwher 阅读(50) 评论(0) 收藏举报

刷新页面返回顶部

xwher