并查集详解+模板

　　并查集，顾名思义，就是一个合并和查询的过程，其实际意义类似于等价划分的作用（划分出不同的等价类）。掌握基本的知识和思想后，便可以运用并查集来解决问题。其中，学会使用并查集的模板对解决并查集问题十分十分有帮助。

 

并查集：(union-find sets)

　　一种简单的用途广泛的集合. 并查集是若干个不相交集合，能够实现较快的合并和判断元素所在集合的操作，应用很多，如其求无向图的连通分量个数等。最完美的应用当属：实现Kruskar算法求最小生成树。

 并查集的精髓（即它的三种操作，结合实现代码模板进行理解）：

1、Make_Set(x) 把每一个元素初始化为一个集合

初始化后每一个元素的父亲节点是它本身，每一个元素的祖先节点也是它本身（也可以根据情况而变）。

2、Find_Set(x) 查找一个元素所在的集合

查找一个元素所在的集合，其精髓是找到这个元素所在集合的祖先！这个才是并查集判断和合并的最终依据。
判断两个元素是否属于同一集合，只要看他们所在集合的祖先是否相同即可。
合并两个集合，也是使一个集合的祖先成为另一个集合的祖先，具体见示意图

3、Union(x,y) 合并x,y所在的两个集合

合并两个不相交集合操作很简单：
利用Find_Set找到其中两个集合的祖先，将一个集合的祖先指向另一个集合的祖先。如图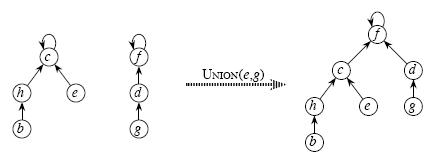

 

并查集的优化

1、Find_Set(x)时 路径压缩
寻找祖先时我们一般采用递归查找，但是当元素很多亦或是整棵树变为一条链时，每次Find_Set(x)都是O(n)的复杂度，有没有办法减小这个复杂度呢？
答案是肯定的，这就是路径压缩，即当我们经过"递推"找到祖先节点后，"回溯"的时候顺便将它的子孙节点都直接指向祖先，这样以后再次Find_Set(x)时复杂度就变成O(1)了，如下图所示；可见，路径压缩方便了以后的查找。

 

2、Union(x,y)时 按秩合并
即合并的时候将元素少的集合合并到元素多的集合中，这样合并之后树的高度会相对较小。

实现代码：

int par[100];　　//par[i]代表i的父结点
int rank[100];    //rank[i]代表i结点所在树的高度

void init(){    //初始化
    for(int i=1;i<=n;i++){
        par[i]=i;
        rank[i]=0;            //高度最初为0 
    }
}

int find(int x){    //查询根
    if(par[x]==x){
        return x;
    }else return par[x]=find(par[x]);
}

void unite(int x,int y){    //合并
    x=find(x);
    y=find(y);
    if(x==y)    return;
    
    if(rank[x]<rank[y]){
        par[x]=y;
    }else{
        par[y]=x;
        if(rank[x]==rank[y]){
            rank[x]++;            //高度加1 
        }
    }
}

bool same(int x,int y){  //判断是否同类
    return find(x)==find(y);
}       

 文章参考来源：

https://www.cnblogs.com/cherish_yimi/archive/2009/10/11/1580839.html