分治——最近点对问题

最近点对问题：

在平面内有点集 S ，S 包含 n 个点。已知每个点的坐标 (x, y) ，求最近的两点之间的距离（ n > 2）。如果存在重合的两个点，最近距离记为0。

枚举的方法时间复杂度是 O(n^2) ，通过分治可以将时间复杂度降为 O(nlog(n))；

分治策略

​ 利用一条直线将平面上的所有点集 S 分成两部分S1、S2，分别计算这两部分的最短距离d1、d2，再进行合并。合并时，平面上所有点的最短距离为 dis，则 dis 就是 d1、d2 和分别在位于S1 和 S2 的两个点对的距离 d12 中最小的那个，即：dis = Closest() = min (d1, d2, d12);

算法描述

首先需要对将 S 中所有点存放在结构体数组 points[ ] 中（共有 n 个），按照 x 坐标的大小将 points[ ] 从小到大进行排序。其中结构体包含点的 x 坐标和 y 坐标。

求最近点距 dis = Closest(1, n) ，有划分、递归、合并三个基本步骤。

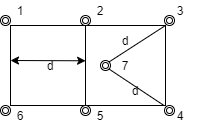
1. 划分：取排序的中间位置处的一条直线 mid = l + r，将平面分成左右两部分S1，S2 如图。

   

2. 递归：递归调用求最近点距函数 Closest( ) ，分别计算 S1 和 S2 两个点集的最短距 d1 和 d2。取 d1 和 d2 中较小的那个作为 d 。

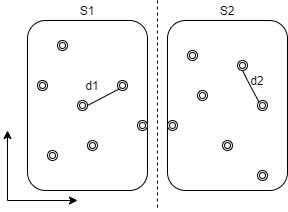
3. 合并：计算分别位于 S1 和 S2 的两个点之间最小的距离 d12。对于 x < mid - d 或者 x > mid + d 范围内的点，显然不会出现点距小于 d 的情况。因此只需要在 mid 左右为 d 的范围内寻找最近的点距。有以下步骤：

   1. 将处于 mid - d <= x <= mid + d 范围内的点选出来，存储到 selected[ ] 数组中，selected[ ] 数组是一个临时数组，用来存放选出来的点的索引。

   

   2. 将 selected[ ] 按照 y 坐标的值从小到大排序。目的是将 y 方向距离比较近的点放在一起。遍历selected[] 数组中的点时，对于每个点最多遍历出现在它下面相邻的 6 个点，因此合并是线性复杂度。
   3. 最终的最小点距 dis = min(d1, d2, d12)

”最多遍历6个其他点“ 解释：

​ 对于 selected[ ] 数组中的每个点，只需要遍历其下方的点，因为它上方点遍历其他点的时候已经把它们之间的距离计算过了，所以只需要考虑下方距离为 d ，左右距离也分别为 d 的矩形区域，如下图。不妨把 mid 线上的点认为属于S1，那么由于左侧正方形区域中最近距离为 d1 ( < d )， 所以左边正方形最多存在1、2、5、6 四个点，如果有第5个点，那就一定会有该点与某个点的距离小于 d1 与左侧最小距离为 d1 矛盾。除 mid 线上的两个点外（已经算在左侧区域中），右侧最多包含3、4、7三个点，其中 7 是分别以3、4为圆心 d2 为半径的圆弧的交点。所以这个矩形区域内，对于某个遍历到的点，最多计算它与其他6个点之间的距离

复杂度分析

递归深度是 log(n) ,每次递归的时间复杂度是 nlog(n)（有排序），所以复杂度是 $$O(nlog(n)log(n))$$

代码示例

#include <cstdio>
#include <math.h>
#include <algorithm>
#define MAX 100002
#define INF 1e30
using namespace std;
struct Point
{
    double x, y;
} points[MAX];
int selected[MAX]; 
bool cmp1(const Point &a, const Point &b)
{
    return a.x < b.x;
}

bool cmp2(const int &a, const int &b)
{
    return points[a].y < points[b].y;
}

// 计算两个点之间的距离
double len(const int &a, const int &b)
{
    return sqrt((points[a].x - points[b].x) * (points[a].x - points[b].x) + 
                (points[a].y - points[b].y) * (points[a].y - points[b].y));
}

// 计算最近点距
double Closest(int l, int r)
{
    if (l == r)
        return INF;
    if (l + 1 == r)
        return len(l, r);
    double min;
    int mid = (l + r) / 2;
    /* 计算分隔线同侧点对的最短距离 */
    double leng1 = Closest(l, mid);
    double leng2 = Closest(mid + 1, r);
    leng1 < leng2 ? min = leng1 : min = leng2;
    /* 计算分隔线两侧点对的距离 */
    int j = 0;
    // 找出所有离分隔线的距离小于min的点
    for (int i = l; i <= r; i++)
    {
        if (points[i].x - points[mid].x >= -min && points[i].x - points[mid].x <= min)
        {
            selected[j] = i;
            j++;
        }
    }
    // 把选出来的点，按照y排序
    sort(selected, selected + j, cmp2);
    // 对于y方向的相距小于min的点，测量距离，更新min
    for (int i = 0; i < j; i++)
    {
        for (int k = i + 1; k < i + 7; k++) // 最多遍历6个其他点
        {
            if (points[selected[k]].y - points[selected[i]].y > min)
                break;
            double temp = len(selected[i], selected[k]);
            if (temp < min)
                min = temp;
        }
    }
    return min;
}

int main(int argc, char const *argv[])
{
    int n;
    while (true)
    {
        scanf("%d", &n);
        if (n == 0)
            break;
        for (int i = 0; i < n; i++)
        {
            scanf("%lf %lf", &points[i].x, &points[i].y);
        }
        sort(points, points + n, cmp1);
        printf("%.2lf\n", Closest(0, n - 1));
    }
    return 0;
}