812. Largest Triangle Area--Easy

You have a list of points in the plane. Return the area of the largest triangle that can be formed by any 3 of the points.

Example:
Input: points = [[0,0],[0,1],[1,0],[0,2],[2,0]]
Output: 2
Explanation:
The five points are show in the figure below. The red triangle is the largest.

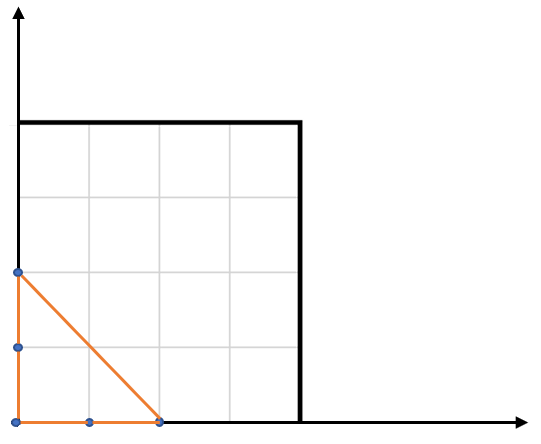
Notes:

3 <= points.length <= 50.
No points will be duplicated.
-50 <= points[i][j] <= 50.
Answers within 10^-6 of the true value will be accepted as correct.

1.思考
(1) 方法1

• 一般计算三角形面积的公式有:底*高/2，但是在本题中，计算高较为困难；
• 通过三点的坐标最直接能够计算出的是三角形三条边的长度，因此使用公式：p = (a+b+c)/2, s = sqrt( p*(p-a)*(p-b)*(p-c) ) = 1/4*sqrt( (a+b+c)(a+b-c)(a-b+c)(-a+b+c) );
  (2) 方法2
• 在提交的某个参考代码中看出了另一种性能更好的方法，并通过数学证明的方法验证了该方法的正确性；
• 示意图如下所示，假设组成三角形的三个顶点为I、J、K，下面我们将证明S△IJK=S△IBK+S△IAJ；
• 因为AC:BC=AK:BJ，即ACBJ=BCAK，所以S△BCK=S△ACJ，得证。
  
  

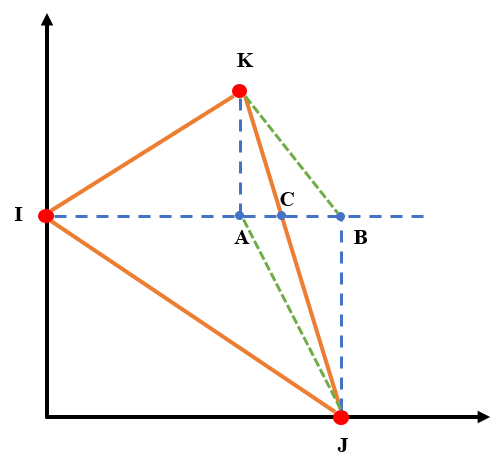
2.实现
(1) 方法1
Runtime: 12ms(47.50%)
Memory: 9.1MB(75.00%)
(2) 方法2
Runtime: 4ms(98.04%)
Memory: 9MB(100%)

//Solution 1
class Solution {
public:
    double largestTriangleArea(vector<vector<int>>& points) {
        int len = points.size();
        double a, b, c;
        double s, res = 0, m;
        for(int i=0; i<len-2; i++){
            for(int j=i+1; j<len-1; j++){
                for(int k=j+1; k<len; k++){
                    a = sqrt(pow(points[i][0]-points[j][0],2)+pow(points[i][1]-points[j][1],2));
                    b = sqrt(pow(points[i][0]-points[k][0],2)+pow(points[i][1]-points[k][1],2));
                    c = sqrt(pow(points[k][0]-points[j][0],2)+pow(points[k][1]-points[j][1],2));
                    s = (a+b+c)/2.0;
                    m = sqrt(s*(s-a)*(s-b)*(s-c));
                    if(m>res)
                        res = m;
                }
            }    
        }        
        return res;        
    }
};

//Solution 2
class Solution {
public:
    inline double abs(double a){return a>0?a:(-a);}    
    double largestTriangleArea(vector<vector<int>>& points) {
        int len = points.size();
        double res = 0, m;
        for(int i=0; i<len-2; i++){
            for(int j=i+1; j<len-1; j++){
                for(int k=j+1; k<len; k++){
                    m = 0.5 *abs((points[i][0]-points[j][0])*(points[i][1]-points[k][1])
                                -(points[i][0]-points[k][0])*(points[i][1]-points[j][1]));
                    if(m>res)
                        res = m;
                }
            }    
        }        
        return res;        
    }
};