平衡二叉排序树 - 星梦缘vs惜

公告

平衡二叉排序树

因为二叉树本身就是个递归的概念，所以在构建平衡二叉树的时候，应时刻记得递归这个概念。

同样的序列，因为排序不同，可能会生成不同的二叉排序树，查找效率性对就不一定了，如：1-9这些数字就可以生成下面两种树。

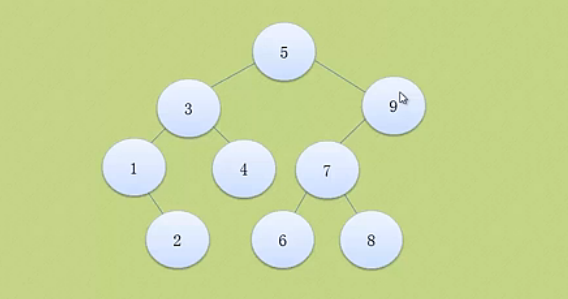
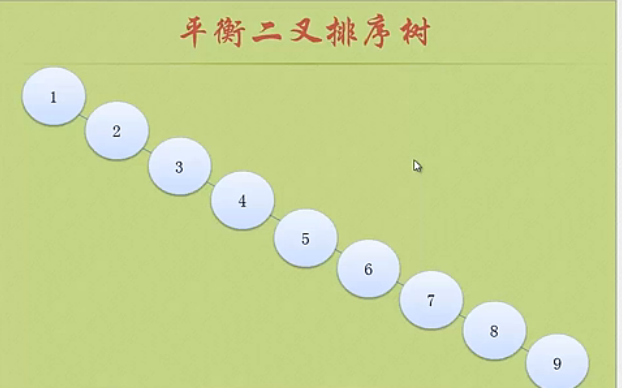
第二种就是一个极端的情况，如果要查找9，就需要进行比较8次，效率很低。由此就引出，平衡二叉树的概念。

什么是平衡二叉树？

希望对一个序列，进行查找，最好的就是将其构建成一个平衡二叉树即AVL树。

但是怎么构建平衡二叉排序树？

前提：必须是一棵树。(类似于：只有先保证他是一个人，才难说他是一个什么样的男人。嘻嘻，这个比喻不是那么准确啦)

下面有一个题目：

怎么将左图构建成右图的平衡二叉树呢？

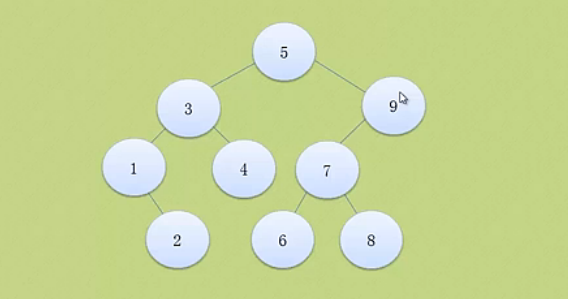
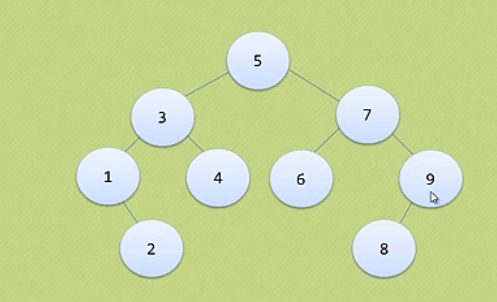
可见，左图和右图的不同就在于是否是平衡的。左图中节点9的平衡因子是2，是个不平衡点。

构造平衡二叉树:

如果在一棵平衡的二叉搜索树中，插入一个新节点时，造成了不平衡。此时必须调整树的结构，使之平衡化。

平衡旋转有两类：

--单旋转(左旋和右旋)

--双旋转(左右旋和右左旋)

每插入一个新节点时，AVL树中相关节点的平衡状态会发生改变。因此，在插入一个新节点后，需要从插入位置沿着通向根的路径回溯，检查各节点的平衡因子。如果在某一节点发现此树不平衡，停止回溯。

从发生不平衡的节点起，沿着刚才回溯的路径取直接下两层的节点。

（1）如果这三个节点处在一条直线上，则采用单旋转进行平衡化。单旋转可按方向分为左单旋转和右单旋转。

（2）如果这三个节点处在一条折线上，则采用双旋转进行平衡化。单旋转可按方向分为先左后右旋转和先右后左旋转。

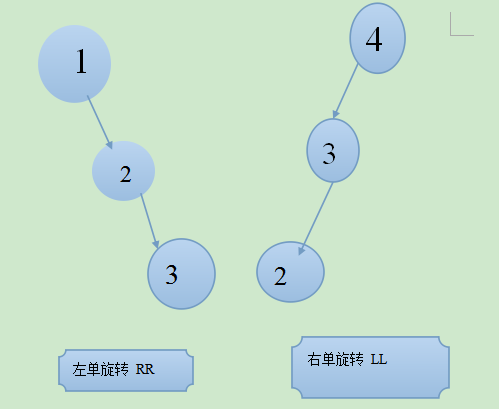
下面举两个简单的例子，便于理解。

1：a[10]={3,2,1,4,5,6,7,10,9,8};对于这压样一个一维数组，构建二叉平衡树。

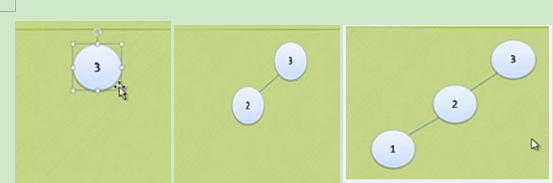
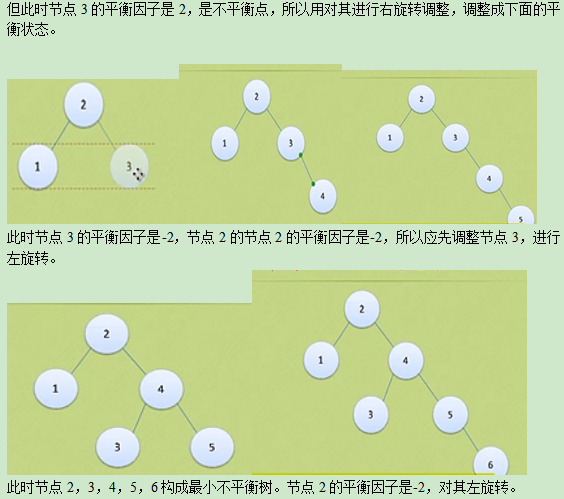
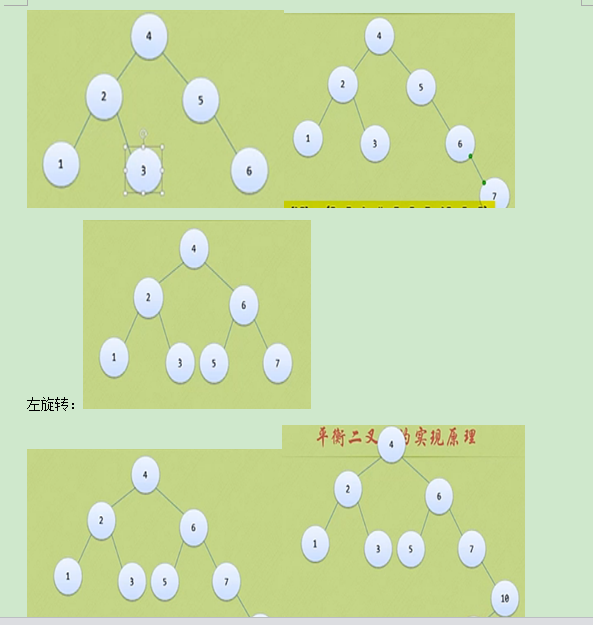
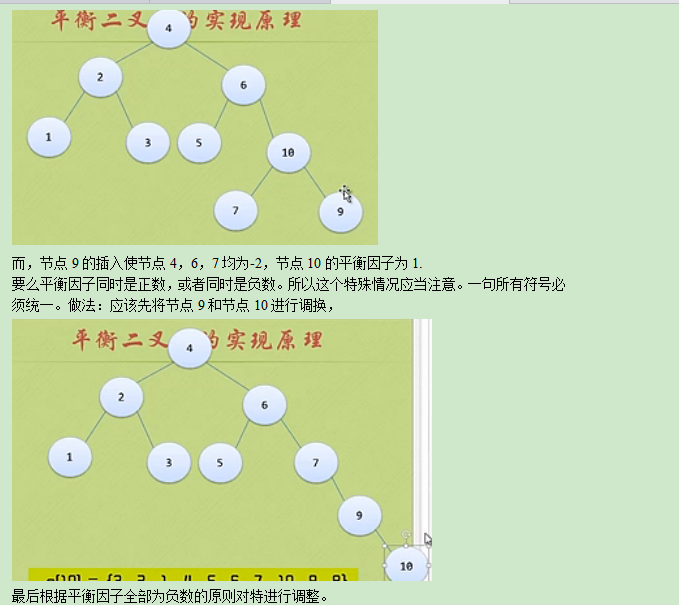
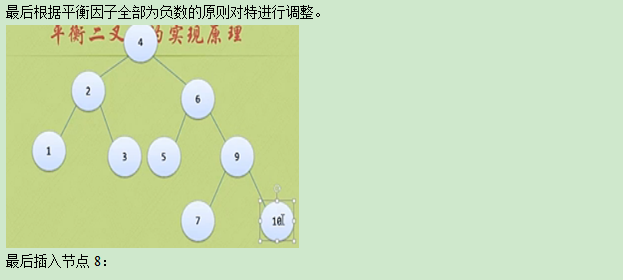
此时构建过程已经完成。

例子2：

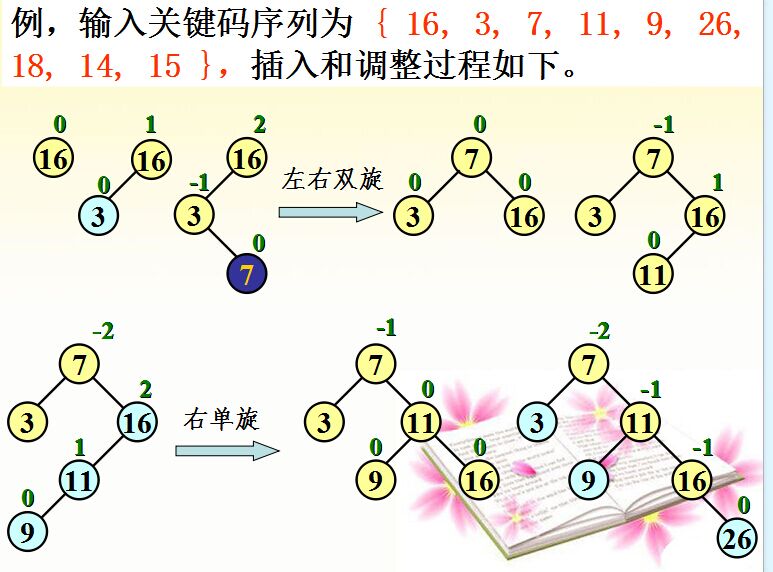
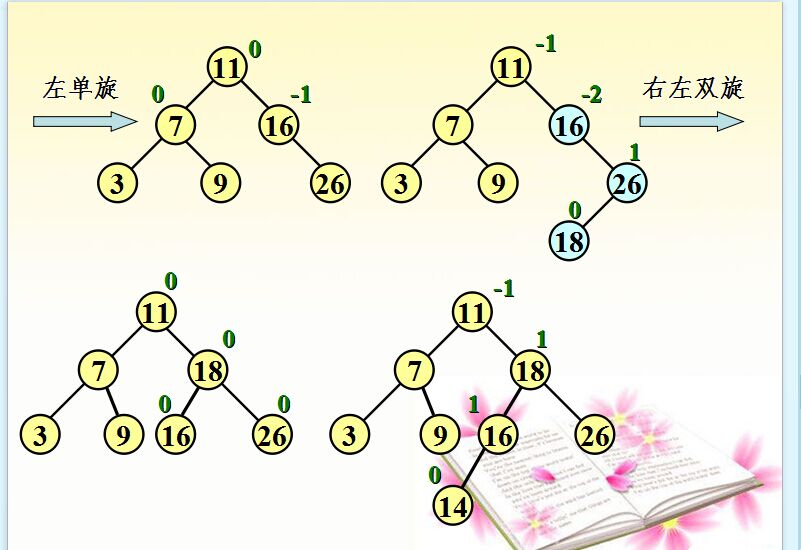
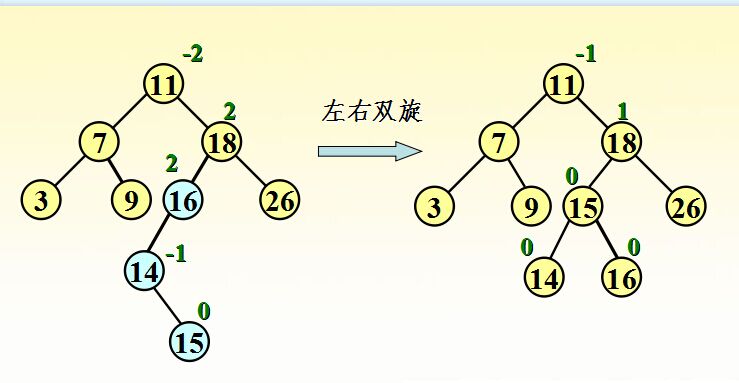
下面是代码实现：

  1 /*平衡二叉树的实现原理
  2   时间：2015-6-21
  3 ***/
  4 #define LH 1//左子树高
  5 #define EH 1//左右子树登高
  6 #define RH 1//右子树
  7 
  8 typedef struct BITNode{
  9   int data;
 10   int bf;
 11   struct BITNode*lchild,*rchild;
 12 }BITNode,*BiTree;
 13 //右旋操作
 14 void R_Rotate(BiTree *p)
 15 {
 16      BiTree L;
 17      L=(*p)->lchild;
 18      (*p)->lchild=L->rchild;
 19      L->rchild=(*p);
 20      *p=L;
 21 }
 22 //左旋操作
 23 void L_Rotate(BiTree *p)
 24 {
 25      BiTree L;
 26      L=(*p)->rchild;
 27      (*p)->rchild=L->lchild;
 28      L->lchild=(*p);
 29      *p=L;
 30 }
 31 //左平衡
 32 void LeftBalance(BiTree *T)
 33 {
 34    BiTree L,lr;
 35    L=(*T)->lchild;
 36    switch(L-bf)
 37    {
 38       case LH;
 39         (*T)->bf=L-bf=EH;
 40          R_RETATE(T)
 41          break;
 42          case RH;
 43           lr=L->rchild;
 44           switch(Lr-bf)
 45          {
 46          case LH;
 47             (*T)->bf=RH;
 48               L->bf=EH;
 49               break;
 50          case EH;
 51              (*T)->bf=L-bf=EH;
 52               break;
 53          case RH;
 54               (*T)->bf=EH;
 55                L-bf=LH;
 56                break;
 57    }
 58    lR->bf=EH;
 59    L_Rotate(&(*T)->lchild);
 60    R_Rotate(T);
 61    }
 62 
 63 }  
 64 int InsertAVL(BITree *T,int n,int *taller)//taller用于判断插入节点后，树长高了没有
 65 {
 66  if(!*T)
 67    {
 68        *T=(BiTree)malloc(sizeod(BITNode));
 69        (*T)->data=e;
 70        (*T)->lchild=(*T)->rchild=NULL;
 71        (*T)->bf=EH;
 72         *taller=TRUE;
 73    }
 74  else{
 75        if(e==(*T)->data)
 76        {
 77        *taller=FALSE;
 78        return FALSE;
 79        }
 80        if(e<(*T)->data)
 81        {
 82         if(!InsertAVL(&(*T))->lchild,e,taller)
 83         {
 84            return FALSE;
 85          }
 86          if(*taller)//判断树的长势
 87          {
 88             switch((*T)->bf)
 89             {
 90               case LH:
 91                         LeftBalance(T);
 92                          *taller=FALSE;
 93                          break;
 94                case EH:
 95                            (*T)->bf=EH;
 96                            *taller=TRUE;
 97                            break;
 98                 case RH:
 99                           (*T)->bf=EH;
100                            *taller=FALSE;
101   
102             }  
103          }
104  
105         }
106         else
107         {
108           if(!InsertAVL(&(*T))->rchild,e,taller)
109           {
110            return FALSE;
111            }
112            if(*taller)//判断树的长势
113            {
114             switch((*T)->bf)
115             {
116               case LH:
117                         (*T)->bf=EH;
118                          *taller=FALSE;
119                          break;
120                case EH:
121                            (*T)->bf=EH;
122                            *taller=TRUE;
123                            break;
124                 case RH:
125                            RightBalance(T);
126                           (*T)->bf=EH;
127                            *taller=FALSE;
128   
129             }  
130          }
131  
132         }
133     }    
134 }

posted on 2015-06-21 21:49 星梦缘vs惜阅读(16008) 评论(1) 编辑收藏举报

刷新页面返回顶部