什么是图?
1:定义
图是由一个顶点集V和一个弧集R构成的数据结构。
Graph=(V,R),R={VR},VR={<v,w>| v,w∈V 且 P(v,w)}<v,w>表示从v到w的一条弧,并称v为弧尾,w为弧头。所谓词P(v,w)定义了弧 <v,w>的意义或信息。
2:术语
1)有向图、无向图、有向网、无向网、子图、子网
2)完全图、有向完全图、稀疏图、稠密图
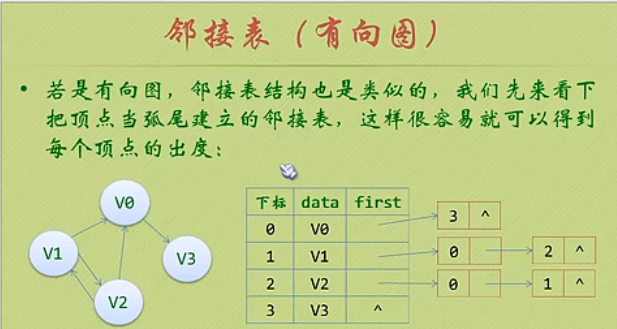
3)邻接点、度、入度、出度
4)路径、路径长度、回路、简单路径、简单回路
5)连通图、连通分量、强连通图、强连通分量
6)生成树、生成森林
由于“弧”是有方向的,因此称由顶点集和弧集构成的图为有向图。

假设图中有 n 个顶点,e 条边,则:含有e=n(n-1)/2 条边的无向图称作完全图;含有e=n(n-1) 条弧的有向图称作有向完全图;
若边或弧的个数e<nlogn,则称作稀疏图; 否则称作稠密图。





对于这里的第二条,-它含有图中全部的N个顶点,但是只有足以构成一棵树的N-1条边,上述图中一共有8个顶点,但是却有9条边,所以不是生成树,故需要去掉2条边,
 如图,就满足条件。
如图,就满足条件。
但是并不是所有的连通图去掉任意一条边就是极小联通子图,反例如下:
下面的也满足条件,但是却不能构成生成树。因为这些点不能完全连起来。


关于图的存储结构:


对角线上的元素:代表自己指向自己,由于这了没有路径用于这些指向,所以用0来代替。可见对角线的右上角的左下角是对称的,又为对称矩阵。对于对称矩阵,这里不再进行赘余。




对于十字链表,蓝色线表示的是:邻接表。红色线表示的是:逆邻接表。

这世界上有一种鸟是没有脚的,它只能够一直的飞呀飞呀,飞累了就在风里面睡觉,这种鸟一辈子只能下地一次,那一次就是它死亡的时候。



