python(5):scipy之numpy介绍
python 的scipy 下面的三大库: numpy, matplotlib, pandas
scipy 下面还有linalg 等
scipy 中的数据结构主要有三种: ndarray(n维数组), Series(变长字典), Dataframe(数据框)
numpy有强大的ndarray对象和ufunc(universal function 通用函数), 适合线性代数, 随机数处理等科学计算
Pandas 具有高效的 Series(变长字典), Dataframe(数据框) 数据结构
下面学习numpy
list ,tuple 也可以表示数组
一维: [1,2,3]; 二维数组: [[1,2,], [3,4]]
由于列表的元素可以是任何类型, 因此列表保存的是对象的指针, 比如[1,2,3,4] 需要四个指针与四个数值, 比较浪费内存和计算时间. ndarray是numpy的基本数据结构, 所有元素是同一种类型, 有丰富的函数, 计算效率也很高.

1. 示例
import numpy as np a=np.array([1,2,3]) # 生成一个数组 print(a) b=np.array([[1,2],[3,4]]) # 二维数组, 也可以b=np.array([(1,2),(3,4)]) print(b) print(np.arange(1,5,0.5)) #开始,结束,步长, 5取不到! #[ 1. 1.5 2. 2.5 3. 3.5 4. 4.5] # numpy 包里面也有random 函数 print(np.random.random((2,2)))#2*2随机浮点数数组 print(np.linspace(1,2,11,endpoint=False)) # 1-2之间插入数字, 共11个数 print(np.linspace(1,2,11)) #默认2能够取到, 即endpoint=True # [1. 1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 1.9 2. ] print(np.ones([2,3])) print(np.zeros([2,2])) # 这个功能超级强大 print(np.fromfunction(lambda i,j:(i+1)*(j+1),[2,3])) # 2*3数组
[1 2 3]
[[1 2]
[3 4]]
[1. 1.5 2. 2.5 3. 3.5 4. 4.5]
[[0.93912717 0.52333486]
[0.21249562 0.04995071]]
[1. 1.09090909 1.18181818 1.27272727 1.36363636 1.45454545
1.54545455 1.63636364 1.72727273 1.81818182 1.90909091]
[1. 1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 1.9 2. ]
[[1. 1. 1.]
[1. 1. 1.]]
[[0. 0.]
[0. 0.]]
[[1. 2. 3.]
[2. 4. 6.]]
数组的元素提取
import numpy as np a=np.array([(1,2,3),(4,5,6)]) print(a[1]) # [4 5 6] print(a[0:2]) #[[1 2 3] # [4 5 6]] print(a[:,[0,1]]) #[[1 2] # [4 5]] print(a[1,[0,1]]) # [4 5] for i in a: print(i) #[1 2 3] #[4 5 6]
数组的shape改变
import numpy as np a=np.array([(1,2,3),(4,5,6)]) print(a.shape) # (2, 3) b=a.reshape(3,2) # 没有改变a print(b) #[[1 2] # [3 4] # [5 6]] a.resize(3,2) # 改变了a
数组之间的拼接
import numpy as np a=np.array([1,2,3]) b=np.array([[1,2],[3,4]]) c=np.array([4,5,6]) print(np.hstack((a,c))) #横向连接 [1 2 3 4 5 6] print(np.vstack((a,c)))#纵向连接 得到2*3数组 print(b.T) #转置 print(a+c)#对应元素相加 [5 7 9]
结果:
[1 2 3 4 5 6];
[[1 2 3]
[4 5 6]] ;
[[1 3]
[2 4]] ;
[5 7 9];
不同形式的数组可以相加 相乘(对应元素之间)
import numpy as np a=np.array([1,2,3]) # 行向量 b=np.array([[1,3,5],[3,6,1]]) print(a+b) #[[2 5 8] #[4 8 4]] a=np.array([[1],[3]]) # 列向量 , 形状不同也可以相加, 但是一个维度要相等 b=np.array([[1,3,5],[3,6,1]]) print(a+b) #[[2 4 6] #[6 9 4]] # 但这里不可以是a=np.array([1,2]), a必须与b 的其中一个维度相等!!
通过list生成数组
import numpy as np a=np.array([1,2,3]) x=[1,2,3] xx=np.array(x) print(xx) # [1 2 3] y=[[1,2],[3,4]] yy=np.array(y) # 二维数组 print(yy) print(yy.flatten()) #展平,这不能作用于列表,只能作用于数组 [1 2 3 4]
对数组的简单运算
import numpy as np b=np.array([[1,2],[3,4]]) print(b.sum()) #10 print(b.sum(axis=0))#按列求和 [4 6] print(b.sum(axis=1))#按行求和 [3 7] print(b.min()) # 1 print(b.argmax())#max的下标 3 , 实际顺序按照列来排 print(b.mean()) # 2.5 print(b.std()) # 1.118
总结
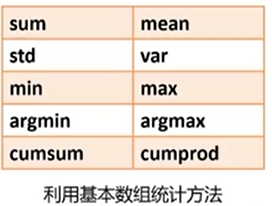
注意:数组的属性函数不需要末尾加() !!
b=np.array([[1,2],[3,4]]) print(b.size)#元素个数 4 print(b.ndim)#秩 2 print(b.shape) # (2L, 2L) print(b.dtype)#元素类型 int32
示例: numpy比math的计算速度更快
import numpy as np import time import math x=np.arange(0,100,0.01) t1=time.clock() for i,t in enumerate(x): x[i]=math.pow((math.sin(t)),2) t2=time.clock() y=np.arange(0,100,0.01) t3=time.clock() y=np.power(np.sin(y),2) t4=time.clock() print('running time of math is:',t2-t1) print('running time of numpy is:',t4-t3) ans: ('running time of math is:', 0.011655904997766612) ('running time of numpy is:', 0.0023625201675097404)
numpy与scipy的结合使用
(1)实现矩阵的一些运算
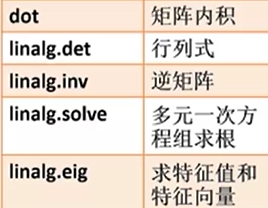
实例
import numpy as np from scipy import linalg a=np.array([[1,0],[1,2]]) print(np.dot(a,a)) # 矩阵乘法 print(linalg.det(a)) # 行列式=2.0 print(linalg.inv(a)) x,y=linalg.eig(a) print(x) #特征值 print(y)#特征向量??奇怪的值,随便给出的一个特征向量
结果:
[[1 0]
[3 4]]
2.0
[[ 1. -0. ]
[-0.5 0.5]]
[ 2.+0.j 1.+0.j]
[[ 0. 0.70710678]
[ 1. -0.70710678]]
实际上 , 不用import linalg也可以, numpy下面也有一个linalg
import numpy as np x=np.array([[1,2],[3,4]]) r1=np.linalg.det(x) print(r1) r2=np.linalg.inv(x) print(r2)
(2)聚类分析
import numpy as np from scipy.cluster.vq import vq,kmeans,whiten list1=[89,90,76,90] list2=[96,78,89,79] list3=[90,98,89,80] list4=[80,72,79,84] list5=[92,81,89,87] data=np.array([list1,list2,list3,list4,list5]) print(data) whiten=whiten(data) centroids,_=kmeans(whiten,2) result,_=vq(whiten,centroids) print(result)
[[89 90 76 90]
[96 78 89 79]
[90 98 89 80]
[80 72 79 84]
[92 81 89 87]] ;
[1 1 1 0 1] ;
三维数组
import numpy as np b=np.arange(24).reshape(2,3,4) print(b) print(b[1])#访问第二层 print(b[0,1,::2])#,[4 6]间隔是2 print(b[0,1,[1,2]]) # [5 6] print(b[::-1]) #两层交换 print(b.ravel())#展平变一维的数组 print(b.reshape(6,4))
结果:
[[[ 0 1 2 3]
[ 4 5 6 7]
[ 8 9 10 11]]
[[12 13 14 15]
[16 17 18 19]
[20 21 22 23]]]
[[12 13 14 15]
[16 17 18 19]
[20 21 22 23]]
[4 6]
[5 6]
[[[12 13 14 15]
[16 17 18 19]
[20 21 22 23]]
[[ 0 1 2 3]
[ 4 5 6 7]
[ 8 9 10 11]]]
[ 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23]
[[ 0 1 2 3]
[ 4 5 6 7]
[ 8 9 10 11]
[12 13 14 15]
[16 17 18 19]
[20 21 22 23]]
三维数组的一些操作
import numpy as np x=np.array([[1,2,3],[4,5,6],[7,8,9]]) #分割数组 x1,x2,x3=np.hsplit(x,3) print(x1) #得到[1,4,7] 列向量形式 y1,y2,y3=np.vsplit(x,3) print(y1)#得到[1,2,3] 行向量 z=np.array([1+2.j,3+4.j]) print(z.real) # [ 1. 3.] print(z.tolist()) # [(1+2j), (3+4j)] print(x.tolist())
[1]
[4]
[7]]
[[1 2 3]]
[ 1. 3.]
[(1+2j), (3+4j)]
[[1, 2, 3], [4, 5, 6], [7, 8, 9]]
numpy包中其他常用的函数
import numpy as np x=np.eye(2) print(x) np.savetxt('eye.txt',x) # 将结果保存到txt x1=np.array([9,30,20,39,12]) print(np.diff(x1)) # [ 21 -10 19 -27], 数组长度-1 print(np.ptp(x1)) # 30 极差: 最大最小的之差 print(np.median(x1)) # 20 print(np.msort(x1)) # [ 9 12 20 30 39]
[[ 1. 0.]
[ 0. 1.]], 得到txt文件如下

下标对应
import numpy as np d=np.array([1,2,4,11,27,34,2,21]) price=np.array([11,22,41,15,29,32,20,61]) ind=np.where(d==2) print(list(ind)) # [array([1, 6], dtype=int64)] print(np.take(price,ind)) # [[22 20]]
数组修剪
import numpy as np a=np.arange(6) print(a) # [0 1 2 3 4 5] a1=a.clip(2,3) # 比2 小的变2 ,变3 大的变3 print(a1) # a 没有改变! a1= [2 2 2 3 3 3] b=np.arange(6) print(b.compress(b>2)) #b没有改变! [3 4 5]
数组的连乘
import numpy as np a=np.arange(1,5) print(a.prod()) # 24 print(a.cumprod()) # [ 1 2 6 24]
统计: 协方差cov , 相关系数corr
import numpy as np a=np.array([1,4,9,-1,3,6]) b=np.array([11,24,19,-12,30,48]) cov=np.cov(a,b) # 生成协方差矩阵 print(cov) corr=np.corrcoef(a,b) print(corr) print(cov.diagonal()) #协方差矩阵的对角线 即为方差 [ 12.66666667 401.2 ] print(corr.trace()) # 相关系数矩阵你的对角线元素之和, 全为1,和一定=2.0
得到两个矩阵为:
[[ 12.66666667 45.6 ]
[ 45.6 401.2 ]]
[[ 1. 0.63966591]
[ 0.63966591 1. ]]
多项式拟合
import numpy as np a=np.array([1,4,9,3,6,12,19]) t=np.arange(len(a)) print(t) # [0 1 2 3 4 5 6] poly=np.polyfit(t,a,3) print(poly) #三次方差的系数,阶数由高到低:
# [ 0.36111111 -2.73809524 6.54365079 0.92857143] print(np.polyval(poly,0)) # 0.928571428571 print(np.polyval(poly,t[-1]+1)) # 预测下一个t 36.4285714286
np 数组转为list, 并排序等
import numpy as np a=np.array([1,4,9,3,6,12,19]) print(a.tolist()) # 列表 [1, 4, 9, 3, 6, 12, 19] print(np.argsort(a)) # 返回排序后的下标 [0 3 1 4 2 5 6] b=np.array([[10,8,3],[4,6,8]]) print(np.sort(b)) # 每行进行从小到大排布 print(np.msort(b)) # 每列进行从小到大排布
[[ 3 8 10]
[ 4 6 8]] ;
[[ 4 6 3]
[10 8 8]] ;
条件筛选
import numpy as np a=np.array([1,4,9,3,6,3,12,19]) print(np.where(a==3)) # (array([3, 5], dtype=int64),) print(np.extract(a>3,a)) # [ 4 9 6 12 19] 保留>3的数 print(np.take(a,[2,4])) # 找出a的下标是[2,4]的元素 为[9 6]
mod 余数问题
import numpy as np print(np.mod(10,-3))# -2 与除数的符号一致 print(np.mod(-10,3)) # 2 print(np.fmod(10,-3)) # 1 与被除数的符号一致 print(np.fmod(-10,-3)) # -1
print(x1*x2) # 两者等价 print(np.multiply(x1,x2))
条件
import numpy as np x=np.arange(10) print(np.where(x<5,9-x,x)) # [9 8 7 6 5 5 6 7 8 9] print(np.select([x<2,x>6,True],[7-x,x,2*x])) #[ 7 6 4 6 8 10 12 7 8 9] print(np.piecewise(x, [x<2,x>6], [lambda x:7-x,lambda x:x,lambda x:2*x])) a=np.array([1,4,2]) print(np.piecewise(a,[a==1],[100])) # [100 0 0] c=np.array([-2,4,10]) print(np.piecewise(c, [c>0, c<0], [-1,1])) # [-1,1,1]
Note: piecewise中funclist如果不是数值而是函数时要使用lambda表达式,不能使用简单表达式7-x,否则会出错
np库中的random函数
import numpy as np print(np.random.rand()) # print(np.random.rand(2,3)) print(np.random.standard_normal(2)) print(np.random.randint(2,6,(2,3))) # 2*3数组
0.10520553884752792
[[ 0.23205959 0.86906066 0.82928021]
[ 0.9032334 0.88635683 0.32403535]]
[-0.23941662 0.53619398]
[[5 4 4]
[2 3 3]]
综合应用实例
已知一只股票每日的收盘价信息:price.txt文件,第一个为space
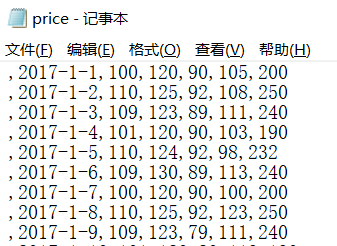
下面对收盘价c 成交量v等信息作简单统计
import numpy as np c,v=np.loadtxt(r'C:\Users\xuyin\Desktop\test\price.txt',\ delimiter=',',usecols=(5,6),unpack=True)#读取closedprice,与volume成交量 t=np.arange(len(c)) #计算VWAP(volume_weighted average price) vwap=np.average(c,weights=v) print vwap twap=np.average(c,weights=t)#(time_weighted average price) print twap print np.ptp(c)#极差 print c.ptp()#与上述一样 print np.median(c) print np.msort(c)#从小到大排列, print np.var(c) print c.var()#与上述一样
ans:
110.374338624
111.763157895
27.0
27.0
111.0
[ 98. 98. 100. 100. 103. 103. 103. 105. 108. 111. 111. 113.
113. 113. 115. 117. 119. 121. 123. 125.]
68.1475
68.1475
returns=np.diff(c)/c[:-1]#计算每日收益率(第一天没有) print returns good=np.where(returns>0)#获得index print good print len(good)#得到1,所以不能这么统计, print len(c[good]) print float(len(c[good])/float(len(c)-1)) print 'the number of profiting days is %.1f'%float(len(c[good])/float(len(c)-1)) logreturns=np.diff(np.log(c))#对数收益率 #如何快速将列表的数格式化?
ans:
[ 0.02857143 0.02777778 -0.07207207 -0.04854369 0.15306122 -0.11504425
0.23 -0.09756098 0.01801802 -0.13274336 0.21428571 -0.01680672
-0.11965812 0. 0.11650485 -0.13043478 0.13 0.07079646
0.03305785]
(array([ 0, 1, 4, 6, 8, 10, 14, 16, 17, 18], dtype=int64),)
1
10
0.526315789474
the number of profiting days is 0.5
APPLE一周股价的整理,
import numpy as np
import datetime
def datestr2num(s):
return datetime.datetime.strptime(s,'%Y-%m-%d').date().weekday()
#strptime(s,'%Y-%m-%d')表示将s转化为%Y-%m-%d'形式,date().weekday()表示一种格式,
#将周一_周日分别用0,1,2..6表示,注意y一定要大写Y!!!Y是四位数的年表示
o,h,l,c=np.loadtxt(r'C:\Users\xuyin\Desktop\test\price.txt',\
delimiter=',',usecols=(range(3,7)),unpack=True)
d=np.loadtxt(r'C:\Users\xuyin\Desktop\test\price.txt',\
delimiter=',',usecols=(1,),converters={1:datestr2num},unpack=True)
#计算工作日的收盘均值,剔除周末(5,6)
aveg=np.zeros(5)
for i in range(5):
ind=np.where(d==i)
aveg[i]=round(np.mean(c[ind]),2)
print aveg
#一周数据汇总,(源数据有三周的数据),要得到这三周的周open.high,low,close
#先找三周的数据剔除工作日的数据
#找到第一个周一,0与第三个周五
mon1=np.ravel(np.where(d==0))[0]#返回指标
fri3=np.ravel(np.where(d==4))[-1]
ind=np.arange(mon1,fri3+1)
weekind=[]#list
#剔除中间的2组5 6数据
for i in range(len(ind)):
if (i+1)%7!=6 and (i+1)%7!=0:
# print(i)
# print(ind[i])
weekind.append(ind[i])
weekind=np.array(weekind)
weekind=np.split(weekind,3)#分成三组
print weekind
def summarize(a,o,h,l,c):
weekopen=o[a[0]]#a表示指标
weekhigh=np.max(h[a])
weeklow=np.min(l[a])
weekclose=c[a[-1]]
return('APPLE',weekopen,weekhigh,weeklow,weekclose)
weeksummary=np.apply_along_axis(summarize,1,weekind,o,h,l,c)
#np.apply_along_axis会调用另一个函数作用于数组的每一个元素上
#numpy.apply_along_axis(func, axis, arr, *args, **kwargs):
#axis表示作用的轴,1表示横轴,
np.savetxt(r'C:\Users\xuyin\Desktop\weeksum.txt',\
weeksummary,delimiter=',',fmt='%s')#存储格式是s
weekp1=np.loadtxt(r'C:\Users\xuyin\Desktop\weeksum.txt',\
delimiter=',',usecols=(1,),unpack=True)#\表示续行
print weekp1
ans:
[ 243.33 210. 224. 237.33 240. ]
[array([1, 2, 3, 4, 5], dtype=int64), array([ 8, 9, 10, 11, 12], dtype=int64), array([15, 16, 17, 18, 19], dtype=int64)]
[ 125. 123. 130.]
#np.apply_along_axis会调用另一个函数作用于数组的每一个元素上
#numpy.apply_along_axis(func, axis, arr, *args, **kwargs):
#axis表示作用的轴,1表示横轴,
def my_func(a):
return (a[0] + a[-1]) * 0.5
b=np.array([[1,2,3,4],[5,6,7,8],[9,10,11,12]])
print np.apply_along_axis(my_func, 0, b)
#输出: array([ 5., 6., 7., 8.])
print np.apply_along_axis(my_func, 1, b)
#输出: array([ 2.5, 6.5, 10.5])
分析时间数据:???waiting ...太懒了还么, 未完待续
numpy as np
a=np.array([1,4,9,-1,3,6])
b=np.array([11,24,19,-12,30,48])
cov=np.cov(a,b) # 生成协方差矩阵
print(cov)
corr=np.corrcoef(a,b)
print(corr)
print(cov.diagonal()) #协方差矩阵的对角线 即为方差 [ 12.66666667 401.2 ]
print(corr.trace()) # 相关系数矩阵你的对角线元素之和, 全为1,和一定=2.0
import numpy as npa=np.array([1,2,3]) # 生成一个数组print(a)b=np.array([[1,2],[3,4]]) # 二维数组, 也可以b=np.array([(1,2),(3,4)]) print(b)print(np.arange(1,5,0.5)) #开始,结束,步长, 5取不到!#[ 1. 1.5 2. 2.5 3. 3.5 4. 4.5]# numpy 包里面也有random 函数print(np.random.random((2,2)))#2*2随机浮点数数组print(np.linspace(1,2,11,endpoint=False)) # 1-2之间插入数字, 共11个数print(np.linspace(1,2,11)) #默认2能够取到, 即endpoint=True# [1. 1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 1.9 2. ]print(np.ones([2,3]))print(np.zeros([2,2]))# 这个功能超级强大print(np.fromfunction(lambda i,j:(i+1)*(j+1),[2,3])) # 2*3数组




