常用算法之----旅行商问题

　　旅行商问题是np问题，在集合表示那里用set去实现效率很很低，而且要保存的数都是不重复的比较小的整数，所以这里用二进制串表示集合。比如集合{1,3,5,6,7}表示成二进制串用1110101，其中集合里面有的数对应的位数写成1，没有的写成0。要判断第3位是不是1，就把 1110101右移(3-1)位，得到11101，然后结果和00001进行 & 运算，如果结果是1说明第3位是1，否则说明第3位是0。

　　推广一下，对于数字x，要看它的第i位是不是1，那么可以通过判断布尔表达式 (((x >> (i - 1) ) & 1) == 1的真值来实现。

　　对于下面这个测试用例，图和邻接矩阵如下，不能走的话用-1表示，实际存储的时候用一个比较大的数字，比如0x7ffff：

 

 

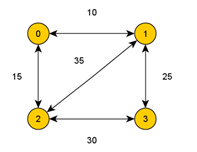
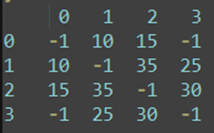
　　要使用动态规划，需要问题本身有最优子结构，我们需要找到要解决的问题的子问题。

　　题目要求，从0出发，经过[1,2,3]这几个城市，然后回到0，使得花费最少。要实现这个要求，需要从下面三个实现方案中选择花费最少的方案。

　　　　1、 从0出发，到1，然后再从1出发，经过[2,3]这几个城市，然后回到0，使得花费最少。

　　　　2、 从0出发，到2，然后再从2出发，经过[1,3]这几个城市，然后回到0，使得花费最少。

　　　　3、 从0出发，到3，然后再从3出发，经过[1,2]这几个城市，然后回到0，使得花费最少。

　　可以发现，三个小的解决方案的最优解，构成了大的解决方案，所以这个问题具有最优子结构，可以用动态规划来实现。

　　设置一个二维的动态规划表dp,定义符号{1,2,3}表示经过[1,2,3]这几个城市，然后回到0。

　　那么题目就是求dp[0][{1,2,3}]。将{1,2,3}表示成二进制，就是111，对应10进制的7，所以题目是在求dp[0][7];

　　要求三个方案的最小值意味：

　　　　dp[0][{1,2,3}] = min{ C01+dp[1][{2,3}] ，C02+dp[2][{1,3}] ，C03+dp[3][{1,2}]}

　　　　其中C01 表示从0出发到1的距离。

　　　　dp[1][{2,3}] = min{ C12+dp[2][{3}] ，C13+dp[3][{1}]}

　　　　dp[2][{3}] = C23+dp[3][{}]

　　　　dp[3][{}]就是从3出发，不经过任何城市，回到0的花费，所以dp[3][{}] = C30

 

　　先确定一下dp表的大小，有n个城市，从0开始编号，那么dp表的行数就是n，列数就是2^(n-1)，即1 << （n – 1）,集合{1,2,3}的子集个数。在求解的时候，第一列的值对应这从邻接矩阵可以导出，后面的列可以有前面的列和邻接矩阵导出。所以求出的动态规划表就是：

 

 

j = 0　　第一轮

for(int i =0;i <n;i++){                      
    dp[i][0] = C[i][0];                        
}

　　第二轮

j = 1;       //可以把j带入
for(int i = 0;i < n;i++){
    dp[i][j] = C[i][1]+dp[1][0]
}

　　后面的规律比较麻烦的一点在于要集合和二进制转换，观察发现：

　　　　dp[2][5] 表示从2出发，通过｛1，3｝，最后回到起点。那么:

　　　　dp[2][5] = min{C21 + dp[1][{3}],C23 + dp[3][{1}]} = min{C21 + dp[1][4],C23 + dp[3][1]} ;

　　　　从2出发，要去{1,3}。

　　　　先看去1的路，去了1集合{1,3}中只剩下{3} ,{3}对应4,所以要求的dp表就是dp[1][4],这个4可以通过(101) ^ (1)得到,(1) = 1<<(1-1)

　　　　再看去2的路，5 = 101的第二位是0，所以不能去2。判断第二位为1，用(5>>(2-1)) &1==1。而且也由于从2出发，就更不能去了。

　　　　最后看去3的路，去了3集合{1,3}中只剩下{1},{1}对应这1，所以要求的dp表就是dp[3][1],1通过(101) ^ (100)得到。(100) = 1<<(3-1)

 

　　　　同样求dp[0][7] = min{C01 + dp[1][6], C02+ dp[2][5], C03 + dp[3][3]}

　　　　从0出发，要去{1,2,3}

　　　　先看去1的路，去1然后去6 = {2,3},6通过(111) ^ (1)得到,(1) = 1<<(1-1)

　　　　再看去2的路，去2然后去5 = {1,3},5通过(111) ^ (10)得到。(10) = 1<<(2-1)

　　　　最后看去3的路，去3然后去3 = {1,2},3通过(111) ^ (100)得到。(100) = 1<<(3-1)

 

　　　　还要注意，求dp[2][3]的时候。就是求从2出发，经过{1,2}，显然不合理，在dp表中应为-1。对于这种情况，只用判断数字3的二进制位的第2位是不是1，是1就表示不合理。

 

　　根据以上的推导，最后求dp表的算法就是：

for(int j = 1;j < 1 << (n - 1);j++){        
    for(int  i= 0;i < n;i++){               
        dp[i][j] = 0x7ffff;
        if(((j >> (i - 1)) & 1) == 1){          
            continue;   
        }   
        for(int k = 1;k < n;k++){       
            if(((j >> (k - 1)) & 1) == 0){
                continue;                           
            }
            if(dp[i][j] > C[i][k] + dp[k][j ^ (1 << (k - 1))]){
                dp[i][j] = C[i][k] + dp[k][j ^ (1 << (k - 1))];
            }
        }
    }
}

　　最终程序的返回值就是dp表左上角的那个数字return dp[0][(1<<(cityCount - 1)) - 1];

　　一个完整运行的例子是：

public class TravelingSalesman {
    public static void main(String[] args) {
        int cityCount = 4;
        int[][] roadInfo = new int[][]{
             {0, 1, 10},
             {1, 0, 10},
             {1, 3, 25},
             {3, 1, 25},
             {3, 2, 30},
             {2, 3, 30},
             {0, 2, 15},
             {2, 0, 15},
             {1, 2, 35},
             {2, 1, 35}
        };
        
        int roadmap[][] = new int[cityCount][cityCount];        //转成邻接矩阵方便取数
        int dp[][] = new int [cityCount][1 << (cityCount - 1)];
        for(int i = 0;i < cityCount;i++){
            for(int j = 0;j < cityCount;j++){    
                roadmap[i][j] = 0x7ffff;                        //用0x7ffff表示无穷大
            }
        }
        for(int i = 0;i < roadInfo.length;i++){                 //邻接矩阵
            roadmap[roadInfo[i][0]][roadInfo[i][1]] = roadInfo[i][2];
        }

        for(int i =0;i <cityCount;i++){                          //先求dp表第一列
            dp[i][0] = roadmap[i][0];                            //求出了每个城市回到起点的距离了。
        }
                                                
        for(int j = 1;j < 1 << (cityCount - 1);j++){             //再求其他列
            for(int  i= 0;i < cityCount;i++){                    //从i出发，要去包含j = {010101}的    城市
                dp[i][j] = 0x7ffff;
                if(((j >> (i - 1)) & 1) == 1){                   //如果已经到过j了，就continue
                    continue;    
                }    
                for(int k = 1;k < cityCount;k++){                 //看能不能先到k城市
                    if(((j >> (k - 1)) & 1) == 0){
                        continue;                                 //不能先到k城市，continue;
                    }
                    if(dp[i][j] > roadmap[i][k] + dp[k][j ^ (1 << (k - 1))]){
                        dp[i][j] = roadmap[i][k] + dp[k][j ^ (1 << (k - 1))];
                    }
                }
            }
        }
        System.out.println(dp[0][(1<<(cityCount - 1)) - 1]);
    }
}

　　若要显示dp表，可以在求出dp表以后加上一下代码：

System.out.printf("%10d",0);
for(int j = 0;j < 1 << (cityCount - 1) ;j++){
    System.out.printf("%10d",j);
}
System.out.println();
for(int i = 0;i < cityCount;i++){
    System.out.printf("%10d",i);
    for(int j = 0;j < 1 << (cityCount - 1) ;j++){
        if(dp[i][j] == 0x7ffff) dp[i][j] = -1;
        System.out.printf("%10d",dp[i][j]);
    }
    System.out.println();
}

　　本文章纯原创，转载请注明出处：http://www.cnblogs.com/youmuchen/