常用算法之——广度优先搜索
广度优先搜索的概念
广度优先搜索(BFS)类似于二叉树的层序遍历算法,它的基本思想是:首先访问起始顶点v,然后由v出发,依次访问v的各个未被访问过的邻接顶点w1,w2,w3….wn,然后再依次访问w1,w2,…,wi的所有未被访问过的邻接顶点,再从这些访问过的顶点出发,再访问它们所有未被访问过的邻接顶点….以此类推,直到途中所有的顶点都被访问过为止。类似的想法还将应用与Dijkstra单源最短路径算法和Prim最小生成树算法。(这个过程我觉得可以举个这样的例子来理解:比如要从你开始介绍你的家人,可以先从你开始,然后一个一个介绍和你有直接血缘关系的这一层亲属(爸爸妈妈儿子女儿),当把你所有的这些第一层亲属全都遍历完之后再从你的妈妈开始遍历(也可以从爸爸或儿子),把你妈妈的有直接血缘关系的亲戚先遍历一遍,然后再从爸爸开始,以此类推,直到全部都遍历完成)。
广度优先搜索是一种分层的查找过程,每向前走一步可能访问一批顶点,不像深度优先搜索那样有回退的情况(另一篇博客会介绍),因此它不是一个递归的算法,为了实现逐层的访问,算法必须借助一个辅助队列并且以非递归的形式来实现。
算法伪代码
其伪代码如下:
bool visited[MAX_VERTEX_NUM];//访问数组,也就是顶点个数
void BFSTraverse(Graph G)
//外层的函数,为准备实现遍历做一些准备工作。
{
for(int i=0;i<G.vexnum;++i)
visited[i]=false;//先将所有的顶点都设置为没有被访问过
InitQueue(Q);//初始化辅助队列方便遍历顶点
for(int i=0;i<G.vexnum;++i)
if(!visited[i])
BFS(G,i);
//外层循环使用if语句来调用BFS的原因是为了防止有的顶点它不能从初始顶点出发而遍历到,所以这里需要一个完全的循环来避免这种极端情况。
}
void BFS(Graph G,int v)
//从顶点v出发,广度优先遍历图G,算法借助了一个辅助队列Q
visit(v);//visit函数访问这个顶点的信息
visited[v]=true;//访问过了这个顶点之后就将这个顶点设置为已访问,即true
Enqueue(Q,v);//将顶点v入队列,这样就可以从队列中出队并访问它的相邻顶点
while(!isEmpty(Q)){
DeQueue(Q,v);//将队头的元素出队列存储在v
for(w=FirstNeighbor(G,v);w>=0;w=NextNeighbor(G,v,w))//这一步是检查v的所有邻接顶点
if(!visited[w]){
visit(w);
visited[w]=true;
EnQueue(Q,w);
//如果w没有被访问过,那么访问这个顶点,并把它入队
}
}实例以及解析
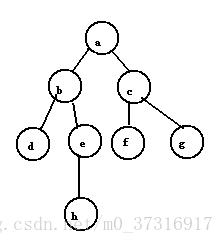
假设从a顶点开始访问,a先入队。此时队列非空,取出队头元素a,由于b,c和a直接相邻且未被访问过,于是依次访问b,c,并且b,c依次入队。队列非空,取出队头元素b,依次访问与b相邻且未被访问的顶点d,e,并且将d,e入队(注意:a与b也邻接,但是a已经访问过,就不会再访问了)。此时队列非空,取出队头元素c,访问与c邻接且未被访问过的顶点f,g,并且将f,g入队。此时,取出队头元素d,但与d邻接且为被访问的顶点为空,故不再进行任何操作,继续取出对头元素e,将h入队….当最后取出队头元素h后,队列为空,从而循环自动跳出,遍历的结果为abcdefgh。
BFS算法性能分析
无论是邻接表还是邻接矩阵的存储访问,BFS算法都需要借助一个辅助队列Q,n个顶点都需要入队依次,在最坏的情况下,空间复杂度为O(|V|)。
当采用邻接表存储方式时,每个顶点均需要搜索依次(或入队依次),故时间复杂度为O(|V|),再搜索任一顶点时,每条边至少访问依次,故时间复杂度为O(|E|),算法的总时间复杂度为O(|V|+|E|);当采用邻接矩阵存储方式的时候,查找每个顶点的邻接点所需时间为O(|V|),故算法总的时间复杂度为O(|V|²)。
BFS算法求单源最短路径问题
如果图G=(V,E)为非带权图。定义从顶点u到顶点v的最短路径d(u,v)为从u到v的任何路径中最少的边数;如果从u到v没有通路,则d(u,v)=∞。
使用BFS,我们可以求解一个满足上述定义的非带权图的单源最短路径问题,这是由广度优先搜索总是按照距离由近到远来遍历图中每个顶点的性质决定的(这让我想到:在2d游戏中计算两个位置的最短路径是否可以采用BFS算法来求出呢?)
BFS算法求解单源最短路径问题的算法如下:
void BFS_MIN_Distance(Graph G,int u){
//d[i]表示从u到i结点的最短路径
for(i=0;i<G.vexnum;++i)
d[i]=∞; //初始化路径长度
visited[u]=true;
d[u]=0;
while(!isEmpty(Q)){
DeQueue(Q,u);
for(w=FirstNeighbor(G,u);w>=0;w=NextNeighbor(G,u,w))
if(!visited[w]){//w为u未曾访问的邻接顶点
visited[w]=true;//设为已经访问
d[w]=d[u]+1;//路径长度+1
EnQueque(Q,w);//w顶点入队
}
}
}


