常用算法之----快速排序
快速排序由C. A. R. Hoare在1962年提出。它的基本思想是:通过一趟排序将要排序的数据分割成独立的两部分,其中一部分的所有数据都比另外一部分的所有数据都要小,然后再按此方法对这两部分数据分别进行快速排序,整个排序过程可以递归进行,以此达到整个数据变成有序序列
基本步骤
总的说来,要直接默写出快速排序还是有一定难度的,因为本人就自己的理解对快速排序作了下白话解释,希望对大家理解有帮助,达到快速排序,快速搞定。
快速排序是C.R.A.Hoare于1962年提出的一种划分交换排序。它采用了一种分治的策略,通常称其为分治法(Divide-and-ConquerMethod)。
该方法的基本思想是:
1.先从数列中取出一个数作为基准数。
2.分区过程,将比这个数大的数全放到它的右边,小于或等于它的数全放到它的左边。
3.再对左右区间重复第二步,直到各区间只有一个数。
虽然快速排序称为分治法,但分治法这三个字显然无法很好的概括快速排序的全部步骤。因此我的对快速排序作了进一步的说明:挖坑填数+分治法:
先来看实例吧,定义下面再给出(最好能用自己的话来总结定义,这样对实现代码会有帮助)。
以一个数组作为示例,取区间第一个数为基准数。
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
72 |
6 |
57 |
88 |
60 |
42 |
83 |
73 |
48 |
85 |
初始时,i = 0; j = 9; X = a[i] = 72
由于已经将a[0]中的数保存到X中,可以理解成在数组a[0]上挖了个坑,可以将其它数据填充到这来。
从j开始向前找一个比X小或等于X的数。当j=8,符合条件,将a[8]挖出再填到上一个坑a[0]中。a[0]=a[8]; i++; 这样一个坑a[0]就被搞定了,但又形成了一个新坑a[8],这怎么办了?简单,再找数字来填a[8]这个坑。这次从i开始向后找一个大于X的数,当i=3,符合条件,将a[3]挖出再填到上一个坑中a[8]=a[3]; j--;
数组变为:
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
48 |
6 |
57 |
88 |
60 |
42 |
83 |
73 |
88 |
85 |
i = 3; j = 7; X=72
再重复上面的步骤,先从后向前找,再从前向后找。
从j开始向前找,当j=5,符合条件,将a[5]挖出填到上一个坑中,a[3] = a[5]; i++;
从i开始向后找,当i=5时,由于i==j退出。
此时,i = j = 5,而a[5]刚好又是上次挖的坑,因此将X填入a[5]。
数组变为:
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
48 |
6 |
57 |
42 |
60 |
72 |
83 |
73 |
88 |
85 |
可以看出a[5]前面的数字都小于它,a[5]后面的数字都大于它。因此再对a[0…4]和a[6…9]这二个子区间重复上述步骤就可以了。
上述过程详细步骤:
0:72,6,57,88,60,42,83,73,48,85,x=72
1:48,6,57,88,60,42,83,73,__,85
2:48,6,57,__,66,42,83,73,88,85
3:48,6,57,42,66,__,83,73,88,85
3:48,6,57,42,66,__,83,73,88,85
4:48,6,57,42,66,72,83,73,88,85
经过这一轮排序后,基准数(72)左边的数都比72小,右边的都比它大,剩下的就是利用分治算法分别解决左右两边的数了。
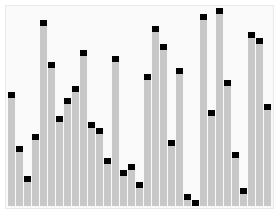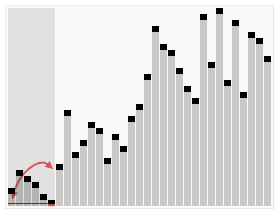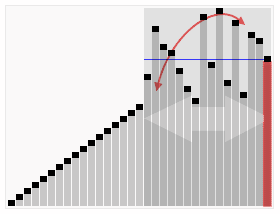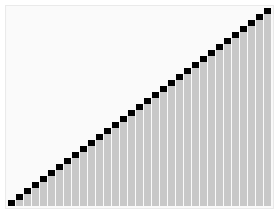
快速排序动画演示
对挖坑填数进行总结
1.i =L; j = R; 将基准数挖出形成第一个坑a[i]。
2.j--由后向前找比它小的数,找到后挖出此数填前一个坑a[i]中。
3.i++由前向后找比它大的数,找到后也挖出此数填到前一个坑a[j]中。
4.再重复执行2,3二步,直到i==j,将基准数填入a[i]中。
照着这个总结很容易实现挖坑填数的代码:
-
int AdjustArray(int s[], int l, int r) //返回调整后基准数的位置
-
{
-
int i = l, j = r;
-
int x = s[l]; //s[l]即s[i]就是第一个坑
-
while (i < j)
-
{
-
// 从右向左找小于x的数来填s[i]
-
while(i < j && s[j] >= x)
-
j--;
-
if(i < j)
-
{
-
s[i] = s[j]; //将s[j]填到s[i]中,s[j]就形成了一个新的坑
-
i++;
-
}
-
-
// 从左向右找大于或等于x的数来填s[j]
-
while(i < j && s[i] < x)
-
i++;
-
if(i < j)
-
{
-
s[j] = s[i]; //将s[i]填到s[j]中,s[i]就形成了一个新的坑
-
j--;
-
}
-
}
-
//退出时,i等于j。将x填到这个坑中。
-
s[i] = x;
-
-
return i;
-
}
再写分治法的代码:
-
void quick_sort1(int s[], int l, int r)
-
{
-
if (l < r)
-
{
-
int i = AdjustArray(s, l, r);//先成挖坑填数法调整s[]
-
quick_sort1(s, l, i - 1); // 递归调用
-
quick_sort1(s, i + 1, r);
-
}
-
}
这样的代码显然不够简洁,对其组合整理下:
//快速排序快速排序还有很多改进版本,如随机选择基准数,区间内数据较少时直接用另的方法排序以减小递归深度。有兴趣的筒子可以再深入的研究下。
注1,有的书上是以中间的数作为基准数的,要实现这个方便非常方便,直接将中间的数和第一个数进行交换就可以了。
本文在此篇博客上做补充:
参考博客:
http://www.cnblogs.com/Braveliu/archive/2013/01/11/2857222.html
http://developer.51cto.com/art/201403/430986.htm
http://blog.csdn.net/wolinxuebin/article/details/7456330
http://www.cnblogs.com/surgewong/p/3381438.html
http://www.ruanyifeng.com/blog/2011/04/quicksort_in_javascript.html
三数取中
在快排的过程中,每一次我们要取一个元素作为枢纽值,以这个数字来将序列划分为两部分。在此我们采用三数取中法,也就是取左端、中间、右端三个数,然后进行排序,将中间数作为枢纽值。
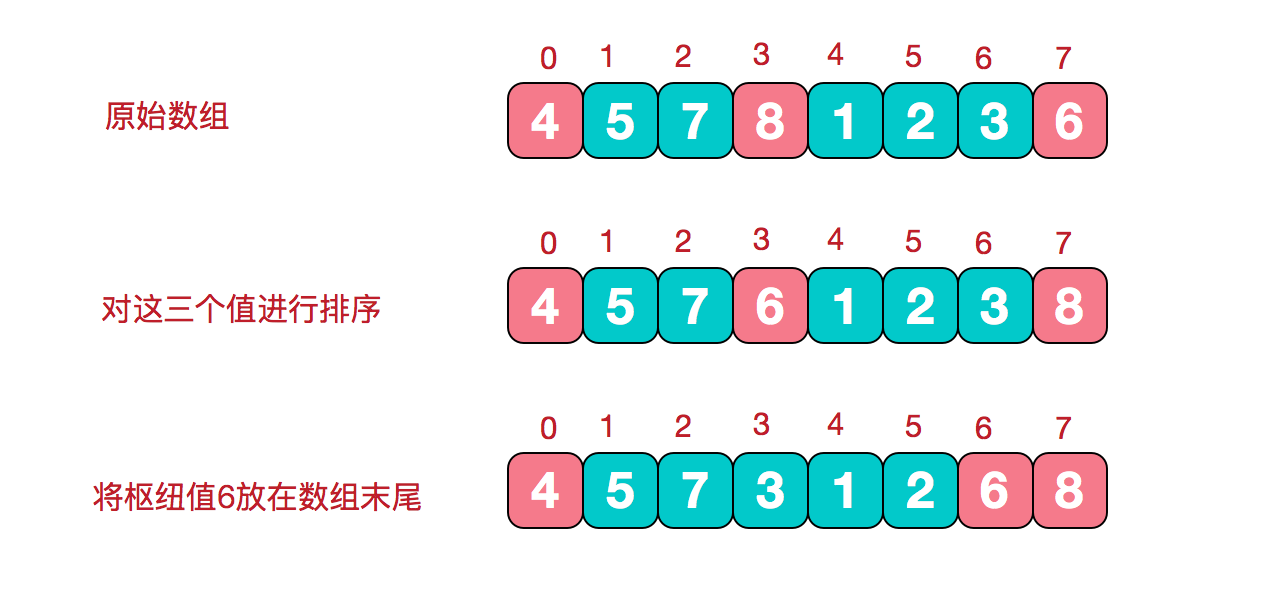
根据枢纽值进行分割
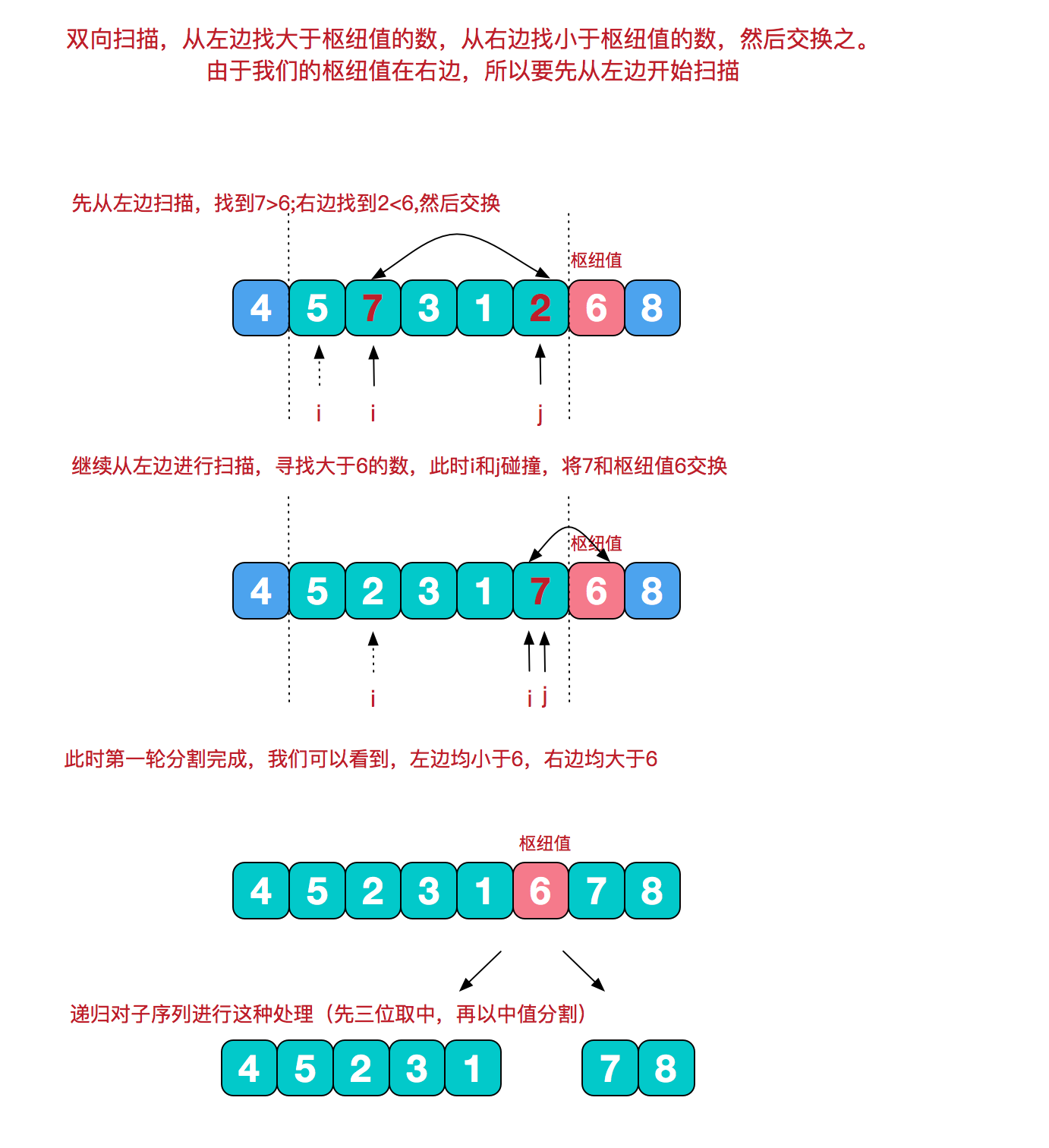

java代码实现
package sortdemo;
import java.util.Arrays;
/**
* Created by chengxiao on 2016/12/14.
* 快速排序
*/
public class QuickSort {
public static void main(String[] args) {
int[] arr = {9, 8, 7, 6, 5, 4, 3, 2, 1, 0};
quickSort(arr, 0, arr.length - 1);
System.out.println("排序结果:" + Arrays.toString(arr));
}
/**
* @param arr
* @param left 左指针
* @param right 右指针
*/
public static void quickSort(int[] arr, int left, int right) {
if (left < right) {
//获取枢纽值,并将其放在当前待处理序列末尾
dealPivot(arr, left, right);
//枢纽值被放在序列末尾
int pivot = right - 1;
//左指针
int i = left;
//右指针
int j = right - 1;
while (true) {
while (arr[++i] < arr[pivot]) {
}
while (j > left && arr[--j] > arr[pivot]) {
}
if (i < j) {
swap(arr, i, j);
} else {
break;
}
}
if (i < right) {
swap(arr, i, right - 1);
}
quickSort(arr, left, i - 1);
quickSort(arr, i + 1, right);
}
}
/**
* 处理枢纽值
*
* @param arr
* @param left
* @param right
*/
public static void dealPivot(int[] arr, int left, int right) {
int mid = (left + right) / 2;
if (arr[left] > arr[mid]) {
swap(arr, left, mid);
}
if (arr[left] > arr[right]) {
swap(arr, left, right);
}
if (arr[right] < arr[mid]) {
swap(arr, right, mid);
}
swap(arr, right - 1, mid);
}
/**
* 交换元素通用处理
*
* @param arr
* @param a
* @param b
*/
private static void swap(int[] arr, int a, int b) {
int temp = arr[a];
arr[a] = arr[b];
arr[b] = temp;
}
}
c代码如下:以最后一个为基准
#include <stdio.h>
// 分类 ------------ 内部比较排序
// 数据结构 --------- 数组
// 最差时间复杂度 ---- 每次选取的基准都是最大(或最小)的元素,导致每次只划分出了一个分区,需要进行n-1次划分才能结束递归,时间复杂度为O(n^2)
// 最优时间复杂度 ---- 每次选取的基准都是中位数,这样每次都均匀的划分出两个分区,只需要logn次划分就能结束递归,时间复杂度为O(nlogn)
// 平均时间复杂度 ---- O(nlogn)
// 所需辅助空间 ------ 主要是递归造成的栈空间的使用(用来保存left和right等局部变量),取决于递归树的深度,一般为O(logn),最差为O(n)
// 稳定性 ---------- 不稳定
void Swap(int A[], int i, int j)
{
int temp = A[i];
A[i] = A[j];
A[j] = temp;
}
int Partition(int A[], int left, int right) // 划分函数
{
int pivot = A[right]; // 这里每次都选择最后一个元素作为基准
int tail = left - 1; // tail为小于基准的子数组最后一个元素的索引
for (int i = left; i < right; i++) // 遍历基准以外的其他元素
{
if (A[i] <= pivot) // 把小于等于基准的元素放到前一个子数组末尾
{
Swap(A, ++tail, i);
}
}
Swap(A, tail + 1, right); // 最后把基准放到前一个子数组的后边,剩下的子数组既是大于基准的子数组
// 该操作很有可能把后面元素的稳定性打乱,所以快速排序是不稳定的排序算法
return tail + 1; // 返回基准的索引
}
void QuickSort(int A[], int left, int right)
{
if (left >= right)
return;
int pivot_index = Partition(A, left, right); // 基准的索引
QuickSort(A, left, pivot_index - 1);
QuickSort(A, pivot_index + 1, right);
}
int main()
{
int A[] = { 5, 2, 9, 4, 7, 6, 1, 3, 8 }; // 从小到大快速排序
int n = sizeof(A) / sizeof(int);
QuickSort(A, 0, n - 1);
printf("快速排序结果:");
for (int i = 0; i < n; i++)
{
printf("%d ", A[i]);
}
printf("\n");
return 0;
}
排序结果
排序结果:[1, 2, 3, 4, 5, 6, 7, 8]
快速排序是不稳定的排序算法,不稳定发生在基准元素与A[tail+1]交换的时刻。
比如序列:{ 1, 3, 4, 2, 8, 9, 8, 7, 5 },基准元素是5,一次划分操作后5要和第一个8进行交换,从而改变了两个元素8的相对次序。
Java系统提供的Arrays.sort函数。对于基础类型,底层使用快速排序。对于非基础类型,底层使用归并排序。请问是为什么?
答:这是考虑到排序算法的稳定性。对于基础类型,相同值是无差别的,排序前后相同值的相对位置并不重要,所以选择更为高效的快速排序,尽管它是不稳定的排序算法;而对于非基础类型,排序前后相等实例的相对位置不宜改变,所以选择稳定的归并排序。
总结
快速排序是一种交换类的排序,它同样是分治法的经典体现。在一趟排序中将待排序的序列分割成两组,其中一部分记录的关键字均小于另一部分。然后分别对这两组继续进行排序,以使整个序列有序。在分割的过程中,枢纽值的选择至关重要,本文采取了三位取中法,可以很大程度上避免分组"一边倒"的情况。快速排序平均时间复杂度也为O(nlogn)级。