DFS/BFS模板
本题是让我们把二叉树的每一层节点放入到同一个列表中,最后返回各层的列表组成的总的列表。
可以使用 BFS 和 DFS 解决。
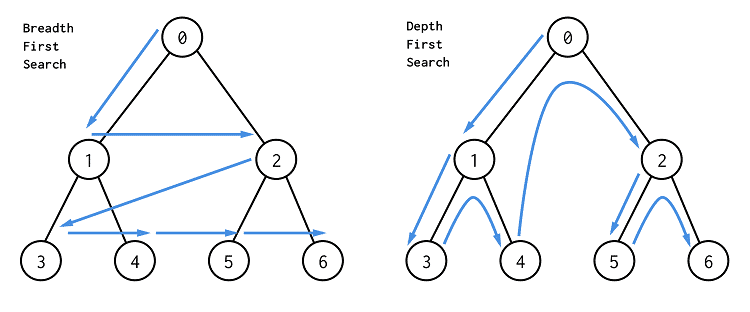
左边是BFS,按照层进行搜索;图右边是DFS,先一路走到底,然后再回头搜索。
BFS
BFS使用队列,把每个还没有搜索到的点依次放入队列,然后再弹出队列的头部元素当做当前遍历点。BFS总共有两个模板:
- 如果不需要确定当前遍历到了哪一层,BFS模板如下。
while queue 不空:
cur = queue.pop()
for 节点 in cur的所有相邻节点:
if 该节点有效且未访问过:
queue.push(该节点)
- 如果要确定当前遍历到了哪一层,BFS模板如下。
这里增加了level表示当前遍历到二叉树中的哪一层了,也可以理解为在一个图中,现在已经走了多少步了。size表示在当前遍历层有多少个元素,也就是队列中的元素数,我们把这些元素一次性遍历完,即把当前层的所有元素都向外走了一步。
level = 0
while queue 不空:
size = queue.size()
while (size --) {
cur = queue.pop()
for 节点 in cur的所有相邻节点:
if 该节点有效且未被访问过:
queue.push(该节点)
}
level ++;
上面两个是通用模板,在任何题目中都可以用,是要记住的!
本题要求二叉树的层次遍历,所以同一层的节点应该放在一起,故使用模板二。
使用队列保存每层的所有节点,每次把队列里的原先所有节点进行出队列操作,再把每个元素的非空左右子节点进入队列。因此即可得到每层的遍历。
各语言的代码如下:
# Definition for a binary tree node.
# class TreeNode(object):
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution(object):
def levelOrder(self, root):
"""
:type root: TreeNode
:rtype: List[List[int]]
"""
queue = collections.deque()
queue.append(root)
res = []
while queue:
size = len(queue)
level = []
for _ in range(size):
cur = queue.popleft()
if not cur:
continue
level.append(cur.val)
queue.append(cur.left)
queue.append(cur.right)
if level:
res.append(level)
return res
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
vector<vector<int>> levelOrder(TreeNode* root) {
queue<TreeNode*> que;
que.push(root);
vector<vector<int>> res;
while (que.size() != 0) {
int size = que.size();
vector<int> level;
while (size --) {
TreeNode* cur = que.front();
que.pop();
if (!cur) {
continue;
}
level.push_back(cur->val);
que.push(cur->left);
que.push(cur->right);
}
if (level.size() != 0) {
res.push_back(level);
}
}
return res;
}
};
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
public List<List<Integer>> levelOrder(TreeNode root) {
List<List<Integer>> res = new ArrayList<>();
Queue<TreeNode> q = new LinkedList<>();
q.offer(root);
while (!q.isEmpty()) {
int size = q.size();
List<Integer> level = new LinkedList<>();
for (int i = 0; i < size; ++i) {
TreeNode cur = q.peek();
q.poll();
if (cur == null) {
continue;
}
level.add(cur.val);
q.offer(cur.left);
q.offer(cur.right);
}
if (!level.isEmpty()) {
res.add(level);
}
}
return res;
}
}
DFS
本题使用 DFS 同样能做。由于题目要求每一层的节点都是从左到右遍历,因此递归时也要先递归左子树、再递归右子树。
DFS 做本题的主要问题是: DFS 不是按照层次遍历的。为了让递归的过程中同一层的节点放到同一个列表中,在递归时要记录每个节点的深度 level。递归到新节点要把该节点放入 level 对应列表的末尾。
当遍历到一个新的深度 level,而最终结果 res 中还没有创建 level 对应的列表时,应该在 res 中新建一个列表用来保存该 level 的所有节点。
各语言的代码如下:
# Definition for a binary tree node.
# class TreeNode(object):
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution(object):
def levelOrder(self, root):
"""
:type root: TreeNode
:rtype: List[List[int]]
"""
res = []
self.level(root, 0, res)
return res
def level(self, root, level, res):
if not root: return
if len(res) == level: res.append([])
res[level].append(root.val)
if root.left: self.level(root.left, level + 1, res)
if root.right: self.level(root.right, level + 1, res)
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
vector<vector<int>> levelOrder(TreeNode* root) {
vector<vector<int>> res;
dfs(res, root, 0);
return res;
}
void dfs(vector<vector<int>>& res, TreeNode* root, int level) {
if (!root) return;
if (level >= res.size())
res.push_back(vector<int>());
res[level].push_back(root->val);
dfs(res, root->left, level + 1);
dfs(res, root->right, level + 1);
}
};
class Solution {
public List<List<Integer>> levelOrder(TreeNode root) {
List<List<Integer>> res = new ArrayList<>();
if(root != null){
dfs(res, root, 0);
}
return res;
}
private void dfs(List<List<Integer>> res, TreeNode node, int level){
if(res.size() - 1 < level){
res.add(new ArrayList<Integer>());
}
res.get(level).add(node.val);
if(node.left!=null){
dfs(res, node.left, level + 1);
}
if(node.right!=null){
dfs(res, node.right, level + 1);
}
}
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号