快速排序
1.快速排序描述
1.每一轮排序选择一个基准点(pivot)进行分区
1.让小于基准点的元素进入一个分区,大于基准点的元素进入另一个分区
2.当分区完成时,基准点元素的位置就是其最终位置
2.在子分区重复以上过程,直至子分区元素个数少于等于1,这体现的是分而治之的思想(divide-and-conquer)
2.单边循环快排 (lomuto 洛穆托分区方案)
1.选择最右元素作为基准点元素
2. i 指针维护小于基准点元素的边界,也是每次交换的目标索引
3. j 指针负责找到比基准点小的元素,一旦找到则与 i 进行交换
4.最后基准点与i交换,i即为分区位置
3.特点
1.平均时间复杂度是 O(n㏒ⁿ) ,最坏时间复杂度是 O(n²)
2.数据量较大时,优势非常明显
3.属于不稳定排序
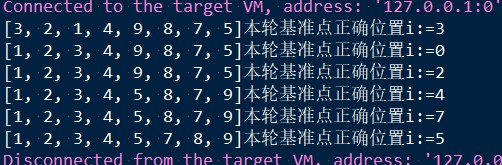
/** * 快速排序 (单边循环方法) */ public class QuickSort { public static void main(String[] args) { // 原始数据 int[] arr = {5,3,7,2,9,8,1,4}; quickSort(arr,0,arr.length - 1); } //快速排序方法 递归方法 public static void quickSort(int[] arr,int l,int h) { if (l >= h) { // 代表没有可以执行的分区退出递归 return; } //调用分区方法 获取每轮分组的边界 int p = partition(arr, l, h); //左边分区的范围确定 quickSort(arr,l,p - 1); //右边分区的范围确定 quickSort(arr,p + 1,h); } //分区方法 public static int partition(int[] arr ,int l,int h) { // pv是基准点元素,h 是分区上限也是本轮分区基准点 int pv = arr[h]; // i 是交换目标索引,l 是左边界 int i = l; // j 开始循环获取比基准点小的值 for (int j = l; j < h; j++) { if (arr[j] < pv) { if (i != j) { // 如果比较的元素小于基准点, // 并且他不是目标索引的位置, // 就把j元素交换到目标索引位置 swap(arr,i,j); } // 目标索引加1 i++; } } if (i != h) { swap(arr,h,i); } System.out.println(Arrays.toString(arr)+"本轮基准点正确位置i:="+i); // 返回值代表基准点元素所在正确索引位置,用它确定下一轮分区的边界 return i; } // 交换方法 public static void swap(int[] arr,int i,int j) { int t = arr[i]; arr[i] = arr[j]; arr[j] = t; } }
执行效果