[2018蓝桥杯B组决赛] F-矩阵求和

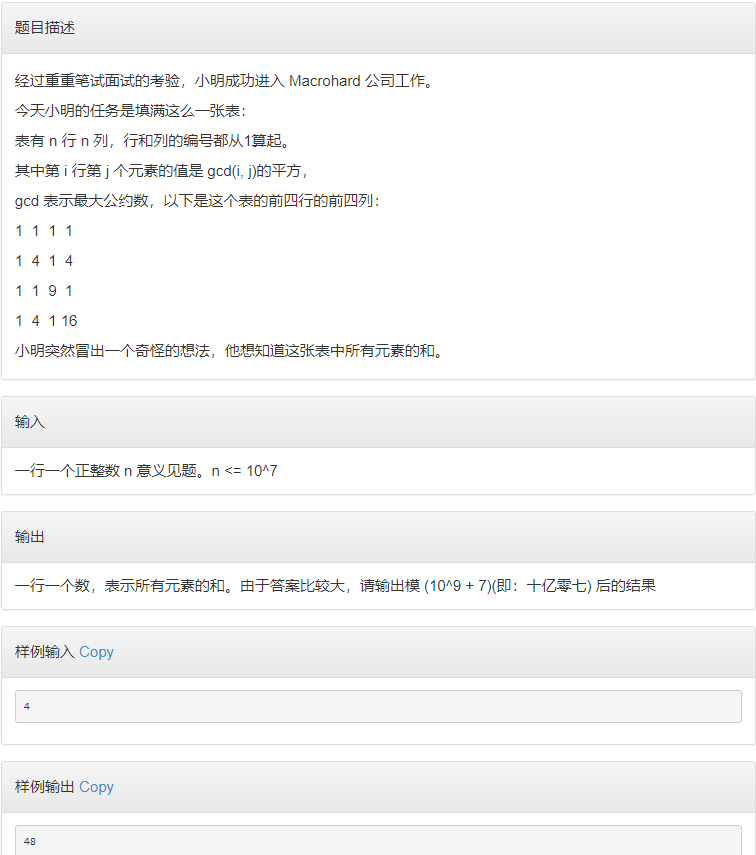
题解

　　依据数据范围，暴力枚举自然不可行，则应当转变思维。

　　gcd(i, j) = d 表示 (i, j) 的最大公约数为 d，而 count(d) 则表示最大公约数为 d 的数对的个数，count(d) * d * d 则求解的为最大公约数为 d 的所有数的和，此时问题的核心则转化为如何求 count(d)。

       $gcd(i, j) = d, gcd(\frac{i}{d}, \frac{j}{d}) = 1$。 

       令 $i = \frac{i}{d}, j = \frac{j}{d}$。

       代入则 $gcd(i, j) = 1$。

　　最大公约数的取值范围为 [1, n]，d 为 [1, n] 中的任意一个数。

       i, j 的取值在 [1, n / d]，求解该区间内所有互质对的个数， 而该题的数据范围比较大，故采用筛法求欧拉函数（线性筛法），即 1 - n 中的欧拉函数，时间复杂度能控制在 $O(n)$。

       

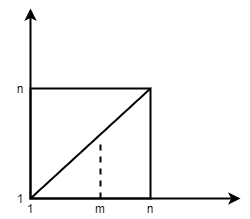
　　$s[n] = \sum_{i = 2}^n Euler(i) \times 2 + 1$ 

       上式可进行递推：

       $s[i] = s[i - 1] + 2 \times Euler[i]$

#include <iostream>
using namespace std;

typedef long long LL;
const int N = 1e7 + 10, mod = 1e9 + 7;
int n, cnt;
LL primes[N], eulers[N], s[N];
bool st[N];

// 线性筛法 
void get_eulers(int n)
{ 
    eulers[1] = 1;
    for (int i = 2; i <= n; ++i) {
        if (!st[i]) {
            primes[cnt++] = i;
            // i 为质数 
            eulers[i] = i - 1;
        }
        // 筛非质数 
        for (int j = 0; primes[j] <= n / i; ++j) {
            int t = primes[j] * i;
            st[t] = true;
            if (i % primes[j] == 0) {
                eulers[t] = eulers[i] * primes[j];
                break;
            }
            eulers[t] = eulers[i] * (primes[j] - 1);
        }
    }
    // 开 LL，避免溢出  
    s[1] = 1; 
    // 递推求解 s[i]
    for (int i = 2; i <= n; ++i) {
        s[i] = s[i - 1] + 2 * eulers[i];
    } 
}

int main()
{
    cin >> n;
    get_eulers(n);
    int res = 0;
    for (int d = 1; d <= n; ++d) {
        res = (res + (LL) s[n / d] * d % mod * d) % mod;
    }
    cout << res << endl;
    return 0;
}