redis zset底层数据结构
参考：
https://blog.csdn.net/xp178171640/article/details/102977210
https://www.cnblogs.com/lfls/p/7864798.html
https://www.cnblogs.com/aspirant/p/11475295.html
https://www.jianshu.com/p/fb7547369655
跳跃表原理
跳表(SkipList)：增加了向前指针的链表叫做指针。跳表全称叫做跳跃表，简称跳表。跳表是一个随机化的数据结构，实质是一种可以进行二分查找的有序链表。跳表在原有的有序链表上增加了多级索引，通过索引来实现快速查询。跳表不仅能提高搜索性能，同时也可以提高插入和删除操作的性能。
跳表是一个随机化的数据结构，可以被看做二叉树的一个变种，它在性能上和红黑树、AVL树不相上下，但是跳表的原理非常简单，目前在Redis和LevelDB中都有用到。
2、跳表的详解
说明：本文中的图片均来自极客时间《数据结构与算法之美专栏》对于一个单链表来说，即使链表中的数据是有序的，如果我们想要查找某个数据，也必须从头到尾的遍历链表，很显然这种查找效率是十分低效的，时间复杂度为O(n)。
那么我们如何提高查找效率呢？我们可以对链表建立一级“索引”，每两个结点提取一个结点到上一级，我们把抽取出来的那一级叫做索引或者索引层，如下图所示，down表示down指针。
假设我们现在要查找值为16的这个结点。我们可以先在索引层遍历，当遍历索引层中值为13的时候，通过值为13的结点的指针域发现下一个结点值为17，因为链表本身有序，所以值为16的结点肯定在13和17这两个结点之间。然后我们通过索引层结点的down指针，下降到原始链表这一层，继续往后遍历查找。这个时候我们只需要遍历2个结点（值为13和16的结点），就可以找到值等于16的这个结点了。如果使用原来的链表方式进行查找值为16的结点，则需要遍历10个结点才能找到，而现在只需要遍历7个结点即可，从而提高了查找效率。
那么我们可以由此得到启发，和上面建立第一级索引的方式相似，在第一级索引的基础上，每两个一级索引结点就抽到一个结点到第二级索引中。再来查找值为16的结点，只需要遍历6个结点即可，从而进一步提高了查找效率。
上面举得例子中的数据量不大，所以即便加了两级索引，查找的效率提升的也不是很明显，下面通过一个64结点的链表来更加直观的感受下索引提升查找效率，如图所示，建立了五级索引。
从图中我们可以看出来，原来没有索引的时候，查找62需要遍历62个结点，现在只需要遍历11个结点即可，速度提高了很多。那么，如果当链表的长度为10000、10000000时，通过构件索引之后，查找的效率就会提升的非常明显。
3、跳表的时间复杂度
单链表的查找时间复杂度为：O(n)，下面分析下跳表这种数据结构的查找时间复杂度：
我们首先考虑这样一个问题，如果链表里有n个结点，那么会有多少级索引呢？按照上面讲的，每两个结点都会抽出一个结点作为上一级索引的结点。那么第一级索引的个数大约就是n/2，第二级的索引大约就是n/4，第三级的索引就是n/8，依次类推，也就是说，第k级索引的结点个数是第k-1级索引的结点个数的1/2，那么第k级的索引结点个数为：。
假设索引有h级，最高级的索引有2个结点，通过上面的公式，我们可以得到，从而可得：h =
。如果包含原始链表这一层，整个跳表的高度就是
。我们在跳表中查找某个数据的时候，如果每一层都要遍历m个结点，那么在跳表中查询一个数据的时间复杂度就为：O(m*logn)。
其实根据前面的分析，我们不难得出m=3，即每一级索引都最多只需要遍历3个结点，分析如下：
如上图所示，假如我们要查找的数据是x，在第k级索引中，我们遍历到y结点之后，发现x大于y，小于y后面的结点z。所以我们通过y的down指针，从第k级索引下降到第k-1级索引。在第k-1级索引中，y和z之间只有3个结点(包含y和z)。所以，我们在k-1级索引中最多需要遍历3个结点，以此类推，每一级索引都最多只需要遍历3个结点。
因此，m=3，所以跳表查找任意数据的时间复杂度为O(logn)，这个查找的时间复杂度和二分查找是一样的，但是我们却是基于单链表这种数据结构实现的。不过，天下没有免费的午餐，这种查找效率的提升是建立在很多级索引之上的，即空间换时间的思想。其具体空间复杂度见下文详解。【面试题：如何让链表的元素查询接近线性时间】
4、跳表的空间复杂度
比起单纯的单链表，跳表就需要额外的存储空间去存储多级索引。假设原始链表的大小为n，那么第一级索引大约有n/2个结点，第二级索引大约有4/n个结点，依次类推，每上升一级索引结点的个数就减少一半，直到剩下最后2个结点，如下图所示，其实就是一个等比数列。
这几级索引结点总和为：n/2 + n/4 + n/8 + ... + 8 + 4 + 2 = n - 2。所以跳表的空间复杂度为O(n)。也就是说如果将包含n个结点的单链表构造成跳表，我们需要额外再用接近n个结点的存储空间。
其实从上面的分析，我们利用空间换时间的思想，已经把时间压缩到了极致，因为每一级每两个索引结点就有一个会被抽到上一级的索引结点中，所以此时跳表所需要的额外内存空间最多，即空间复杂度最高。其实我们可以通过改变抽取结点的间距来降低跳表的空间复杂度，在其时间复杂度和空间复杂度方面取一个综合性能，当然也要看具体情况，如果内存空间足够，那就可以选择最小的结点间距，即每两个索引结点抽取一个结点到上一级索引中。如果想降低跳表的空间复杂度，则可以选择每三个或者每五个结点，抽取一个结点到上级索引中。
如上图所示，每三个结点抽取一个结点到上一级索引中，则第一级需要大约n/3个结点，第二级索引大约需要n/9个结点。每往上一级，索引的结点个数就除以3，为了方便计算，我们假设最高一级的索引结点个数为1，则可以得到一个等比数列，去下图所示：
通过等比数列的求和公式，总的索引结点大约是：n/3 + n /9 + n/27 + ... + 9 + 3 + 1 = n/2。尽管空间复杂度还是O(n)，但是比之前的每两个结点抽一个结点的索引构建方法，可以减少了一半的索引结点存储空间。
实际上，在软件开发中，我们不必太在意索引占用的额外空间。在讲数据结构的时候，我们习惯性地把要处理的数据看成整数，但是在实际的软件开发中，原始链表中存储的有可能是很大的对象，而索引结点只需要存储关键值和几个指针，并不需要存储对象，所以当对象比索引结点大很多时，那索引占用的额外空间就可以忽略了。
5、跳表的插入
跳表插入的时间复杂度为：O(logn)，支持高效的动态插入。
在单链表中，一旦定位好要插入的位置，插入结点的时间复杂度是很低的，就是O(1)。但是为了保证原始链表中数据的有序性，我们需要先找到要插入的位置，这个查找的操作就会比较耗时。
对于纯粹的单链表，需要遍历每个结点，来找到插入的位置。但是对于跳表来说，查找的时间复杂度为O(logn)，所以这里查找某个数据应该插入的位置的时间复杂度也是O(logn)，如下图所示：
6、跳表的删除
跳表的删除操作时间复杂度为：O(logn)，支持动态的删除。
在跳表中删除某个结点时，如果这个结点在索引中也出现了，我们除了要删除原始链表中的结点，还要删除索引中的。因为单链表中的删除操作需要拿到删除结点的前驱结点，然后再通过指针操作完成删除。所以在查找要删除的结点的时候，一定要获取前驱结点（双向链表除外）。因此跳表的删除操作时间复杂度即为O(logn)。
7、跳表索引动态更新
当我们不断地往跳表中插入数据时，我们如果不更新索引，就有可能出现某2个索引节点之间的数据非常多的情况，在极端情况下，跳表还会退化成单链表，如下图所示：
作为一种动态数据结构，我们需要某种手段来维护索引与原始链表大小之间的平衡，也就是说，如果链表中的结点多了，索引结点就相应地增加一些，避免复杂度退化，以及查找、插入和删除操作性能的下降。
如果你了解红黑树、AVL树这样的平衡二叉树，你就会知道它们是通过左右旋的方式保持左右子树的大小平衡，而跳表是通过随机函数来维护“平衡性”。
当我们往跳表中插入数据的时候，我们可以通过一个随机函数，来决定这个结点插入到哪几级索引层中，比如随机函数生成了值K，那我们就将这个结点添加到第一级到第K级这个K级索引中。如下图中要插入数据为6，K=2的例子：
随机函数的选择是非常有讲究的，从概率上讲，能够保证跳表的索引大小和数据大小平衡性，不至于性能的过度退化。至于随机函数的选择，见下面的代码实现过程，而且实现过程并不是重点，掌握思想即可。
8、跳表的性质
(1) 由很多层结构组成，level是通过一定的概率随机产生的；
(2) 每一层都是一个有序的链表，默认是升序 ；
(3) 最底层(Level 1)的链表包含所有元素；
(4) 如果一个元素出现在Level i 的链表中，则它在Level i 之下的链表也都会出现；
(5) 每个节点包含两个指针，一个指向同一链表中的下一个元素，一个指向下面一层的元素。
聊聊Mysql索引和redis跳表 ---redis的有序集合zset数据结构底层采用了跳表原理 时间复杂度O(logn)(阿里)
redis使用跳表不用B+数的原因是：redis是内存数据库，而B+树纯粹是为了mysql这种IO数据库准备的。B+树的每个节点的数量都是一个mysql分区页的大小(阿里面试)
还有个几个姊妹篇：介绍mysql的B+索引原理 参考：一步步分析为什么B+树适合作为索引的结构 以及索引原理 (阿里面试)
参考：kafka如何实现高并发存储-如何找到一条需要消费的数据(阿里)
参考：二分查找法：各种排序算法的时间复杂度和空间复杂度(阿里)
关于mysql 存储引擎 介绍包括默认的索引方式参考：MySql的多存储引擎架构, 默认的引擎InnoDB与 MYISAM的区别(滴滴 阿里)
敲黑板：
每级遍历 3 个结点即可，而跳表的高度为 h ，所以每次查找一个结点时，需要遍历的结点数为 3*跳表高度 ，所以忽略低阶项和系数后的时间复杂度就是 ○(㏒n),空间复杂度是O(n)
| 数据结构 | 实现原理 | key查询方式 | 查找效率 | 存储大小 | 插入、删除效率 |
|---|---|---|---|---|---|
| Hash | 哈希表 | 支持单key | 接近O(1) | 小，除了数据没有额外的存储 | O(1) |
| B+树 | 平衡二叉树扩展而来 | 单key,范围，分页 | O(Log(n) | 除了数据，还多了左右指针，以及叶子节点指针 | O(Log(n)，需要调整树的结构，算法比较复杂 |
| 跳表 | 有序链表扩展而来 | 单key，分页 | O(Log(n) | 除了数据，还多了指针，但是每个节点的指针小于<2,所以比B+树占用空间小 | O(Log(n)，只用处理链表，算法比较简单 |
对LSM结构感兴趣的可以看下cassandra vs mongo (1)存储引擎
问题
如果对以下问题感到困惑或一知半解，请继续看下去，相信本文一定会对你有帮助
- mysql 索引如何实现
- mysql 索引结构B+树与hash有何区别。分别适用于什么场景
- 数据库的索引还能有其他实现吗
- redis跳表是如何实现的
- 跳表和B+树，LSM树有和区别呢
解析
首先为什么要把mysql索引和redis跳表放在一起讨论呢，因为他们解决的都是同一种问题，用于解决数据集合的查找问题，即根据指定的key，快速查到它所在的位置（或者对应的value）
当你站在这个角度去思考问题时，还会不知道B+树索引和hash索引的区别吗
数据集合的查找问题
现在我们将问题领域边界划分清楚了，就是为了解决数据集合的查找问题。这一块需要考虑哪些问题呢
- 需要支持哪些查找方式，单key/多key/范围查找，
- 插入/删除效率
- 查找效率（即时间复杂度）
- 存储大小（空间复杂度）
我们看下几种常用的查找结构
hash
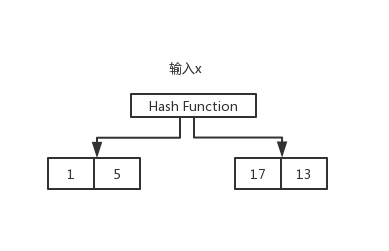
hash是key,value形式，通过一个散列函数，能够根据key快速找到value
关于hash算法 ，这也是阿里的必考题 深度的原理 我写了几篇博客：尤其是最后一篇resize ，以及resize之前与之后的hashmap的情况，
参考：Hashtable数据存储结构-遍历规则，Hash类型的复杂度为啥都是O(1)-源码分析
参考：HashMap, HashTable，HashSet,TreeMap 的时间复杂度
参考：HashMap底层实现原理/HashMap与HashTable区别/HashMap与HashSet区别
参考：ConcurrentHashMap原理分析（1.7与1.8）-put和 get 两次Hash到达指定的HashEntry
resize 参考：HashMap多线程并发问题分析-正常和异常的rehash1(阿里)
B+ 树：
注意 这是关于B+树的总结，如果你掌握到这个程度 是远远不够的，
请参考详细的B+树原理：一步步分析为什么B+树适合作为索引的结构 以及索引原理 (阿里面试)
B+树 的数据都在叶子节点，非叶子节点存放 索引
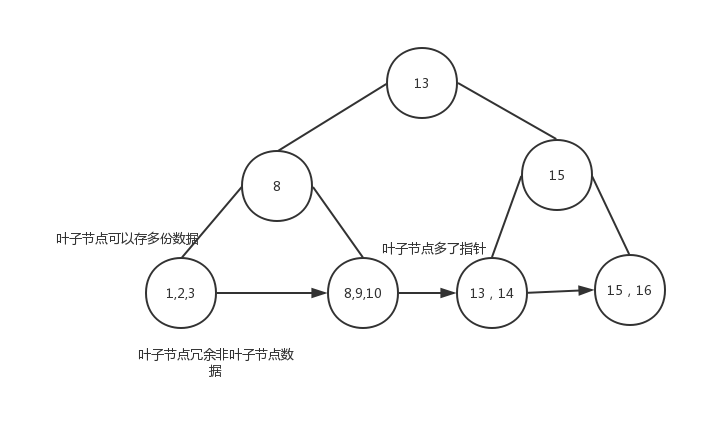
B+树是在平衡二叉树基础上演变过来，为什么我们在算法课上没学到B+树和跳表这种结构呢。因为他们都是从工程实践中得到，在理论的基础上进行了妥协。
B+树首先是有序结构，为了不至于树的高度太高，影响查找效率，在叶子节点上存储的不是单个数据，而是一页数据，提高了查找效率，而为了更好的支持范围查询，B+树在叶子节点冗余了非叶子节点数据，为了支持翻页，叶子节点之间通过指针连接。
跳表
跳表：为什么 Redis 一定要用跳表来实现有序集合？
上几篇主要是学习二分查找算法，但是二分查找底层依赖的是数组随机访问的特性，所以只能用数组来实现。如果数据存储在链表中，就没办法使用二分查找了吗？
此时跳表出现了，跳表（Skip list） 实际上就是在链表的基础上改造生成的。
跳表是一种各方面性能都比较优秀的 动态数据结构，可以支持快速的插入、删除、查找操作，写起来也不复杂，甚至可以替代 红黑树？？。
Redis 一共有5种数据结构，包括：
1、字符串(String)
redis对于KV的操作效率很高，可以直接用作计数器。例如，统计在线人数等等，另外string类型是二进制存储安全的，所以也可以使用它来存储图片，甚至是视频等。
2、哈希(hash)
存放键值对，一般可以用来存某个对象的基本属性信息，例如，用户信息，商品信息等，另外，由于hash的大小在小于配置的大小的时候使用的是ziplist结构，比较节约内存，所以针对大量的数据存储可以考虑使用hash来分段存储来达到压缩数据量，节约内存的目的，例如，对于大批量的商品对应的图片地址名称。比如：商品编码固定是10位，可以选取前7位做为hash的key,后三位作为field，图片地址作为value。这样每个hash表都不超过999个，只要把redis.conf中的hash-max-ziplist-entries改为1024，即可。
3、列表(List)
列表类型，可以用于实现消息队列，也可以使用它提供的range命令，做分页查询功能。
4、集合(Set)
集合，整数的有序列表可以直接使用set。可以用作某些去重功能，例如用户名不能重复等，另外，还可以对集合进行交集，并集操作，来查找某些元素的共同点
5、有序集合(zset)
有序集合，可以使用范围查找，排行榜功能或者topN功能。
其中第五个zset 有序集合 就是用跳表来实现的。那 Redis 为什么会选择用跳表来实现有序集合呢？
一、如何理解跳表？
对于单链表来说，我们查找某个数据，只能从头到尾遍历链表，此时时间复杂度是 ○(n)。
那么怎么提高单链表的查找效率呢？看下图，对链表建立一级 索引，每两个节点提取一个结点到上一级，被抽出来的这级叫做 索引 或 索引层。
开发中经常会用到一种处理方式，hashmap 中存储的值类型是一个 list，这里就可以把索引当做 hashmap 中的键，将每 2 个结点看成每个键对应的值 list。
所以要找到13，就不需要将16前的结点全遍历一遍，只需要遍历索引，找到13，然后发现下一个结点是17，那么16一定是在 [13,17] 之间的，此时在13位置下降到原始链表层，找到16，加上一层索引后，查找一个结点需要遍历的结点个数减少了，也就是说查找效率提高了
那么我们再加一级索引呢？
跟前面建立一级索引的方式相似，我们在第一级索引的基础上，每两个结点就抽出一个结点到第二级索引。此时再查找16，只需要遍历 6 个结点了，需要遍历的结点数量又减少了。
当结点数量多的时候，这种添加索引的方式，会使查询效率提高的非常明显、
二、用跳表查询到底有多快
在一个单链表中，查询某个数据的时间复杂度是 ○(n)，那在一个具有多级索引的跳表中，查询某个数据的时间复杂度是多少呢？
按照上面的示例，每两个节点就抽出一个一级索引，每两个一级索引又抽出一个二级索引，所以第一级索引的结点个数大约就是 n/2，第二级索引的结点个数就是 n/4，第 k 级索引的结点个数就是 n/2^k。
假设一共建立了 h 级索引，最高级的索引有两个节点（如果最高级索引只有一个结点，那么这一级索引起不到判断区间的作用，那么是没什么意义的），所以有：
根据上图得知，每级遍历 3 个结点即可，而跳表的高度为 h ，所以每次查找一个结点时，需要遍历的结点数为 3*跳表高度 ，所以忽略低阶项和系数后的时间复杂度就是 ○(㏒n)
其实此时就相当于基于单链表实现了二分查找。但是这种查询效率的提升，由于建立了很多级索引，会不会很浪费内存呢？
三、跳表是不是很浪费内存？
来分析一下跳表的空间复杂度。 为O(n)
所以如果将包含 n 个结点的单链表构造成跳表，我们需要额外再用接近 n 个结点的存储空间，那怎么才能降低索引占用的内存空间呢？
前面是每两个结点抽一个结点到上级索引，如果我们每三个，或每五个结点，抽一个结点到上级索引，是不是就不用那么多索引结点了呢？
计算空间复杂度的过程与前面的一致，尽管最后空间复杂度依然是 ○(n)，但我们知道，使用大○表示法忽略的低阶项或系数，实际上同样会产生影响，只不过我们为了关注高阶项而将它们忽略。
实际上，在实际开发中，我们不需要太在意索引占据的额外空间，在学习数据结构与算法时，我们习惯的将待处理数据看成整数，但是实际开发中，原始链表中存储的很可能是很大的对象，而索引结点只需要存储关键值（用来比较的值）和几个指针（找到下级索引的指针），并不需要存储原始链表中完整的对象，所以当对象比索引结点大很多时，那索引占用的额外空间就可以忽略了。
四、高效的动态插入和删除
跳表这个动态数据结构，不仅支持查找操作，还支持动态的插入、删除操作，而且插入、删除操作的时间复杂度也是 ○(㏒n)。
对于单纯的单链表，需要遍历每个结点来找到插入的位置。但是对于跳表来说，因为其查找某个结点的时间复杂度是 ○(㏒n)，所以这里查找某个数据应该插入的位置，时间复杂度也是 ○(㏒n)。
那么删除操作呢？
五、跳表索引动态更新
当我们不停的往跳表中插入数据时，如果我们不更新索引，就可能出现某 2 个索引结点之间数据非常多的情况。极端情况下，跳表会退化成单链表。
跳表是通过随机函数来维护前面提到的 平衡性。
我们往跳表中插入数据的时候，可以选择同时将这个数据插入到第几级索引中，比如随机函数生成了值 K，那我们就将这个结点添加到第一级到第 K 级这 K 级索引中。
跳表的实现有点复杂，并且跳表的实现并不是这篇的重点。主要是学习思路。
六、解答开篇
Redis 中的有序集合是通过跳表来实现的，严格点讲，还用到了散列表（关于散列表），如果查看 Redis 开发手册，会发现 Redis 中的有序集合支持的核心操作主要有下面这几个：
- 插入一个数据
- 删除一个数据
- 查找一个数据
- 按照区间查找数据（比如查找在[100,356]之间的数据）
- 迭代输出有序序列
其中，插入、查找、删除以及迭代输出有序序列这几个操作，红黑树也能完成，时间复杂度和跳表是一样的，但是，按照区间来查找数据这个操作，红黑树的效率没有跳表高。
对于按照区间查找数据这个操作，跳表可以做到 ○(㏒n) 的时间复杂度定位区间的起点，然后在原始链表中顺序往后遍历就可以了。这样做非常高效。
当然，还有其他原因，比如，跳表代码更容易实现，可读性好不易出错。跳表更加灵活，可以通过改变索引构建策略，有效平衡执行效率和内存消耗。
不过跳表也不能完全替代红黑树。因为红黑树出现的更早一些。很多编程语言中的 Map 类型都是用红黑树来实现的。写业务的时候直接用就行，但是跳表没有现成的实现，开发中想用跳表，得自己实现。
redis zset底层数据结构
zset底层存储结构
zset底层的存储结构包括ziplist或skiplist，在同时满足以下两个条件的时候使用ziplist，其他时候使用skiplist，两个条件如下：
- 有序集合保存的元素数量小于128个
- 有序集合保存的所有元素的长度小于64字节
当ziplist作为zset的底层存储结构时候，每个集合元素使用两个紧挨在一起的压缩列表节点来保存，第一个节点保存元素的成员，第二个元素保存元素的分值。
当skiplist作为zset的底层存储结构的时候，使用skiplist按序保存元素及分值，使用dict来保存元素和分值的映射关系。
ziplist数据结构
ziplist作为zset的存储结构时，格式如下图，细节就不多说了，我估计大家都看得懂，紧挨着的是元素memeber和分值socore，整体数据是有序格式。
skiplist作为zset的存储结构，整体存储结构如下图，核心点主要是包括一个dict对象和一个skiplist对象。dict保存key/value，key为元素，value为分值；skiplist保存的有序的元素列表，每个元素包括元素和分值。两种数据结构下的元素指向相同的位置。
skiplist的源码格式
zset包括dict和zskiplist两个数据结构，其中dict的保存key/value，便于通过key(元素)获取score(分值)。zskiplist保存有序的元素列表，便于执行range之类的命令。
/*
* 有序集合
*/
typedef struct zset {
// 字典，键为成员，值为分值
// 用于支持 O(1) 复杂度的按成员取分值操作
dict *dict;
// 跳跃表，按分值排序成员
// 用于支持平均复杂度为 O(log N) 的按分值定位成员操作
// 以及范围操作
zskiplist *zsl;
} zset;
zskiplist作为skiplist的数据结构，包括指向头尾的header和tail指针，其中level保存的是skiplist的最大的层数。
/*
* 跳跃表
*/
typedef struct zskiplist {
// 表头节点和表尾节点
struct zskiplistNode *header, *tail;
// 表中节点的数量
unsigned long length;
// 表中层数最大的节点的层数
int level;
} zskiplist;
skiplist跳跃列表中每个节点的数据格式，每个节点有保存数据的robj指针，分值score字段，后退指针backward便于回溯，zskiplistLevel的数组保存跳跃列表每层的指针。
/*
* 跳跃表节点
*/
typedef struct zskiplistNode {
// 成员对象
robj *obj;
// 分值
double score;
// 后退指针
struct zskiplistNode *backward;
// 层
struct zskiplistLevel {
// 前进指针
struct zskiplistNode *forward;
// 跨度
unsigned int span;
} level[];
} zskiplistNode;
zset存储过程
zset的添加过程我们以zadd的操作作为例子进行分析，整个过程如下：
- 解析参数得到每个元素及其对应的分值
- 查找key对应的zset是否存在不存在则创建
- 如果存储格式是ziplist，那么在执行添加的过程中我们需要区分元素存在和不存在两种情况，存在情况下先删除后添加；不存在情况下则添加并且需要考虑元素的长度是否超出限制或实际已有的元素个数是否超过最大限制进而决定是否转为skiplist对象。
- 如果存储格式是skiplist，那么在执行添加的过程中我们需要区分元素存在和不存在两种情况，存在的情况下先删除后添加，不存在情况下那么就直接添加，在skiplist当中添加完以后我们同时需要更新dict的对象。
void zaddGenericCommand(redisClient *c, int incr) {
static char *nanerr = "resulting score is not a number (NaN)";
robj *key = c->argv[1];
robj *ele;
robj *zobj;
robj *curobj;
double score = 0, *scores = NULL, curscore = 0.0;
int j, elements = (c->argc-2)/2;
int added = 0, updated = 0;
// 输入的 score - member 参数必须是成对出现的
if (c->argc % 2) {
addReply(c,shared.syntaxerr);
return;
}
// 取出所有输入的 score 分值
scores = zmalloc(sizeof(double)*elements);
for (j = 0; j < elements; j++) {
if (getDoubleFromObjectOrReply(c,c->argv[2+j*2],&scores[j],NULL)
!= REDIS_OK) goto cleanup;
}
// 取出有序集合对象
zobj = lookupKeyWrite(c->db,key);
if (zobj == NULL) {
// 有序集合不存在，创建新有序集合
if (server.zset_max_ziplist_entries == 0 ||
server.zset_max_ziplist_value < sdslen(c->argv[3]->ptr))
{
zobj = createZsetObject();
} else {
zobj = createZsetZiplistObject();
}
// 关联对象到数据库
dbAdd(c->db,key,zobj);
} else {
// 对象存在，检查类型
if (zobj->type != REDIS_ZSET) {
addReply(c,shared.wrongtypeerr);
goto cleanup;
}
}
// 处理所有元素
for (j = 0; j < elements; j++) {
score = scores[j];
// 有序集合为 ziplist 编码
if (zobj->encoding == REDIS_ENCODING_ZIPLIST) {
unsigned char *eptr;
// 查找成员
ele = c->argv[3+j*2