【字符串匹配】KMP算法板子
KMP
- 在text串中找有无pattern子串
- 参考:如何更好地理解和掌握 KMP 算法? - 海纳的回答 - 知乎 https://www.zhihu.com/question/21923021/answer/281346746
匹配
- 部分匹配表(Partial Match Table, PMT)的数组:qmt[i-1]表示字符串前i个字符(s[0]~s[i-1])的前缀与后缀重复的部分的长度为qmt[i-1]那么长。
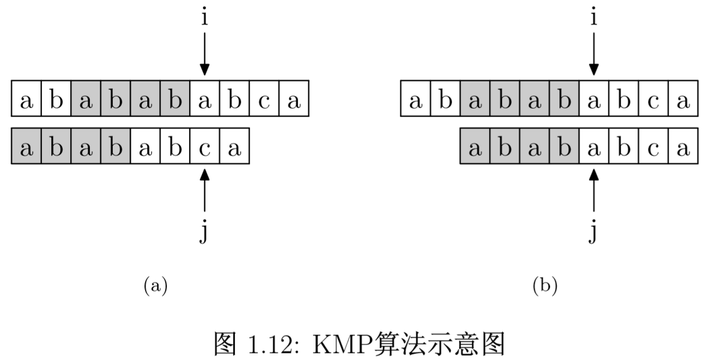
- 在下图中qmt[i-1] = 4
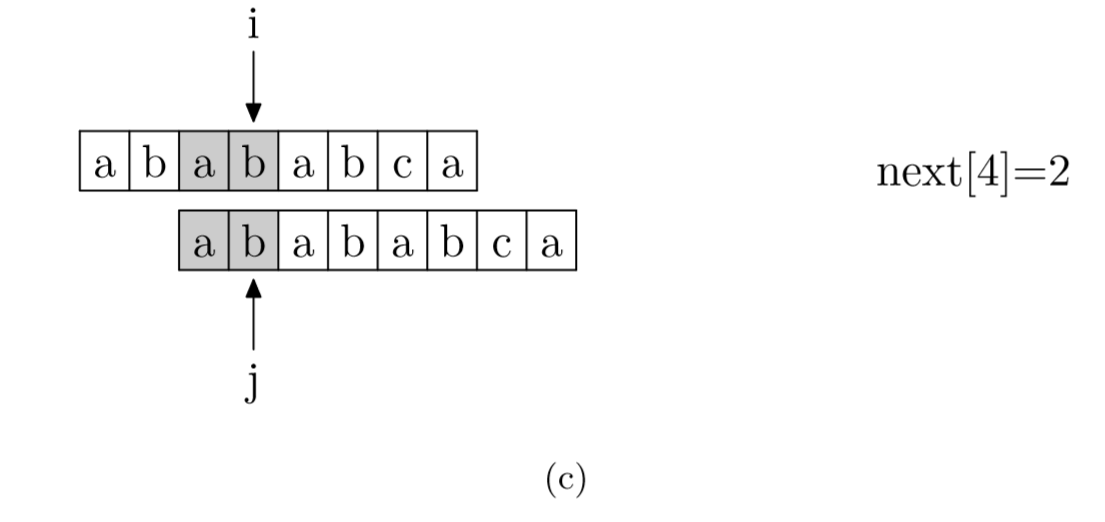
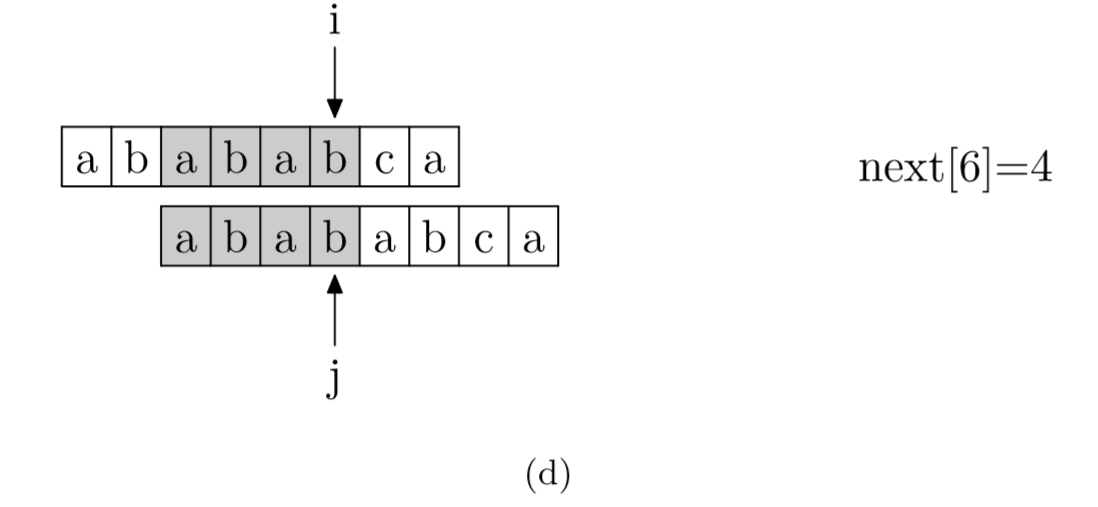
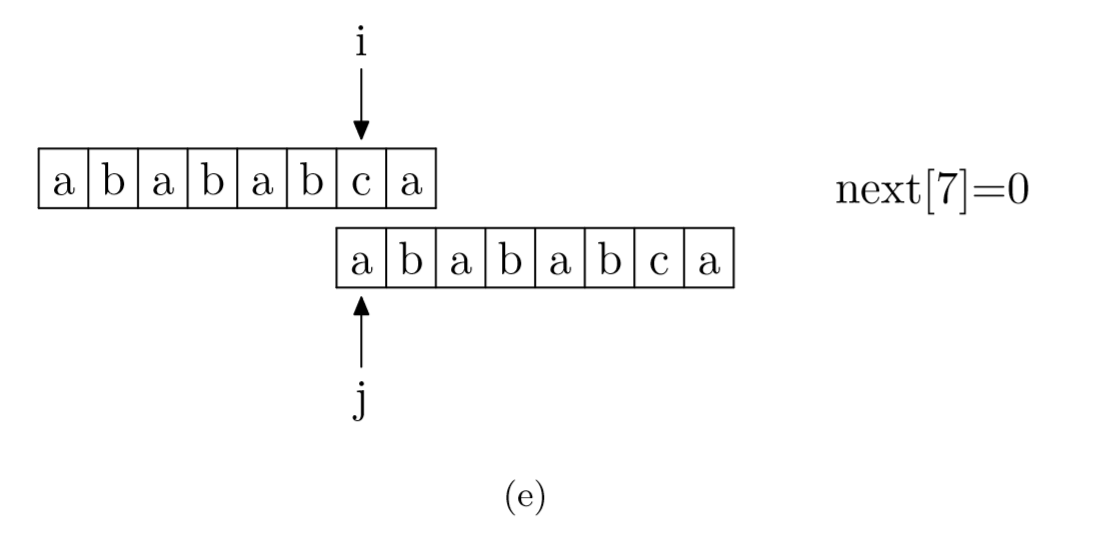
- 当text[i]与pattern[j]不匹配时,i指针前j个字符都匹配上了。
- 根据PMT的定义,pattern中 j前pmt[j-1]个字符与pattern中从0开始的pmt[j-1]的字符是一样的。
- 所以不需要再从头匹配,pattern的j指针直接跳转到pmt[j-1]即可继续匹配
求next数组
-
由于在j位失配,那么影响j指针回溯位置的其实是j-1的PMT值。
-
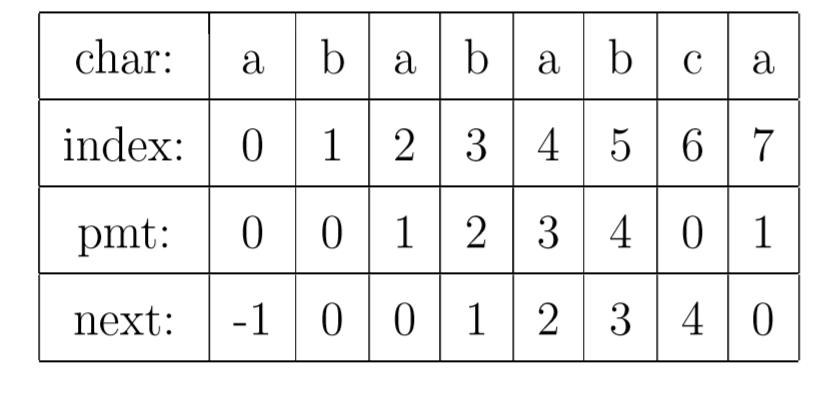
所以为了编程方便,将PMT数组向后偏移一位,得到新数组next数组。
-
由于偏移了,所以next数组的下标是从0到strlen(pattern)的,有strlen(pattern)+1个元素,而不止strlen(pattern)个
-
这样在j位失配后,直接跳转到next[j]即可(比pmt[j-1]方便)
-
第0位的next值为-1:为了编程方便
-
-
-
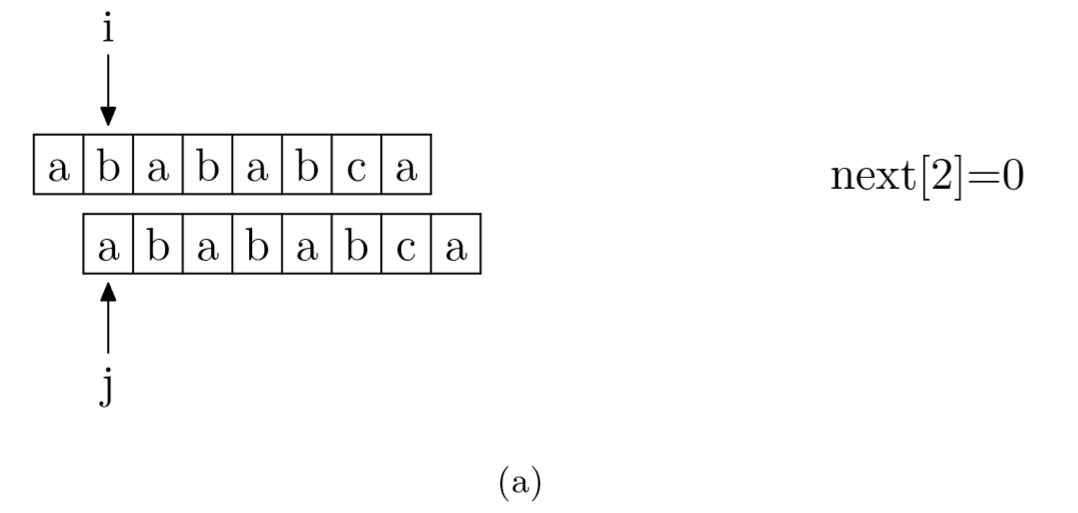
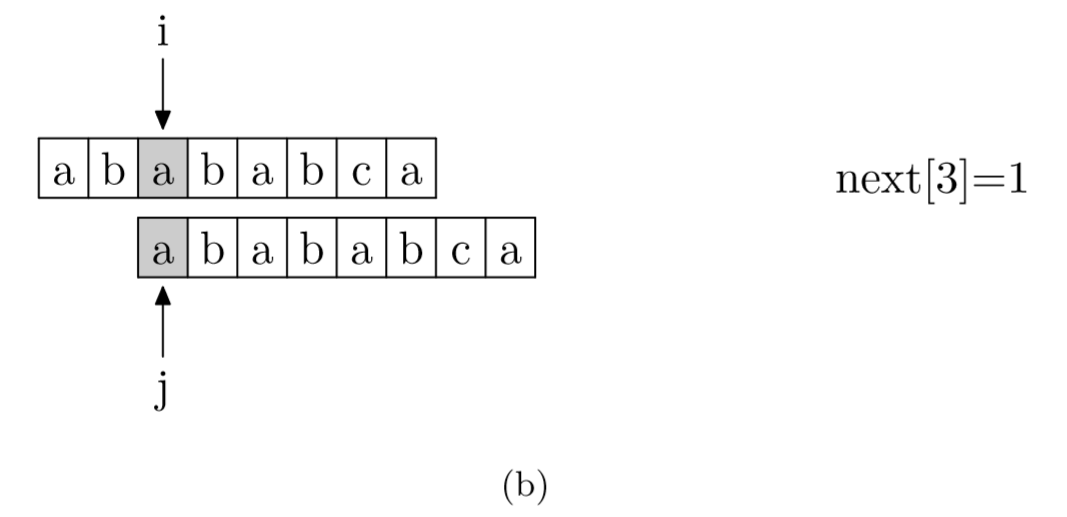
求next数组:其实就是pattern与pattern匹配
-
-
-
-
-
模板
void getNext(char * p, int * nxt){
nxt[0] = -1;
int i=0, j=-1;
// 注意这里跳出的条件是i==strlen(p)
// 所以其实只要扫一遍pattern就可以求出nxt数组
// 要区别kmp
while(i<strlen(p)){
if(j==-1||p[i]==p[j]){
// 注意是先自增再赋值nxt数组
// 这样可以让pmt偏移一位成为nxt
j++;
i++;
nxt[i] = j;
}
else{
j = nxt[j];
}
}
}
int kmp(char * t, char * p){
int i = 0;
int j = 0;
while(i<strlen(t)&&j<strlen(p)){
// 注意在kmp和getNext中都要判断j是否为-1
// 即使kmp中j初始值的初始值为0
// 但是在j = nxt[j]中,nxt[0]=-1
// j也可能会-1
// 如果没加上这个条件,可能会导致RE
if(j==-1||t[i]==p[j]){
i++;
j++;
}
else j = nxt[j];
}
// 匹配完了pattern
// 返回在text中找到的起始位置
// 注意这里的pattern和text的下标都是从0开始的
if(j==strlen(p)){
return i-j;
}
// 找不到返回-1
else return -1;
}

