NN&DL复习
NN&DL复习
-
两种基本范式:监督学习,无监督学习。
-
监督学习:\(\{(x^{(i)},y^{(i)})\}\), 有标签。
- 寻找一个映射H: X->Y,使得H(x)是一个好的分类器。
- 输入新的x,可以得到一个正确的预测标签y。
-
无监督学习:
- 给数据集\(\{x^{i};i=1,..,m\}\)
- 目标:将这些数据归为不同的Cluster
- 没有给y
- 根据数据间的相似性来归类。
-
对比 分类 聚类 是否有标签 有 无 数据获取的难度和数据量 有限,费时费力 大量,无处不在 难度 如果有大量标注好的数据,不算太难 有时挺困难
-
-
损失函数
- 0-1损失函数
- \(L(y,f(x;\theta))=0\ if\ y=f(x;\theta)\)
- \(L(y,f(x;\theta))=1\ if\ y\ !=\ f(x;\theta)\)
- 平方损失函数\(L(y,\hat y)=(f-f(x;\theta))^2\)
- 负对数损失函数\(L(y,p(y|x))=-logp(y|x)\)
- 0-1损失函数
-
代价函数:定义在整个训练集上的
- 均方误差MSE \(MSE=\frac 1 N \sum_{i=1}^N(y-f(x^{(i)}))^2\)
- 交叉熵代价函数 cross-entropy loss function: \(H(p,q)=-\sum_Cp(x)log q(x)=-\sum_{c=1}^Cy_clogf_c(x;\theta)=-logf_y(x;\theta)\)
-
目标函数:一般是经验风险+结构风险(代价函数+正则化项)
-
强化学习(不考)
线性模型
-
一定要掌握:四种模型(线性回归,感知机,逻辑回归,Softmax分类)
-
线性回归
-
\(f(x)=w^Tx+b\)
-
梯度下降
- 原理:利用MSE作为目标函数\(MSE=\frac1{2m}\sum_{i=1}^m(y^{(i)}-f(x^{(i)}))^2\)
- 公式:
- \(b:= b-\alpha \frac1m\sum_{i=1}^m(f(x^{(i)})-y^{(i)})\)
- \(w:=w-\alpha\frac1m\sum_{i=1}^m(f(x^{(i)})-y^{(i)})*x^{(i)}\)
- 迭代方法
- 有哪些参数
-
最小二乘法
-
最小二乘法和梯度下降适用于什么样的场景,有什么优缺点。
-
梯度下降法 最小二乘法 SGD 选择学习率 需要 不需要 需要 迭代求解 是 否 是 特征数m很大时 不影响 计算速度很慢 高效率
-
-
逻辑回归
- 分类模型,二分类,推广了的感知机,它的激活函数(符号函数)替换成了Logistic函数(sigmoid),从-1/1这样的分类器1变成了给出类别隶属度的概率(属于某类的概率)。
- Logistic函数
- 不是回归模型
- 损失函数:交叉熵函数
-
感知机
- 分类模型(二分类的线性模型)
- 输入是实例的特征向量,输出类别:+1 and -1
- 激活函数为sign函数
- \(f(x)=sign(w*x+b)\)
- 损失函数:期望使误分类的所有样本,到超平面的距离之和最小
- 梯度
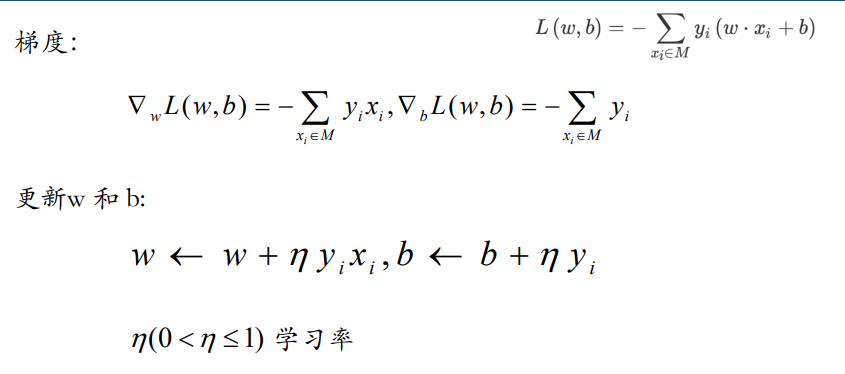
- 更新
-
采用什么损失函数
-
多分类:softmax
- 是Logistic回归的多类推广
- 交叉熵:\(R(W)=-\frac{1}{N}\sum_{n=1}^N(y^{(n)})^Tlog\hat y^{(n)}\)
- 交叉熵损失\(L(y,f(x,\theta))\)
-
掌握 会写softmax
-
采用不同的损失函数的原因
- 极大似然推导
深度神经网络 深度前馈网络
- (重点)BP算法
- 熟练掌握
- 目标函数
- 自己实现
- 什么叫净输入,每层输出。
- 最后一层的梯度更新和中间层的梯度更新
- 和\(\delta\)有关
- 熟练掌握
卷积神经网络CNN
- 什么是卷积
- 一维卷积:\(y_t=\sum^m_{k=1}w_k*x_{t-k+1}\)
- \(w\): filter(滤波器)即 convolutional kernel(卷积核)
- \(y\): feature map (特征图谱)
- 二维卷积:\(y=w\otimes x\), \(y_{ij}=\sum^m_{u=1}\sum^n_{v=1}w_{uv}\cdot x_{i-u+1,j-v+1}\)
- 为什么要CNN?
- 视觉世界的四个特性:
- 局部不变性:像素与像素之间,主要与其附近的像素有关,而与其距离较远的像素无关。
- 统计平稳性:像素的统计性指标在整幅图像中是相对统一的
- 平移(旋转、缩放)不变性:对于物体的识别不依赖于它在图像中的位置
- 构成性:被识别目标是由各个部分构成的。
- 而全连接前馈网络很难提取这些局部不变特征。
- 视觉世界的四个特性:
- 为什么要卷积神经网络,比深度前馈网络。适用于什么样的场景。
- CNN四个结构上的特性
- 局部卷积计算(小的局部感受野):局部不变性(洗漱交互,通过让filter比输入小来实现的)
- 参数共享(权重共享):统计平稳性
- 层次叠加(感受野随着网络加深而增大):被识别目标是由各部分组成的(更深层次的单元可能会间接地与更大的输入部分交互)
- 空间或时间上的池化(下采样):平移不变性
- 这些特性使得CNN具有一定程度上的平移、缩放和扭曲不变性。
- CNN四个结构上的特性
- 会算卷积
- 给你卷积核的大小,要会算输出的feature map多大
- 输入大小:\(W \times W\)
- Filter大小:\(F \times F\)
- 步长:S
- 零填充大小:P
- 输出(Feature Map):\(N\times N, N=\frac{W-F+2P}{S}+1\)
- 注:每组filter出一个feature map
- 注意有没有padding,零填充
- ex: padding p=1,若是1维array则第一个和最后一个加0,若是2维则加一圈0。
- 注意步长
- 给你卷积核的大小,要会算输出的feature map多大
- 卷积神经网络的优点,缺点,适用场景
- 池化pooling的作用
- (可以看作是添加了一个无限强的先验假设,即每一个单元都具有少量平移保持不变)
- 对微小平移的不变性
- 更大的接受域
- 池化:滑动步长标准做法是平铺——无重叠滑动
- 卷积的两种说法(卷积网络是由卷积层、池化层、全连接层交叉堆叠而成)
- 卷积和池化一起 ( input-> [convolution stage, detector stage, pooling stage] -> next layer)
- 卷积和池化分开 (input->convolutional stage -> detector layer -> pooling layer -> next layer)
循环神经网络
- 适用,擅长什么样的数据
- 适合于序列建模任务
- 更新公式
- 输入数据:\(x_t\)
- 隐藏单元状态更新:\(h_t=tanh(W_{hh}h_{t-1}+w_{xh}x_t)\)
- 输出: \(\hat y_t=W_{hy}h_t\)
- 循环神经网络按照时间步展开是什么样子
- 循环神经网络的梯度下降算法
- BPTT back propagation through time
- 采用BPTT之后,求梯度:w有连乘
- 梯度消失:可以通过设计新的网络结构来缓解
- 梯度爆炸:可以通过梯度截断来控制
- 二者本质是什么:推导部份,连乘部份,w<1, w>1
- 梯度消失: w<1, RNN面临的主要问题
- 梯度爆炸:w>1, 梯度值会变成NaN,采取梯度截断的方法,当梯度大于某一阈值时,将梯度进行缩减。
- 解决梯度消失的模型
- LSTM:通过附加一些门控机制来改善梯度的流动,大大缓解了梯度消失的问题
- 几个简化图
- GRU怎么来的:了解一下,只有重置门和更新门
- ESN:了解一下
- LSTM:通过附加一些门控机制来改善梯度的流动,大大缓解了梯度消失的问题
- 掌握:RNN和LSTM
自编码器
- 无监督学习
- 监督信号来自本身
- 根据重构误差惩罚网络
- 最重要的在bottleneck部份(瓶颈要比输入输出小)
- 适当的约束中间隐变量的维度,浓缩
- 容量不宜过大,防止网络对输入的简单拷贝而无法学习得到有用的信息。
- 理解:
- 降噪编码器:属于正则自编码器
- 对输入略微增加噪声,通过训练之后得到无噪声的输出
- 防止了自编码器简单的讲输入复制到输出,从而提取出数据中有有用的模式
- 正则自编码器:对网络采用各形式的正则化,以鼓励更好的泛化属性。
- 正则自编码器包括:稀疏自编码器,去噪自编码器
- 稀疏自编码器:
- 节点的不透明度与激活级别对应。稀疏自编码器将根据输入数据选择性地激活网络区域,达到稀疏正则化的效果。
- 稀疏性约束的实现方式,如L1正则化
- 提供一种不需要减少隐藏层的节点数量,就可以引入信息瓶颈的方法。
- 使隐藏层中相对独立的结点对特定的输入特征或者属性变得更加敏感。
- 稀疏自编码器:
- 降噪编码器:属于正则自编码器
- 不足:只能重构样本,无法生成新的样本——生成新的样本用生成模型(VAE、GAN)
深度生成模型
- 什么是生成模型 :从某个分布中获取输入训练样本,并学习表示该分布的模型。
- 掌握VAE和GAN的基本原理
VAE(变分自编码器)
- VAE理解,概率化的自编码器
- VAE使传统自编码器的概率版本,是一种生成模型,可以生成数据。
- 通过显式地对样本的概率密度建模(借助隐变量),随后通过最大化变分下界来近似样本的概率密度。
- VAE相当于在AE的重构损失基础上,加入了一个KL散度的正则化项。
- VAE的思路,有很好的数学模型
- 要理解其变分下界
GAN(生成式对抗网络)
- GAN基本原理
- 从一些简单的分布中采样数据,例如随机噪声,学习一个随机噪声到训练数据分布的变换。
- 采用博弈论方法。
- 生成器:将随机噪声变换为模仿的假样本,试图欺骗判别器。
- 判别器:要从真实样本和生成器生成的样本中识别真实样本。
- 生成器,判别器两者关系
- GAN的目标函数要熟悉
- 通过极大极小博弈来联合训练GAN
- \(min_{\theta_g}max_{\theta_d}[E_{x~pdata}logD_{theta_d}(x)+E_{z~p(z)}log(1-D_{\theta_d}(G_{\theta_g}(z)))]\)
- 判别器要最大化目标函数,让\(D_{|theta_d}(x)\)接近1,而\(D_{\theta_d}(G_{\theta_g}(z))\)接近0。判别器输出的是(0,1)的概率值。
- 生成器要最小化目标函数,让\(D_{\theta_d}(G_{\theta_g}(z))\)接近1
正则化
- L1,L2正则化的原理,起的作用
- L1正则:\(||W||_1=\sum_i|w_i|\),最小化\(||W||_1\)
- 起到更加稀疏解的作用
- L1正则化图形(等值线)有角,因此与它的彩色线(没有正则化目标的等值线)的交点很可能是在这些“角”点上。
- L2(权重衰减、岭回归):\(||w||^2_2\), 最小化\(||w||^2_2\)
- 其导数为2W。
- 将权重按照其大小比例缩减,使权重更加接近原点。
- L2正则化图形(等值线)没有角,因此它与彩色线的交点不太可能在某个坐标轴上。
- L1正则:\(||W||_1=\sum_i|w_i|\),最小化\(||W||_1\)
- 如何提高深度学习的泛化性能的手段
- 增加优化约束
- L1,L2正则化
- 数据增强:通过算法对图像进行转变,引入噪声等方法来增加数据的多样性。
- 旋转、翻转、缩放、平移、加噪声。
- 干扰优化过程
- 提前终止:用一个测试集来测试每一次迭代的参数在验证集上是否最优。如果在验证集上的错误率不再下降,就停止迭代。
- Dropout:对一个神经层\(y=f(Wx+b)\),引入一个丢弃函数\(d(\cdot)\)使得\(y=f(Wd(x)+b)\)
- \(d(x)=m\odot x\)(当训练阶段时), \(m \in \{0,1\}^d\)是丢弃掩码,通过以概率为p的伯努利分布随机生成。
- \(d(x)=px\) (当测试阶段时)
- 使得任何隐藏单元都不能依赖于其他隐藏单元
- 每做一次丢弃,相当于从原始的网络中采样得到一个子网络也就是可以达到多个网络集成学习的效果。
- ex: 假设dropout rate 为0.5(正好一半隐藏单元丢弃了),4个隐藏单元,我们得到\(C_4^2=6\), 相当于6个子网络集成。
- 权重衰减
- 随机梯度下降
- 等等
- 增加优化约束
优化
- 对于学习率自适应的优化
- AdaGrad
- AdaDelta
- RMSprop
- AdaGrad
- 对于梯度更新方向自适应的优化
- 动量法:用之前积累动量来替代真正的梯度。每次迭代的梯度都可以看作是加速度。
- \(\triangle \theta_t=ρ\triangle \theta_t - \alpha g_t=-\alpha \sum_{T=1}^t \beta^{t-T}g_T\)
- 动量法:用之前积累动量来替代真正的梯度。每次迭代的梯度都可以看作是加速度。
- 梯度方向优化+自适应学习率
- Adam算法≈动量法+RMSprop
- 了解深度学习各个模型的进展

