凸集 凸函数 凸优化 概念
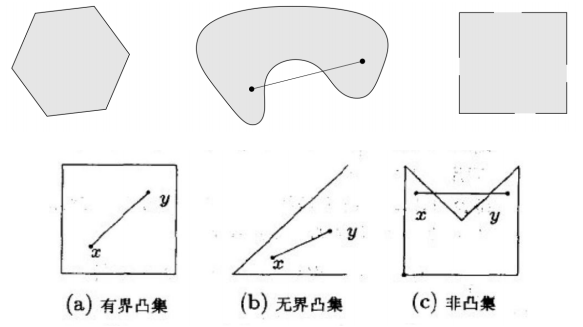
凸集
-
集合C内任意两点间的线段也均在集合C内，则称集合C为凸集。
-
\(\forall x_1, x_2 \in C, \forall \theta \in [0,1], 则 x= \theta * x_1 + (1-\theta)*x_2 \in C\)\
-
凸函数定义
-
f为定义在区间I上的函数，若对I上的任意两点\(x_i, x_2\)和任意\(\lambda \in (0,1)\) 有\(f(\lambda x_i + (1-\lambda)x_2)\leq \lambda f(x_i)+(1-\lambda)f(x_2)\)
-
将\(\leq\)换成<也成立则严格凸函数。
几个性质
-
性质1： 设 \(f ⊆ R^n–> R^1\)，C是凸集，若f是凸函数，则对于∀β，证明下面水平集\(D_β\)是凸集。 \(D_\beta = \{x|f(x) \leq \beta, x \in C\}\)
-
性质2 : 凸优化问题的局部极小值是全局极小值。
-
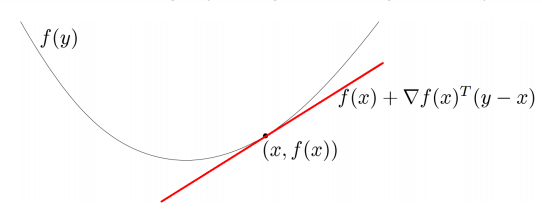
性质3： 若f一阶可微，则函数f为凸函数当且仅当f的定义域domf为凸集，且 \(\forall x,y \in domf, f(y)\geq f(x) + \triangledown f(x)^T(y-x)\)
-
性质4：若f二阶可微，则函数f为凸函数当且仅当f的定义域domf为凸集，且\(\triangledown ^2f(x)\succeq 0\)
- 若f为一元函数，上式表示二阶导大于0
- 若f为多元函数，上式表示二阶导Hessian矩阵半正定。
Hessian矩阵
- 即二阶导数矩阵
- 多元函数的Hessian矩阵
- hessian矩阵正定：
- 函数的二阶偏导数恒>0
- 函数的变化率（一阶导数）始终处于递增状态
- 函数为凸
正定 半正定
-
正定：\(f(x_1,x_2,...,x_n)=x^TAx\)，（所有的二次齐次式都可以写成这个形式）如果对任意的\(x \neq 0\)均有\(f(x)>0\)，则称\(f(x)\)为正定二次型，同时称\(A\)为正定矩阵。
-
正定：对于n阶实对称矩阵A，下列条件是等价的：
- A是正定矩阵；
- A的一切顺序主子式均为正；
- A的一切主子式均为正；
- A的特征值均为正；
- 存在实可逆矩阵C，使A=C′C；
- 存在秩为n的m×n实矩阵B，使A=B′B；
- 存在主对角线元素全为正的实三角矩阵R，使A=R′R
-
半正定：设A是n阶实对称矩阵，则下列的条件等价：
1.A是半正定的。
2.A的所有主子式均为非负的。
3.A的特征值均为非负的。
4.存在n阶实矩阵C，使A=C′C.
5.存在秩为r的r×n实矩阵B，使A=B′B.
凸优化问题
-
OPT，convex optimization problem，凸集中的凸函数最优化的问题。
-
基本形式：\(minimize\ f_0(x), x\in R^n\)
\(subject\ to\ f_i(x)\leq0,i=1...m; h_(x)=0,j=1...p\)
-
优化变量 \(x\in R^n\)
-
不等式约束 \(f_i(x)\leq 0\)
-
等式约束 \(h_j(x)=0\)
-
无约束优化 \(m=p=0\)
-
优化问题的域 \(D=\cap_{i=0}^m domf \cap \cap_{j=1}^p domh_j\)
-
可行点（解）：\(x\in D\)，且满足约束条件
-
可行域：所有可行点的集合
-
最优化值 \(p^* = inf\{f_0(x)|f_i(x)\leq0,i=1...m,h_j(x)=0,j=1...p\}\)
-
最优化解 \(p^*=f_0(x^*)\)
-
凸优化问题的重要性质：
- 可行域为凸集
- 局部最优解即全局最优解
