主席树学习心得

主席树是用于处理区间第k大(小)的问题

对于一个序列，想要知道[l,r]区间内第k大(小)的数，考虑建一颗权值线段树，这样我们就可以解决一个定区间的第k大问题了，假如我现在有两颗权值线段树，分别维护了[1，l-1]，[1，r]两个区间，这样要解决[l，r]区间的问题，就是两个权值线段树节点值作差，就可以得到一颗维护[l，r]的权值线段树了，那么，如何对于1<=l,r<=n的区间得到对应的维护[l,r]的权值线段树呢？显然我们只需维护所有的[1，i]，1<=i<=n，这样我们可以通过作差得到任意维护[l，r]区间的权值线段树了，然而，建立n个权值线段树，它的时间空间花费都是无法接受的，不过，我们可以发现，相邻的两颗权值线段树，他们只有一条链是存在差异的，也就是说，我们从维护[1，i]的权值线段树，变成[1，i+1]的权值线段树，只需额外开辟logn的空间，这样，我们创建两个指针，一个指向前一颗权值线段树的根，另外一颗指向当前生成的权值线段树的根，如果新加入的数，只会影响前一颗权值线段树的右儿子(左儿子同理)，那么我们让当前生成的权值线段树，左儿子指向前一颗权值线段树的左儿子，然后为右儿子开辟新节点，两个指针同时下移到他们的右儿子，进行递归处理即可，这样我们就构造了一颗主席树，这就是动态开点的过程

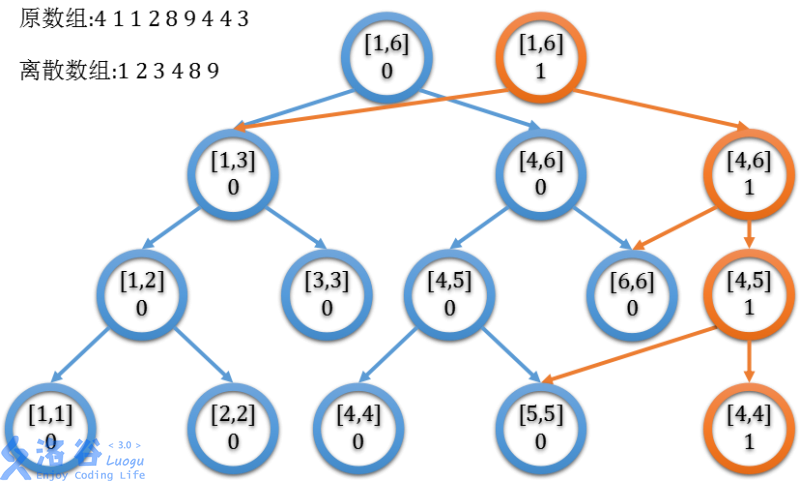（图源洛谷）

建立主席树后，查询[l，r]的区间第k大(小问题)就变成了在主席树上查询[1，l-1]，与[1，r]两颗权值线段树的问题了，我们通过两个指针，从两个根节点开始访问，同步地访问左/右子树

当左子树权值差lsum大于k，说明第k小的元素就在左子树中，否则我们递归访问右子树，第k小要变成第k-lsum（它在右子树是第k-lsum小的）这样，我们就轻易地解决了区间第k小问题

主席树模板(静态第k小，无区间修改操作)

#include <bits/stdc++.h>
using namespace std;
const int N = 2e5+5;
struct Node
{
    int l,r,sum;
}node[N*40];//nlogn
int cnt;
int a[N],root[N];
void Insert(int l,int r,int pre,int& now,int val)
{
    node[++cnt]=node[pre];
    now=cnt;
    node[now].sum++;
    if(l==r)return;
    int m=(l+r)>>1;
    if(val<=m)Insert(l,m,node[pre].l,node[now].l,val);
    else Insert(m+1,r,node[pre].r,node[now].r,val);
}
vector<int>v;//需要离散化
inline int getId(int val)
{
    return lower_bound(v.begin(),v.end(),val)-v.begin()+1;
}
int queryKthMin(int l,int r,int L,int R,int k)
{
    if(l==r)return l;
    int m=(l+r)>>1;
    int lsum=node[node[R].l].sum-node[node[L].l].sum;
    if(k<=lsum)return queryKthMin(l,m,node[L].l,node[R].l,k);
    else return queryKthMin(m+1,r,node[L].r,node[R].r,k-lsum);
}
int main() {
    int n, m;
    ios::sync_with_stdio(false);
    cin >> n >> m;
    for (int i = 1; i <= n; i++) {
        cin >> a[i];
        v.push_back(a[i]);
    }
    sort(v.begin(), v.end());
    v.erase(unique(v.begin(), v.end()), v.end());
    for (int i = 1; i <= n; i++) {
        Insert(1, n, root[i - 1], root[i], getId(a[i]));
    }
    int l,r,k;
    while (m--) {
        cin>>l>>r>>k;
        cout<<v[queryKthMin(1,n,root[l-1],root[r],k)-1]<<'\n';
    }
    return 0;
}