堆排序

思路（大根堆）：

部分堆排序：

从某根节点开始，看左右孩子的值是否大于根节点。

若根节点不为最大值，找到左右孩子的最大值和根节点交换。

交换后破坏了下一级堆，则需要对下一级堆继续用以上方法排序。

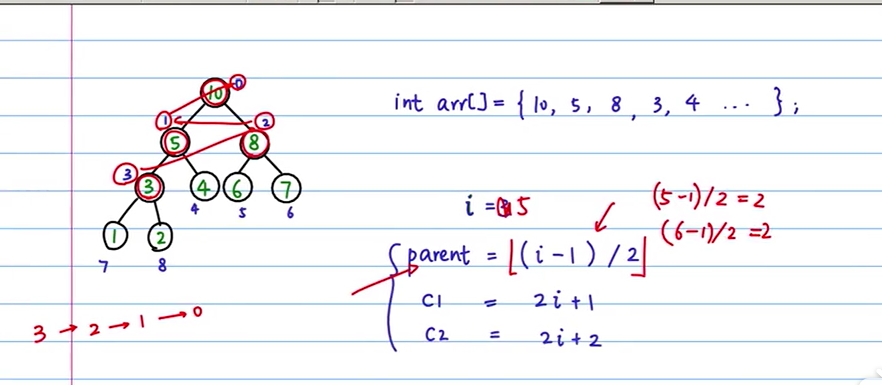
建立堆：

从最后一个节点开始，找到父节点，从父节点遍历到根节点，用堆排序，最后就建立一个排好序的堆。

空间复杂度：O(1)

时间复杂度：O(nlong2n)

是一种不稳定的排序方法

 

 

#include <iostream>
#include <stdlib.h>
#include <math.h>
#include <string.h> 
#include <algorithm>
using namespace std;
//int A[1000]={0,49,38,65,97,76,13,27,49,55,4};
//int A[]={4,10,3,5,1,2};
int A[]={10,3,2,4,1,6};
void heapSort(int n,int i){//n数组元素总数  i堆排序根节点  
    if(i>=n){
        return;
    }
    int c1=2*i+1;           //左孩子 且根节点序号从0开始  如果根节点序号从1开始  c1=2*i； 
    int c2=2*i+2;           //右孩子 且根节点序号从0开始  如果根节点序号从1开始  c2=2*i+1；
    int max=i;              //max记录根节点 左孩子 右孩子 中的最大值 
    if(c1<n&&A[c1]>A[max]){
        max=c1;
    }
    if(c2<n&&A[c2]>A[max]){
        max=c2;
    }
    if(i!=max){             //根节点不为最大值 该部分堆需要更新 
        int t=A[i];
        A[i]=A[max];
        A[max]=t;
        heapSort(n,max);    //由于根节点进行了更新 以此为根节点的子堆也需要更新 
    }
} 
void build_heap(int n){     //从最后开始建立堆 
    int last=n-1;           //最后一个节点 
    int parent=(last-1)/2;  //父节点 
    for(int i=parent;i>=0;i--){  
        heapSort(n,i);
    }
}
int main(){
    build_heap(6);
    for(int i=0;i<=5;i++){
        cout<<A[i]<<" ";
    }
    return 0;
}