(并查集)擒贼先擒王

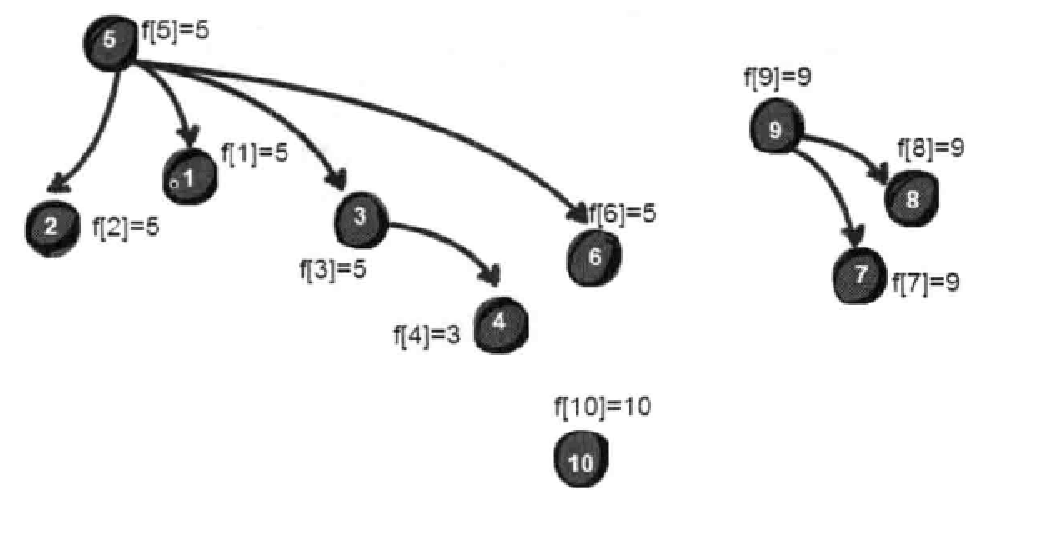
并查集是若干个集合，可以判断两个对象是否在一个集合中，从而判断它们需不需要进行一个操作。合并集合就是合并树，使两颗树指向同一个祖先节点。

 

 理解就是某下标对应的数组值存的是父节点的下标值

有若n个强盗 有m个线索，每个线索中的两个强盗为同伙（倘若A与B是同伙，B与C是同伙，那么A与C也是同伙），判断有多少个独立的犯罪团伙。

样例数据：

10 9//10个强盗 9条线索

1 2

3 4

5 2

4 6

2 6

8 7

9 7

1 6

2 4

输出样例:

3

 

 

#include <stdio.h>
#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
bool vis[105];
long long a[1005];
int n,m;
long long ans;
int getf(int v){                    //递归找 所在节点的boss 
    if(a[v]==v){                    //节点的值等于该序号 则是boss节点 
        return v;
    }
    else{
        a[v]=getf(a[v]);           //路径压缩 将每个节点的boss设置为 最终的boss值 
        return a[v];               //压缩后可以提高今后查找某节点最终boss（就是树祖先）的速度 
    }
}
void marge(int v,int u){           
    int t1=getf(v);
    int t2=getf(u);
    if(t1!=t2){                    //合并节点原则 右边向左边合并  即右边成为左边元素的子集  
        a[t2]=t1;
    }
}
int main() {
    cin>>n>>m;
    for(int i=1;i<=n;i++){           //初始化 设置每个节点的boss是自己 
        a[i]=i;
    } 
    int x,y;
    for(int i=1;i<=m;i++){
        cin>>x>>y;
        marge(x,y);                 //合并同伙 
    }
    for(int i=1;i<=n;i++){            //扫描数组 找boss 
        if(a[i]==i) ans++;
    }
    cout<<ans;
    return 0;
}