优化算法
优化算法
-
Batch梯度下降法每次对整个训练集进行计算,这在数据集很大时计算效率低下,因为每次更新权重前必须先处理整个训练集。
可以将训练集划分为多个小子集,称为mini-batch。每次只使用一个mini-batch来计算梯度并更新参数。取出 \(x^{(1)}\) 到 \(x^{(1000)}\),将其组成第一个mini-batch,记作 \(X^{\{1\}}\)。对应的标签 \(y^{(1)}\) 到 \(y^{(1000)}\) 记作 \(Y^{\{1\}}\)。接下来,依次取出 \(x^{(1001)}\) 到 \(x^{(2000)}\) 等,直到训练集被分成若干个mini-batch。
如果训练集共有 \(t\) 个mini-batch,则 \(X^{\{t\}}\) 是第 \(t\) 个子集样本矩阵,维度为 \((n_x, \text{mini-batch size})\)。 \(Y^{\{t\}}\) 是第 \(t\) 个子集标签矩阵,维度为 \((1, \text{mini-batch size})\)。
mini-batch梯度下降法每次训练会遍历 \(t\) 个mini-batch,每次更新包括:- 从训练集中取出一个mini-batch \(X^{\{t\}}\) 和 \(Y^{\{t\}}\) 并计算神经网络的预测值 \(A^{\{t\}}\) 以及当前的损失 \(J^{\{t\}}\)。如果使用正则化,计算公式为:
\[ J^{\{t\}} = \frac{1}{\text{mini-batch size}} \sum_{i=1}^{\text{mini-batch size}} L(\hat{y}^{(i)}, y^{(i)}) + \frac{\lambda}{2 \cdot \text{mini-batch size}} \sum_{l=1}^L ||W^{[l]}||_F^2 \]- 计算损失函数 \(J^{\{t\}}\) 对权重 \(W^{[l]}\) 和偏置 \(b^{[l]}\) 的梯度并根据学习率 \(\alpha\) 更新权重和偏置。
完成一整个训练集的遍历,可以称为1代(epoch),通常需要多次epoch来使模型收敛。当数据规模非常大时,mini-batch梯度下降法会比batch梯度下降法训练更快。
-
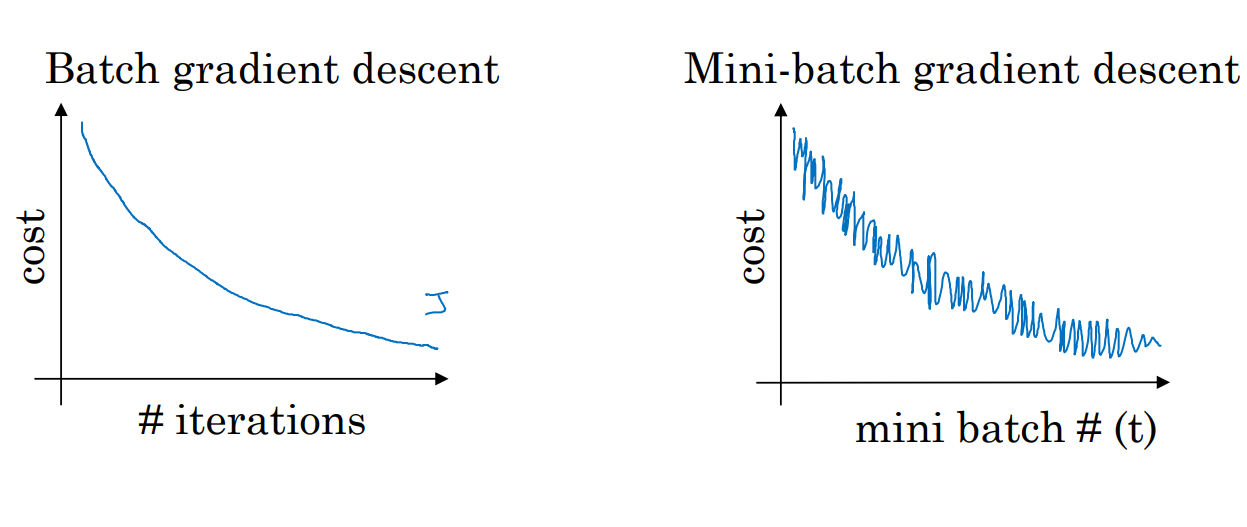
使用batch梯度下降法时,每次迭代都需要遍历整个训练集,因此每次迭代代价函数都会下降。
如果使用mini-batch梯度下降,每次迭代的代价函数并不一定是单调下降的,会存在很多的噪声,但整体趋势是下降的。
-
如果mini-batch size等于 \(m\),那么就等价于batch梯度下降法。这种情况下每次迭代处理整个数据集,计算开销大,单次迭代耗时过长,尤其是在样本数目巨大时。
如果mini-batch size等于1,那么就等价于随机梯度下降法。虽然每次迭代处理一个样本,计算开销小,但会丧失向量化的加速优势,且计算噪声较大,优化路径易波动且不收敛。
为综合计算效率和优化效果,mini-batch size通常选择一个介于1和 \(m\) 之间的值。
当样本数量小于2000时,直接使用batch梯度下降法即可,因处理整个数据集的开销较低,无需拆分成 mini-batch。
当样本数量较大时,mini-batch size一般取64,128,256,512这几个2的幂次方值,因为计算设备在处理这种尺寸时优化效果更好。
mini-batch size还应该适配硬件的CPU/GPU内存容量。如果 mini-batch size 超过内存限制,计算性能将严重下降,可能导致程序无法运行。实验时可以尝试不同的mini-batch size,观察哪个值能够以最高效率优化成本函数。
-
指数加权移动平均是一种平滑时间序列的方法,通过赋予近期数据点更大的权重,来计算一段时间内的均值,其公式为:
\[v_t=\beta v_{t-1}+(1-\beta)\theta_t \]其中 \(v_t\) 是第 \(t\) 时刻的加权平均值, \(\theta_t\) 是第 \(t\) 时刻的观测值, \(\beta\) 是平滑系数,取值范围为 \(0 \leq \beta < 1\),通常接近于1。
\(v_t\) 近似表示过去 \(\frac{1}{1-\beta}\) 个时刻的加权均值。 \(\beta\) 越大,平滑效果越显著,但响应新变化的速度会降低(曲线更平稳但滞后)。 \(\beta\) 越小,对数据变化会更敏感。
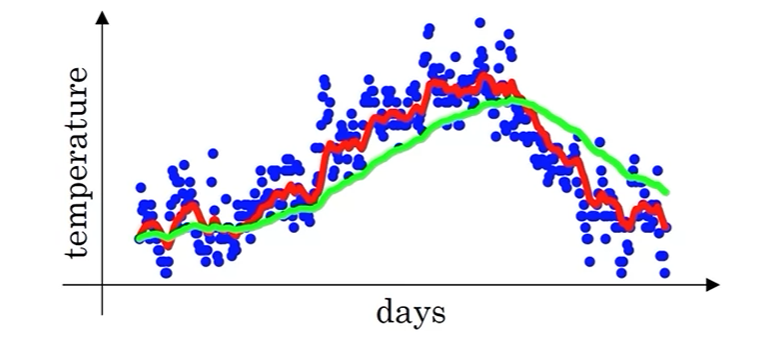
在代码中,可以通过以下循环公式逐步更新 \(v_t\):
\[v_{t}=\beta v_{t-1} + (1-\beta) \theta_t \]在一开始, \(v_0=0\),因此 \(v_1=(1-\beta)\theta_1\),会出现冷启动的问题。如图中紫色曲线所示,在一开始均值会明显低于正常值。
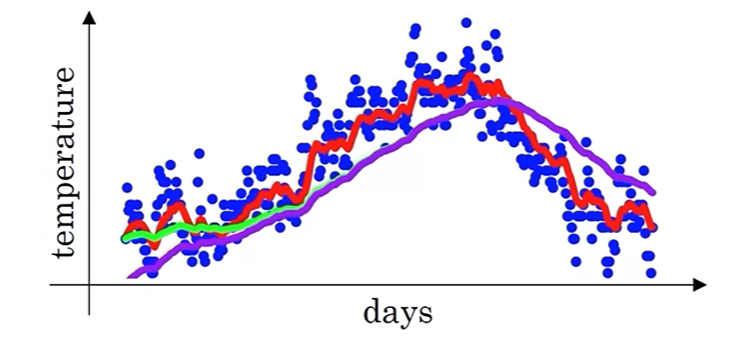
为了修正初始阶段的偏差,使用以下公式:
\[v_t=\frac{\beta v_{t-1}+(1-\beta)\theta_t}{1-\beta^t} \]其中修正项 \(1-\beta^t\) 随时间 \(t\) 增加逐渐趋近于 1,因此当 \(t\) 较大时,偏差修正的作用逐渐减弱。随时间推移,紫色曲线(真实均值曲线)逐渐与修正均值曲线(绿色)重合。
-
在优化某些狭长形状的成本函数时,梯度下降法会出现显著的震荡问题,尤其是在纵轴方向上(例如陡峭方向),这会减缓收敛速度。然而,横轴方向的梯度更新通常较为平稳,并符合优化的总体趋势。
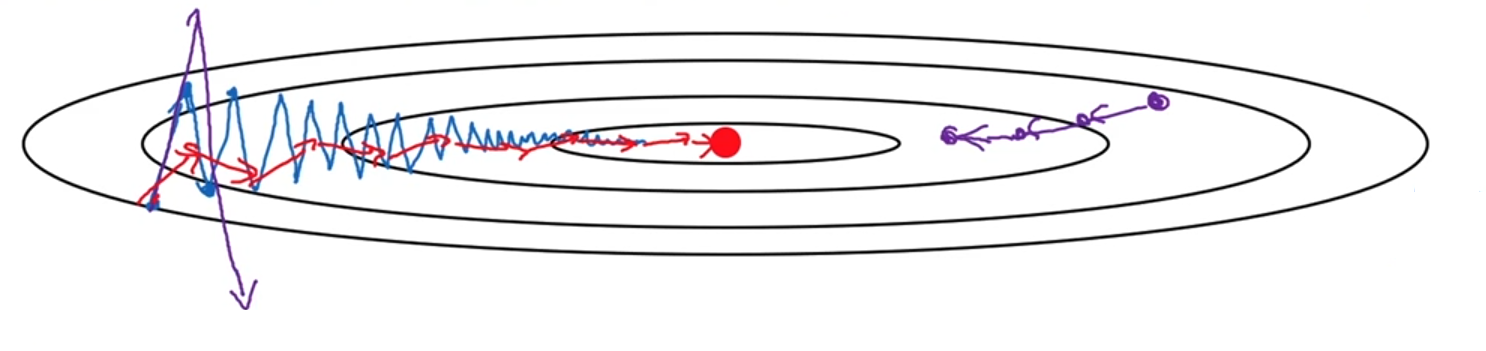
为了减小纵轴方向的震荡,同时保持横轴方向的学习趋势,动量梯度下降法(Momentum Gradient Descent)被提出。其核心思想是通过对历史梯度进行指数加权移动平均,消除震荡频繁的高频梯度分量(纵轴正负振荡相互抵消),从而加速收敛。
动量梯度下降法通过以下步骤更新参数:
\[\text{Compute dW,db on the current mini-batch} \\ V_{d\omega} = \beta V_{d\omega} + (1-\beta)d\omega \\ V_{db}= \beta V_{db} + (1-\beta)db \\ \omega = \omega - \alpha V_{dw} \quad b=b-\alpha V_{db} \]其中,\(\beta\) 为动量超参数,通常取值为 0.9。若优化过程中震荡较严重,可以稍微增大 \(\beta\);若优化过于平滑,可能需要降低 \(\beta\)。动量法中一般不对动量项进行偏差修正,因为影响较小。
在纵轴方向上,由于正负梯度交替,指数加权平均使动量值趋于零,从而显著减小震荡。在横轴方向上,梯度更新方向一致,动量叠加加速收敛。动量法的平滑效果使参数更新轨迹更加稳定,接近成本函数最优解时收敛速度更快。 -
除了动量梯度下降法外,均方根传滴(RMSProp)也可以加速梯度下降,通过自适应调整不同方向上的学习率,避免过大的更新步长,从而加速收敛。RMSProp 的关键思想是对每个参数的梯度平方进行指数加权移动平均,用于调整学习率的分母,使学习率在陡峭方向缩小,而在平缓方向保持较大。
RMSProp通过以下步骤更新参数:
\[\text{Compute dW,db on the current mini-batch} \\ S_{d\omega}=\beta_2S_{d\omega}+(1-\beta_2)d\omega^2 \\ S_{db}=\beta_2S_{db}+(1-\beta_2)db^2 \\ \omega = \omega -\alpha \frac{d\omega}{\sqrt{S_{d\omega}}+\epsilon} \\ b = b -\alpha \frac{db}{\sqrt{S_{db}}+\epsilon} \]这里的 \(\beta_2\) 为控制历史平均的超参数,但区分于动量梯度下降法中的超参数 \(\beta\) 。 \(\epsilon\) 是一个极小值,用于防止分母除零。
陡峭方向的梯度较大,其平方值在移动平均中占主导地位,使得分母较大,从而减小该方向上的更新步长,避免震荡。平缓方向的梯度较小,其平方值使分母较小,从而增大该方向的更新步长,加速收敛。
-
Adam(Adaptive Moment Estimation)自适应矩估计优化算法是一种结合了动量梯度下降法(Momentum)和均方根传递(RMSProp)思想的优化算法,具有两者的优点:动量法的加速收敛和平滑轨迹,以及 RMSProp 的自适应学习率调整。Adam 在深度学习中非常流行,因为它对超参数的依赖较少且具有良好的收敛性能,适用于稀疏梯度和高噪声问题。
Adam 同时维护两个变量:梯度的动量(第一矩估计),通过对梯度的指数加权平均,积累方向性信息,平滑优化过程。梯度平方的均值(第二矩估计),记录梯度平方的加权平均,自适应调整学习率大小。\[ V_{d\omega}=0 \quad S_{d\omega}=0 \quad V_{db}=0 \quad S_{db}=0 \\ \text{Compute dW,db on the current mini-batch} \\ V_{d\omega} = \beta_1 V_{d\omega} + (1-\beta_1)d\omega \\ V_{db}= \beta_1 V_{db} + (1-\beta_1)db \\ S_{d\omega}=\beta_2S_{d\omega}+(1-\beta_2)d\omega^2 \\ S_{db}=\beta_2S_{db}+(1-\beta_2)db^2 \\ V_{d\omega}^{\text{corrected}}=\frac{V_{d\omega}}{1-\beta_1^t} \quad V_{db}^{\text{corrected}}=\frac{V_{db}}{1-\beta_1^t} \\ S_{d\omega}^{\text{corrected}}=\frac{S_{d\omega}}{1-\beta_2^t} \quad S_{db}^{\text{corrected}}=\frac{S_{db}}{1-\beta_2^t} \\ \omega = \omega -\alpha \frac{V_{d\omega}^{\text{corrected}}}{\sqrt{S_{d\omega}^{\text{corrected}}}+\epsilon} \\ b = b -\alpha \frac{V_{db}^{\text{corrected}}}{\sqrt{S_{db}^{\text{corrected}}}+\epsilon} \]在Adam算法中,一般取 \(\beta_1=0.9\), \(\beta_2=0.999\), \(\epsilon=10^{-8}\)。
但是在某些情况下,Adam 的动态学习率可能导致未能找到最优解。而且Adam针对深度学习中的非凸目标更有效,但对于严格凸优化问题可能表现不如 SGD。
-
在深度学习中,学习率是控制每次参数更新步长的关键超参数。为了兼顾初期快速收敛和后期精细调整,学习率衰减被广泛应用。初期学习率较大,加速学习速度;随着训练的进行,学习率逐渐减小,从而在接近最优解时更稳定地优化目标函数。
常用的学习率衰减策略:-
基于迭代的衰减。学习率随着训练代数逐渐减小。
\[ \alpha = \frac{\alpha_0}{1 + \text{decayRate} \times \text{epochNumber}}. \]参数: \(\alpha_0\) 初始学习率, \(\text{decayRate}\) 学习率衰减率, \(\text{epochNumber}\) 当前训练代数。
-
指数衰减。学习率按指数规律衰减,简单易用,且衰减速度较快,适用于较短的训练过程。
\[\alpha = \alpha_0 \times \gamma^{\text{epochNumber}}, \quad \gamma < 1. \]\(\gamma\) 是衰减因子(例如 \(\gamma = 0.95\) 表示每轮训练学习率缩小为原来的 95%)。
-
分段衰减。在训练的特定阶段手动调整学习率。适合需要灵活控制学习率的场景,能够手动调整需要监控模型性能。
\[\alpha = \begin{cases} \alpha_0 & \text{if } \text{epochNumber} < \text{step1}, \\ \alpha_0 / k & \text{if } \text{step1} \leq \text{epochNumber} < \text{step2}, \\ \alpha_0 / k^2 & \text{if } \text{epochNumber} \geq \text{step2}. \end{cases} \] -
基于性能的学习率调整。通过监控模型性能(如验证集损失或精度)动态调整学习率。若验证集损失在一段时间内不下降,则减小学习率。
如果学习率衰减过快,可能导致模型在找到局部最优解前停止优化。如果学习率衰减过慢,可能会浪费计算资源,甚至陷入震荡。
-
-
在深度学习研究早期,人们担心优化算法会被困在局部最优值,无法找到全局最优值。这种直觉主要来源于低维空间的损失函数图像。在这些低维图像中,局部最优点分布广泛,优化算法可能停留在某个局部最优点无法跳出。
在高维空间(如 2 万维参数的神经网络)中,梯度为零的点并不一定是局部最优点,而是更有可能是鞍点。在某些方向是凸的(曲线向上弯曲),而在另一些方向是凹的(曲线向下弯曲)。在高维空间中,满足所有方向均为局部最优点的概率极低,甚至接近于 \(2^{-20000}\)。
平稳段是指梯度接近于零的一块区域。在这一区域内,优化算法会学习得非常缓慢。在平稳段中,算法需要依靠微弱的随机扰动(如噪声)才能走出平稳段,找到下坡的路径。
动量梯度下降(Momentum)、均方根传递(RMSProp)、Adam 等优化算法通过动态调整更新方向和步长,可以加速穿越平稳段。随机扰动和高维参数空间的特性也使得优化算法能够逐步摆脱平稳段,继续下降。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号