Leetcode 1-5题
两数之和
给定一个整数数组和一个目标值,在数组中找出和为目标值的两个整数,并返回其数组下标。题目确保必存在一个答案,且数组中无重复元素。
数组长度为\([2,10^4]\)
可以采用哈希表来存储每个值以及其出现的下标,那么对于nums[i]只需要查询在数组中是否出现过target-nums[i]即可。
如果存在则返回两个下标,否则将当前的数放入哈希表中。
采用unordered_map进行存储,最终时间复杂度为\(O(n)\)。
vector<int> twoSum(vector<int>& nums, int target) {
unordered_map<int, int> mp;
for(int i = 0; i < nums.size(); i ++) {
int num = nums[i];
if(mp.count(target - num)) return {i, mp[target - num]};
mp[num] = i;
}
return {};
}
两数相加
用两个非空的链表逆序存储两个非负整数,每个节点存储一位数字。将两个数相加,并返回结果链表,保证不含前导零。
数\(564\)表示为
4->6->5。
从个位开始将两个链表的每个节点相加,若结果大于9则产生进位,且在下一轮加法中需要加上进位。
循环的终止条件是已经遍历完两个链表,且最后一次加法的进位不为1。
在每次做完加法后,可以将结果存到新的链表节点中,最后返回头节点的下一个节点开始的链表。
否则如果更新当前元素的话,最后如果不加特判,会容易多一个\(0\)出来。算法时间复杂度为\(O(n)\)。
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
ListNode* addTwoNumbers(ListNode* l1, ListNode* l2) {
auto head = new ListNode(), current = head;
int t = 0; // 进位
while(l1 || l2 || t) {
if(l1) t += l1->val, l1 = l1->next;
if(l2) t += l2->val, l2 = l2->next;
current->next = new ListNode(t % 10); // 将结果存到下一个节点
t /= 10;
current = current->next;
}
return head->next; // 返回从第二个节点开始的链表
}
无重复字符的最长子串
给定字符串,求不含有重复字符的最长子串的长度。
若S[j..i]这一段内已经包含了重复字符,那么S[j..i+1]这一段内也会包含重复字符。
如果S[j.i]内无重复字符,但S[j..i+1]内有重复字符,那么必然是S[i+1]出现了不止一次。
可以使用哈希表来存储当前区间内每个字符出现的次数。
因此对于S[j..i+1]内有重复字符的情况,j必须右移到使得区间内无重复字符的位置,此时S[j..i+1]就是对S[i+1]而言最长的无重复字符的子串。
由于j一直是向右移动,所以具有单调性,双指针算法时间复杂度为\(O(n)\)。
int lengthOfLongestSubstring(string s) {
unordered_map<char, int> mp;
int res = 0;
for(int j = 0, i = 0; i < s.length(); i ++) {
mp[s[i]] ++;
while(mp[s[i]] > 1) { // 若重复则持续右移j
mp[s[j]] --;
j ++;
}
res = max(res, i - j + 1);
}
return res;
}
寻找两个正序数组的中位数
给定两个有序数组,返回这两个数组合并之后的中位数。要求时间复杂度为
O(log (m+n))。数组长度为\([0,1000]\)
首先,若m+n为奇数,则寻找第(m+n)/2个数,若为偶数,则寻找第(m+n)/2和(m+n)/2+1个数并求平均值。
将问题转化为如何求两个数组中第\(k\)小的数呢?
取两个数组的第\(\frac{k}{2}\)个元素,若\(A_{k/2}<B_{k/2}\),那么\(A[0..\frac{k}{2}-1]\)内的元素必然都不是第\(k\)小,便排除了这一部分。
接下来只需要在\(A[\frac{k}{2}+1..]\)和\(B\)中找第\(k-\frac{k}{2}\)个数即可。
int find(vector<int>& nums1, int i, vector<int>& nums2, int j, int k) {
int m = nums1.size(), n = nums2.size();
if(m - i > n - j) return find(nums2, j, nums1, i, k); // 让nums1为较短的数组
if(m - i == 0) return nums2[j + k - 1]; // 若nums1为空
if(k == 1) return min(nums1[i], nums2[j]); // 若要寻找最小的数直接返回较小值
int si = min(m, i + k / 2), sj = j + k - k / 2; // 注意nums1中选的位置不能超过数组长度m
if(nums1[si - 1] < nums2[sj - 1]) return find(nums1, si, nums2, j, k - (si - i));
else return find(nums1, i, nums2, sj, k - (sj - j));
}
double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {
int m = nums1.size(), n = nums2.size();
int k = (m + n) / 2;
if((m + n) % 2) return find(nums1, 0, nums2, 0, k + 1);
else return (find(nums1, 0, nums2, 0, k) + find(nums1, 0, nums2, 0, k + 1)) / 2.0;
}
最长回文子串
给定字符串,求字符串的最长回文子串。
字符串长度为\([1,1000]\)
由于字符串长度比较短,因此\(O(n^2)\)的算法可以过。
动态规划法
令\(P[i][j]\)表示\(S[i..j]\)是否是回文串,那么显然有P[i][j] = P[i+1][j-1] && (S[i] == S[j])。
随后考虑边界条件,所有长度为1的字符串都是回文串,所有长度为2的字符串两个字符需要相同才是回文串。
string longestPalindrome(string s) {
int len = s.length(), maxlen = 1;
string maxstr = "";
maxstr += s[0];
vector<vector<bool> > p(len, vector<bool>(len));
for(int i = 0; i < len; i ++) p[i][i] = true; //长度为1必然回文
for(int l = 2; l <= len; l ++) { // 子串长度
for(int i = 0; i < len; i ++) { // 起始位置
int j = i + l - 1;
if(j >= len) break;
if(l == 2) p[i][j] = (s[i] == s[j]); // 需要特判长度2的子串,否则i+1>j-1
else p[i][j] = (p[i + 1][j - 1] && (s[i] == s[j]));
if(p[i][j] && l > maxlen) {
maxlen = j - i + 1;
maxstr = s.substr(i, maxlen);
}
}
}
return maxstr;
}
中心扩展法
长度为1的字符串必然为回文串,以一个字符为中心,可以向两边扩展。
这里的扩展有两种情况:
第一种为\(aba\)格式,以\(b\)作为字符串中心,从左右邻居开始扩展;
第二种是\(abba\),从自身开始,和右边的邻居一起扩展。
string longestPalindrome(string s) {
string res = "";
for(int i = 0; i < s.length(); i ++) {
int l = i - 1, r = i + 1;
while(l >= 0 && r < s.length() && s[l] == s[r]) l --, r ++;
l ++, r --; // 还原边界
if(res.size() < r - l + 1) res = s.substr(l, r - l + 1);
l = i, r = i + 1;
while(l >= 0 && r < s.length() && s[l] == s[r]) l --, r ++;
l ++, r --;
if(res.size() < r - l + 1) res = s.substr(l, r - l + 1);
}
return res;
}
Manacher算法
预处理
回文串长度为奇数,则其对称位置在某个字符。否则在两个字符中间,非常不利于计算回文串长度。
处理方法:在字符串两边加\(\#\),任意两个字符串之间加\(\#\)。最后在开头和结尾加两个不同的字符\(\$\)和^,破坏循环条件。
那么处理后的字符串长度 = 原长度 * 2 + 1。这样的处理保证了任意字符串都是奇数字符串。如果知道字符串半径就可以求出字符串长度,也就可以求出原字符串长度。原字符串长度 = (字符串长度 - 1)/ 2 = (r * 2 - 1 - 1) / 2 = r - 1。(假设该字符串就是回文串,因此字符串长度 = r * 2 - 1,因此规定一个字符的回文串半径为 1)
关于 字符串长度 = r * 2 - 1 有如下示意。
r : 0 1 2 1 4 1 2 1 0
$#0#1#2#1#4#1#2#1#0#^
算法过程
维护一个最靠右边的回文串(\(S[l,r]\)),计算一个记录着以当前字符 $s[i] $为中心的回文串的最大半径 \(ans[i]\)。每次计算有以下情形:
- 更新 \(ans[i]\) 时可以利用对称性
- \(ans[i]\) 关于 最右边的回文串的对称字符串在 (\(S[l,r]\)) 范围内,那么 \(ans[i] = ans[j]\) (\(j\) 为对称子串的中心),可以知道\(i + j = 2 \times mid\)
- 不在范围内,因为(\(S[l,r]\)) 是最右的回文串,所以 \(ans[i]\) 等于其对称子串在 \(S[l,r]\) 中的最大半径。(因为其对称子串范围超过了 \(S[l,r]\),且 \(S[l,r]\) 无法向右扩张,即$ str[sr + 1] != str[sl - 1]$。 那么此时 \(ans[i]\) 就等于其对称子串在\(S[l,r]\)范围内的半径)
- 不可以利用对称性就,先置最大半径为1,暴力向外扩张求 \(ans[i]\),即左右边界对比相等就半径加一继续对比即可。
计算结束后,用本次 \(ans[i]\) 更新 最靠右的回文子串。
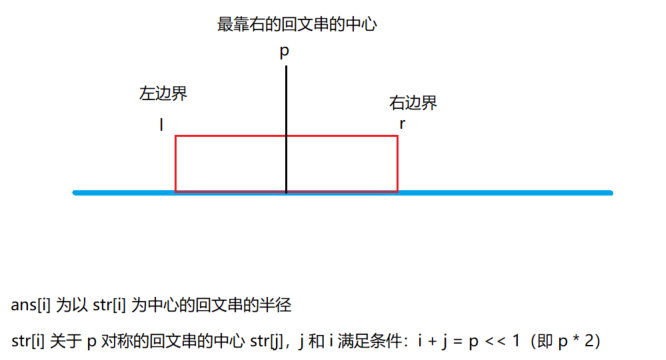
什么情况下可以利用我们维护的最靠右的回文串的对称性?
我们是一边顺序求解$ ans[i]$,一边维护一个最靠右的回文串,所以我们求解的 \(i\),只可能在 \(p\) 的右边,即 \(i \leq p\)。只要我们求解的 \(i\),还在这个维护的回文串的范围内,即\(l \leq i \leq r\),就可以利用其对称性。因为这个回文串是最靠右的最大的回文串,意味着他不能向外扩张,而且我们的 \(i \leq p\)。所以,我们只要看在这个最右回文串中以 \(str[j]\)为中心的回文串即可(即 \(str[j]\) 在最右回文串中关于 p 的对称回文串)。但是以 \(str[j]\) 为中心的回文串,可能很长超过了 \([l,r]\) 的范围,也可能其长度就在这个范围内,因此就可能有两种情况。
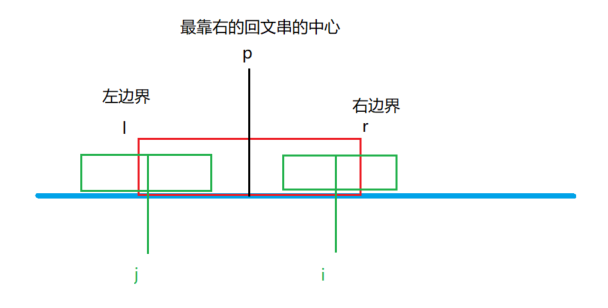
可能的两种情况分别怎么求?
对称串的长度在范围内,那么就很简单,之前已经求过了,而且最右回文串已经是最靠右的了,不能在中心不变的情况下向外扩展,因此 \(ans[i] = ans[j](j = p << 1 - i)\)。不在范围内,意味着\(str[j]\)为中心的回文串长度超过了最右串的范围,因为最右串不能扩展,即 \(str[l - 1] != str[r + 1]\),因此我们可以推到出 \(ans[i]\) 不能等于 \(ans[j]\),否则就会导致我们求的不是最靠右的回文串,这就矛盾了。这里可以据图假设反推。\(ans[i]\) 只能取一个小一点的值,这个值就是以 \(str[j]\) 为中心的回文串,在 \([l,r]\)范围内的半径。这里等于 \(j - l\) 等价于 \(r - i\)。
int p[2010];
void manacher(string b)
{
int mr = 0, mid;
for (int i = 1; i < (int)b.length(); i ++)
{
if (i < mr) p[i] = min(p[mid * 2 - i], mr - i);
else p[i] = 1;
while (b[i - p[i]] == b[i + p[i]]) p[i] ++; // 暴力递增
if(i + p[i] > mr) // 扩展右边界
{
mr = i + p[i];
mid = i;
}
}
}
string longestPalindrome(string s) {
string b;
b += "$#";
for(int i = 0; i < (int)s.length(); i ++) b += s[i], b += "#";
b += "^";
manacher(b);
int res = 0, pos = 0;
for(int i = 0; i < (int)b.length(); i ++){
if(p[i] > res){
res = p[i];
pos = i;
}
}
string str = b.substr(pos - res + 1, res * 2 - 1);
string ans = "";
for(int i = 1; i < str.length(); i += 2) ans += str[i];
return ans;
}


