语法入门
牛客竞赛语法入门班
程序设计入门
-
#include <bits/stdc++.h> //#define LOCAL using namespace std; typedef long long ll; #define IOS ios::sync_with_stdio(false); cin.tie(0); cout.tie(0); const double pi=acos(-1.0); const int INF=1000000000; const int maxn=1000005; int main() { IOS; #ifdef LOCAL freopen("input.txt","r",stdin); freopen("output.txt","w",stdout); #endif return 0; } -
#define IOS ios::sync_with_stdio(false); cin.tie(0); cout.tie(0); IOS; //加速cin和cout //这种情况下cin和scanf就不能混用了 //缩减时间复杂度 当要判断string=="add"还是"del"还是"query" 我们可以直接判断s[0]='a'还是'd'还是'q' 也能加速 -
return 0;表示主函数需要返回一个0,这说明程序正常运行结束。在主程序中即使不写这一句话,编译器也会在编译的时候自动加上这句话。千万不要return一个非0的数,这会被认为是运行错误。
-
万能头 #include <bits/stdc++.h>
-
当题目里面没说数据范围,整数用long long
-
整数除法与实数除法 除与模
-
整数与小数的二进制表示
不循环小数被转为二进制后会成为循环小数,再计算机存储时会截断循环小数,所以会造成误差,当两个小数的差小于10的某次方时,默认为两个小数相等。
十进制小数转二进制 乘以2并取整
-
原码 0正1负
反码 正数的反码等于本身 负数的反码等于绝对值的原码各位取反(包括符号位)
补码 正数的补码等于本身 负数的补码等于反码+1
正负数的加减可以转换为各自的补码在进行加的运算
-
常变量 const int N 310;
-
无符号类型可以扩展有符号类型变量最大能表达的值
eg.int -2147483648~+2147483647 unsigned int 0~2147483848+2147483647
一般来说用int和double int存储不了就用long long
-
每行输出都应该以回车符结束,包括最后一行
-
整数类型:
| short | int | long | long long |
|---|
- 实数类型
| float | double | long double |
|---|
- 字符类型 char
- 逻辑类型 bool
顺序结构程序设计
-
定义变量时,若定义在main函数里面,则为未知数,若定义在main函数之外,则为0
-
八进制022 (%o),十六进制0x12(%x)
-
常量整数默认为int类型,可以转换成longlong类型,即22LL
-
c++中保留数字精度
#include <iomanip>保留6位有效数字 Cout<<setprecision(6)<<a;
保留6位小数(与fixed连用) Cout<<fixed<<setprecision(6)<<a;
-
将小写字母转换为大写字母 输入x 判断第几个小写字母 x-'a'+'A'
-
数学函数
#include <cmath>Sin() cos() tan() asin() acos() atan()
Pow() sqrt() log() log10()
Ceil() floor() fabs()
-
c++中c风格的输入输出
#include <cstdio>Long long %lld
printf输出时默认保留6位小数
cout输出时默认保留6位有效数字
%m.nd m为最小显示宽度 n为小数位数
%-md -表示左对齐 +表示正数带上正号
在没有说明数据范围的情况下,整数尽量开long long
%02d 当整数不是两位数时用0去填充十位

-
输入三位数的时候可以scanf("%1d%1d%1d",&a,&b,&c); 从而得到三位数每一位的数字
在输出时间时可以直接用scanf("%4d:%4d:%4d",&h1,&m1,&s1);
-
算法库函数
#include <algorithm>Min(a,b)
Max(a,b)
swap(a,b)
多个数进行比较:max({a,b,c,d});
fabs输出的是double类型 (c需要用%f,除非强转为int,c++直接cout
-
double输入是lf,输出是f 整数值用%d输出,实数用%f输出
选择结构程序设计
-
可以多用三目运算符 ? :
-
浮点数相等不能用==比较,fabs(a-b)<1e-6 来判断浮点数是否相等
-
关系运算符: > < >= <= == !=
关系运算符的真假可以当成数值使用
-
记不得运算符优先顺序就加括号
-
与&& 或|| 非!
(a)&&(b) 当判断a为假时就不会去执行b
(a)||(b) 当判断a为真时就不会去执行b
-
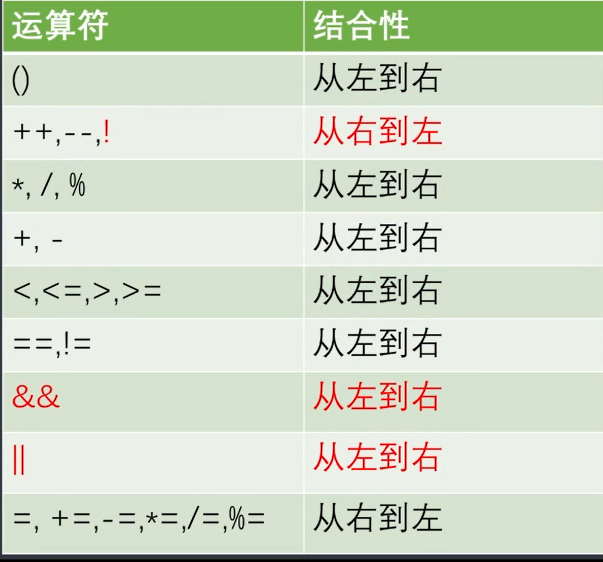
运算符优先级
-
c++里面记得用bool
-
小数据可以用cin、cout,大数据一定要用scanf、printf
-
尽量用‘\n’来替代endl
-
example: int b= (a>85) + (b>75) +(c>90) ; 就可以用(c>90)来做判断条件并输出其真假
-
闰年:年份为4的倍数但不是100的倍数 , 或为400的倍数
-
if - else: else if 与if+if相比能降低复杂度
-
switch-case
switch () { case 1: break; ...... default: }switch后面()内的值必须为整数数值
循环结构程序设计
-
逗号表达式 , 执行逗号前后的表达式,但以逗号后面的表达式的值作为结果
-
for (int i=1;i<=n;ans+=i,i++); //等价于 for (int i=1;i<=n;i++) { ans+=i; } -
break continue
-
*scanf有值 当读入几个变量,值就为几 当没有读入时,scanf的值为EOF,即-1
cin只要少读或者不读就是no e.g. cin>>a>>b; 最后输入的时候,假如直接ctrl+z结束或者只读了一个数,返回值就是false
while (~(scanf("%d",&n))) //成功读到了数据数量,不匹配0,失败EOF(-1) while (cin>>a) //成功读完了为true,不匹配或失败为false统计字符个数时, 能够读进空格,tab,换行符 scanf(" %c",&m); 用空格忽略空白符
-
当读入字符时 cin>>a 可以直接读入字符,不会读入tab和回车 但是scanf会读入,因此使用scanf(" %c",a) %前面的空格会抵消tab和回车
-
在main函数外面定义数组、变量,定义在using namespace std; 下面
-
产生随机数:
#include <iostream> #include <cstdlib> #include <ctime> using namespace std; srand(time(0)); ans = rand()%100+1; //%a 生成0到a-1的随机数 -
#include <time.h> printf("Time used=%.2f\n",(double)clock()/CLOCKS_PER_SEC); //返回程序目前为止运行的时间,除以常数CLOCKS_PER_SEC之后得到的值便是以秒为单位
位运算
-
& | ~ ^ >> <<
-
& 按位与运算 两位都是1才为1
- | 按位或运算 两位有一位为1就是1
- 按位取反运算
^ 按位异或运算 判断两个值是不是不一样 不一样为1 一样为0 可以看成不进位的加法
-
拿二进制数最后一位的思路: a&1 (a&000001=) a>>1
-
1000瓶液体,有一瓶为毒药,喂给小白鼠一滴会在一小时内死掉,只有一小时时间,问最少需要几只小白鼠?
1~1000化为二进制 0000000001~1111101000 喂给第一只小白鼠尾号为1的液体,假如第一只小白鼠死了,则毒药编号的尾数为1
以此类推,第二只小白鼠喂给倒数第二位为1的液体,若死去,则毒药编号的倒数第二位为1
- 扩展,假如给了两个小时,该如何设计实验?
- a*2=a<<1
数组
-
数组元素在内存中是连续储存的
-
给数组赋值的时候 给第一个元素赋值为0,其余的会自动补充为0
-
开数组的时候开大一点,多开10个 尽量不要在开数组时出现未知数
-
for 里面写++i 运行会更快一些
-
有若干个排列在一条直线上的点pi,每个点上有ai个人,找出一个人使得所有人移动到这个人的位置上的总距离最小
假设已经求出所有人到第一个点的距离, 然后对于下一个点,有第一个点的人数要多走差值的步数,>1的点的人数会少走差值的步数
count[i]来存储i点之前的总人数
dist'=dist + count[i] * (x,y) - (sum-count[i]) * (x,y)
- 对于一个循环数组 向后加 就是(x+i)%n 向前减 就是 ((x+i)+n)%n
带权中位数
-
带权中位数,就是给定的N个数都有一个权值。此时的中位数就不再是第N/2个数了,而是第∑DI/2个数。
带权中位数问题: 给出了若干个排列在一条直线上的点,每个点有一个权值,比如说货物量、人数什么的,然后让我们找出使所有点的货物、人集合到一个点的总代价最小的位置。我们将会发现,这一类问题实际上就是带权中位数问题。
十进制转二进制
#include <iostream>
using namespace std;
int a[20];
int main()
{
int x;
cin>>x;
int i=0;
while(x){
if (x&1) a[i]=1;
x>>=1; i++;
}
for (int j=i-1;j>=0;j--) cout<<a[j];
return 0;
}
排序
计数排序
对于数据较小的情况,直接开一个n的数组,读到哪个数就把数组加一,只能用于排序值域不是很大的数字,基于分类的排序
(只需要开一个大小不小于n的数组作为票箱,依次读入选票,然后将选票号数加到对应的票箱中,最后按照每个票箱的数量依次输出候选人编号即可。在这个过程中,甚至不需要存储每一张选票)
读入选票并统计的时间复杂度为O(n),输出选票的时间复杂度为O(n+m)
选择排序
从第一张牌到最后一张牌中找到最小的一张,放在最前面,然后从第二张牌到最后一张牌中继续寻找最小的一张牌,放到第二位
第一次:扫描整个数组,将最小的数放到第一个位置(将原来在第一个位置 的数与最小的数做交换)
算法复杂度O(n2)
int a[10010],n;
void Selection_Sort(int a[]){
for(int i=0;i<n-1;i++){
for(int j=i+1;j<n;j++){
if(a[j]<a[i]){
swap(a[j],a[i]);
}
}
}
}
#include <algorithm>
swap (a,b)
//交换a和b的值
//扫一遍数组得到最小值,并与首个进行交换,最后一个自然是最大的,所以只要进行n-1次循环
for (int i=0;i<N-1;i++){
int pos = i;
for (int j=i ; j<N;j++){
//首先默认第i个位置为最小值,并从此往后开始寻找最小值并交换
if (a[j]<a[pos]) pos=j;
}
swap (a[i],a[pos]);
}
冒泡排序
每次比较相邻的两个数,调换他们的位置,一次之后最大的数便浮在了最上面
int a[10010],n;
void Bubble_Sort(int a[]){
for(int i=0;i<n-1;i++){
for(int j=0;j<n-i-1;j++){
if(a[j]>a[j+1]) swap(a[j],a[j+1]);
}
}
}
时间复杂度O(n2)
//冒泡排序 每次交换相邻的两个数,一共进行n-1次
//升序的话 将最大的放到最上面,
for (int i=0;i<N-1;i++){
for (int j=0 ; j<N-1-i;j++){
if (a[j]>a[j+1]) swap(a[j],a[j+1]);
}
}
插入排序
扑克牌,懂?
int a[10010],n;
void Insertion_Sort(int a[]){
for(int i=1;i<n;i++){
int now=a[i],j;
for(j=i-1;j>=0;j--)
if(a[j]>now) a[j+1]=a[j];
else break;
a[j+1]=now;
}
}
通过构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入。
//插入排序 第一个为有序,从第二个开始直到末尾进行插入
//对于每个待排序元素,依次和前面的进行比较,假如小就交换位置,假如大或一样就去排下一个
for (int i=1;i<N;i++){
int key =a[i];
int j=i-1;
while (j>=0 &&a[j]>key){ //while循环有时候可以取代for循环
a[j+1]=a[j];
j--;
}
a[j+1]=key; //此处一定要记得加一
}
希尔排序
递减增量排序算法 不稳定
先将整个待排序的记录序列分割成为若干子序列分别进行直接插入排序,待整个序列中的记录"基本有序"时,再对全体记录进行依次直接插入排序。
第一次以n/2作为步长,然后每次再除以2作为步长,对于每个步长依次进行插入排序,从而形成一个相对有序的序列,最后再对整体进行步长为1的插入排序
int i,j,inc,key;
//采用初始增量n/2 , 每一趟之后都再次除以2
for (inc=N/2; inc>0 ; inc/=2){
//对于每一趟都采用插入排序
for (i=inc ; i<N;i++){
//第一个必然是有序的所以从第二个步长开始排序
key=a[i];
for (j=i ; j>=inc&&key<a[j-inc];j-=inc){
a[j]=a[j-inc];
}
a[j]=key;
}
}
快速排序
对于一个无序数列,找到一个哨兵数,将序列中所有比哨兵数小的数字都在哨兵数的左边,所有比哨兵数大的数字都在哨兵数的右边,然后对哨兵数左边和右边在使用同样的方法找到新的哨兵数,并再次进行分类,直到集合不可再分为止
怎么寻找哨兵呢?随便选
算法复杂度O(nlog n)
int a[10010],n;
void Quick_Sort(int a[],int l,int r){
int i=l,j=r,flag=a[(l+r)/2];
do{
while(a[i]<flag) i++;
while(a[j]>flag) j--;
if(i<=j){
swap(a[i],a[j]);
i++;
j--;
}
}while(i<=j);
if(l<j) Quick_Sort(a,l,j);
if(i<r) Quick_Sort(a,i,r);
}
Quick_Sort(a,0,n-1);
二路归并排序
sort
O(nlogn)
#include <algorithm>
sort(a,a+n,cmp)
//first_pointer:数组首地址,(数组名) 数组名+数组元素个数
//默认升序,cmp此时可忽略
//假如要用其他排序规则,需要自定义cmp
bool compare(int a,int b){
return a<b; //升序排列,如果改为return a>b,则为降序
}
//对结构体
struct shi{
int h;
int m;
int s;
int sum;
};
bool compare(struct shi a,struct shi b){
return a.sum<b.sum;
}
struct shi a[5010];
sort(a,a+n,compare);
unique(去重)
unique(a,a+n)
//对a数组从a[0]到a[n-]进行 去重,要求a数组已经有序,返回去重后最后一个元素对应的指针(理解他减去的指针得到的值就是去重后得到的元素个数
sort(a,a+n);
cnt=unique(a,a+n)-a;
for(int i=0;i<cnt;i++) cout<<a[i]<<" ";
nth_element(寻找第k小的数字)
nth_element,这个函数主要用来将数组元素中第k小的整数排出来并在数组中就位,随时调用,可谓十分实用。
nth_element(数组名,数组名+第k小元素,数组名+元素个数)
#include <bits/stdc++.h>
using namespace std;
int a[5000010];
int main(){
int n,k;
cin>>n>>k;
for(int i=0;i<n;i++) scanf("%d",&a[i]);
nth_element(a,a+k,a+n);
printf("%d",a[k]);
return 0;
}
//输出第k小的数字
或者采用分治,即快速排序的改版
字符串与结构体
-
0 ——48 A——65 a——97
-
字符数组 char a[100];
scanf("%s",a); cin>>a; a==&a[0] 字符数组的地址就是字符数组第一个元素所在的地址 数组名本身就是字符数组的地址, 不需要用&
字符数组在内存中以 ‘\0’ 字符结尾
假如想从字符数组的第二个位置即a[1]开始存储,可以 scanf("%s",a+1);
-
只有放在main外面,数组a才可以开得很大,放在main里面的话,数组稍大就会异常退出。
-
字典序,即为字符串在字典中的顺序。对于两个字符串,从第一个字符开始比较,当某一个位置的字符不同时,该位置字符较小的串,字典序较小;如果其中一个字符串已经没有更多字符,但另一个字符串还没结束,则较短的字符串的字典序较小。
-
字符串的子串是连续的字符串,但是子序列是维持原有顺序的,挑选出来的元素组成的字符串,不一定是连续的
-
从数组a复制k个元素到数组b,可以
#include <s memcpy(b,a,sizeof(int)*k)如果要把数组a全部复制到数组b中,可以
memcpy(b,a,sizeof(a)); -
#include <bits/stdc++.h> using namespace std; int main(){ char s; while(1){ s=getchar(); if(s==EOF) break; if('a'<=s&&s<='z') s+='A'-'a'; putchar(s); } return 0; }运行程序,结果发现无论输入什么,程序都没有反应,因为程序不认为输入已经结束了,继续在等待输入
所以在输入完字符串后,按一下ctrl+Z ,再按一下回车,就可以完成读入了
程序中读入一个字符都会判断是否读完了整个文件,如果文件被读完了,getchar就会返回EOF,标志已经读入结束
c++11已经删除了gets()函数,因为存在字符数组越界的风险
但是puts()还可以使用,同时会自动输出换行
-
求字符串长度
#include <cstring> int lenth = strlen(s); while (str1[i]!='\0'){ length++; i++; } -
查询字母在字符串中的位置
#include <cstring> int pos = strchr (s,'c') - s; // strchr返回的是指向'c'的指针 想要获得位置就必须减去头指针 -
将字符串s2复制到s1中,(覆盖)
#include <cstring> strcpy(s1,s2); -
将字符串s2拼接到s1尾部
#include <cstring> strcat (s1,s2); -
按字典序比较字符串大小
#include <cstring> strcmp (s1,s2); //s1>s2 返回1 s1<s2 返回-1 s1==s2 返回0 -
在字符串中寻找字符串
#include <cstring> if (strstr(s1,s2)==NULL) printf("no found"); else int pos = strstr (s1,s2) - s1; //在s1中寻找s2 -
string类 (stl库)
不要随便瞎打getchar。。。。第一行输入数字第二行输入就直接俩cin,别作死
#include <string> string s1,s2; cin>>s1>>s2; //只能用cin,cout输入输出 //cin输入会忽略前面的空格,所以我们可以while(cin>>s)进行多次输入 getline(cin,s1); //读一行 s1+=s2; //将s2接到s1后面 s1.append(s2) //将s2接到s1后面 s1 == s2 s1 <= s2 //比较字符串大小 len = s1.length(); //求字符串长度 s1.substr(pos,len) //截取子串长度,从pos开始截取长度为len的子串 s1.insert(pos,s2) //插入子串 s1.find(str,[pos]) //查找子串str,pos代表可有可无,从pos位开始查找 ,返回位置 //使用find函数查找子串但是找不到的时候会返回string::npos,但是由于不一定是int类型的常量,所以需要强制转换为int类型才能输出-1 cout<<(s1.find(s2,5)==string::npos); //找到了返回0,未找到返回1 find_first_not_of(str,num) //从字符串第num+1个字符开始查找第一个与str中的字符都不匹配的字符,返回它的位置。搜索从num 开始。如果没找到就返回string::nops str.erase(iter1,iter2) //删除[iter1,iter2)包含的字符 //比如要删掉字符串开头的前导0就可以 s2.erase(0,s2.find_first_not_of('0')); //string中提供的成员函数可以用来删除字符串中的字符,这里主要介绍erase方法 basic_string & erase(size_type pos=0, size_type n=npos); //即从给定起始位置pos处开始删除, 要删除字符的长度为n, 返回值修改后的string对象引用 string str = "hello c++! +++"; // 从位置pos=10处开始删除,直到结尾 // 即: " +++" str.erase(10); cout << '-' << str << '-' << endl; // 从位置pos=6处开始,删除4个字符 // 即: "c++!" str.erase(6, 4); cout << '-' << str << '-' << endl; //fgets()函数来进行读入一行字符串,并存入字符数组中,空格也一起存下了 char s[20]; fgets(s,sizeof(s),stdin); //语句中指定了字符数组的最大读入数 //sscanf()函数可以从已经存储下来的字符串中读入信息,sprintf可以将信息输出到字符串中 sscanf(s,"%d",&a); //从s字符串中读入一个整数a,scanf是从标准输入中读入,sscanf从给定的一个字符串中读入,所以要求提供字符数组的名称,表示从哪儿字符串里面输入信息 sprintf(s,"%d",a); //将一个int类型的数a输出到字符串s中而不是标准输出。反转字符串
#include <algorithm> string N; reverse(N.begin(),N.end());碰到字符串中有空格的情况,只能用getline进行输入
也许字符串的操作速度比字符数组快
仍然可以用数组的形式去访问字符串的元素
string的表示为 "." 是双引号 单个字符才为单引号
-
结构体
typedef struct{ 成员列表; }别名; -
memset
#include <cstring> int prime[100]; memset (prime, 0 ,sizeof(prime));memset也可以对二维数组使用,头文件一定要加cstring
**理论上说,memset里面只能赋值为 0 , -1 , 0x3f , 0x7f **
0x7f表示很大的数 , 假如要进行相加操作,容易溢出,使用0x3f会比较合适
一般来说,可以 min=0x7f , max=0xf7
数字与字符串转换
数字to字符串
//方法一(利用<sstream>的stringstream,可以是浮点数)
#include <iostream>
#include <sstream>
using namespace std;
int main()
{
double x;
string str;
stringstream ss;
cin >> x;
ss << x;
ss >> str;
cout << str;
return 0;
}
//sstream相当于int和string的中介
//方法二(利用<sstream>中的to_string()方法,浮点数会附带小数点后六位,不足补零,不推荐浮点数使用)
#include <iostream>
#include <sstream>
using namespace std;
int main()
{
double x;
string str;
cin >> x;
str = to_string(x);
cout << str;
return 0;
}
字符串to数字
//方法一(利用<sstream>的stringstream,可以是浮点数) **通用**
#include <iostream>
#include <sstream>
using namespace std;
int main()
{
double x;
string str;
stringstream ss;
cin >> str;
ss << str;
ss >> x;
cout << x;
return 0;
}
//方法二(利用<string>中的stoi()函数,其中还有对于其他类型的函数,如stod(),stof()等,根据类型选取)
#include <iostream>
#include <string>
using namespace std;
int main()
{
int x;
string str;
cin >> str;
x = stoi(str);
cout << x;
return 0;
}
//atol() 函数是 cstdlib 头文件的库函数。它用于将给定的字符串值转换为整数值。它接受一个包含整数(整数)数的字符串并返回其长整数值。
//看不明白,算了,法一也可以用于long long的转换
不区分大小写进行字符串比较
方法一:(tolower/toupper)实现字母的大小写转换
#include <cctype>
//tolower从大写到小写
//tolower是单个字符的大小写转换,要实现字符串可以循环
string str;
getline(cin,str);
for (int i=0; i <str.size(); i++)
str[i] = tolower(str[i]);
cout<<str<<endl;
//toupper从小写到大写
string str;
getline(cin,str);
for (int i=0; i <str.size(); i++)
str[i] = toupper(str[i]);
cout<<str;
//头文件是cctype
方法二:tolower/toupper+迭代器
#include <algorithm>
#include <cctype>
//toupper小写转大写
string s;
getline(cin,s);
transform(s.begin(),s.end(),s.begin(),::toupper);
//tolower大写转小写
string s;
getline(cin,s);
transform(s.begin(),s.end(),s.begin(),::tolower);
文件操作与重定向
#include <cstdio>
//将输入输出方式重定向到文件输入输出中
freopen("title.in","r",stdin);
freopen("title.out","w",stdout);
//在online judge中,编译会定义宏,检测到宏就不会进行重定向
#ifndef ONLINE_JUDGE
freopen("title.in","r",stdin);
freopen("title.out","w",stdout);
#endif
函数与递归
-
十进制转二进制 函数
#include <iostream> #include <cmath> using namespace std; unsigned long long ts(int a){ unsigned long long i = 0; unsigned long long sum = 0; while (a>0){ sum += (a%2)*pow(10,i); i++; a /= 2; } return sum; } //不开unsigned long long这里就过不去 int main(){ int a; cin>>a; cout<<ts(a); return 0; } -
一般的函数参数是形参,即只能传值,外面的参数实际值不会改变,但是可以采用int main (int &x , int y)的方式传地址的值进去从而在里面改变外面的参数
void swap(int &x,int &y){ int t=x; x=y; y=t; } //传数组 i -
对于数组 int func(int b[])
-
a = x ? m : n ; 三目运算符
-
阶乘
int jiecheng(int x){ if (x==0) return 1; else return x*dj(x-1); } -
斐波那契数列
int fib(int x){ return (x<=1) ? 1 : fib(x-1) + fib(x-2); } -
汉诺塔
#include <iostream> #include <cstdio> using namespace std; void Hanoi(int n,char a,char b,char c){ //把n个经由b从a移到c if (n==0) return ; Hanoi(n-1,a,c,b); //把n-1个经由c从a移到b printf("move NO.%d from %c to %c\n",n,a,b); //把第n个直接从a移到c Hanoi(n-1,b,a,c); //把n-1个经由a从b移到c } int main(){ int n; cin>>n; char A,B,C; scanf(" %c %c %c",&A,&B,&C); Hanoi(n,A,B,C); return 0; }我的理解:在不会做的时候默认我会做,然后调用。包含递归基础
-
组合数Cnm
long long C(int n,int m) { if(m<n-m) m=n-m; long long ans=1; for(int i=m+1;i<=n;i++) ans*=i; for(int i=1;i<=n-m;i++) ans/=i; return ans; }
树
一种数据结构,由n个有限结点组成的有层次关系的集合。像倒挂的树,根朝上,叶朝下
- 每个节点有0或多个子节点
- 没有父节点的节点称作根节点每一个非根节点有且只有一个父节点
- 除了叶子节点,每个子节点可以分成多个不相交的子树
- 在一般树里,子节点没有大小先后顺序
二叉树
每个节点最多含有两个子树的树称为二叉树,通常分支被称作左子树和右子树
左孩子和右孩子不一样, 尽管看起来可以互换位置,但是其实不一样
二叉树第i层最多拥有 2 ^ (i - 1) 个节点,深度为k的二叉树最多共有2 ^ (k + 1) - 1个节点。
满二叉树
除了最后一层没有任何子节点外,每一层上的所有节点都有两个子节点的二叉树(除了最后一层,每个点往下都有两个分叉)
假设某个二叉树深度为 k,第 i 层拥有 2 ^ (i - 1) 个节点,且总共拥有 2 ^ (k + 1) - 1个节点.
完全二叉树
除了最后一层,每一层的节点数都达到了最大值,并且最后一层只缺少右边的节点(不可能缺少左边的或者中间的节点)
若设二叉树的深度为h,除第 h 层外,其它各层 (1~h-1) 的结点数都达到最大个数,第 h层所有的结点都连续集中在最左边。
先序遍历
先访问根节点,然后遍历左子树,最后遍历右子树。如果二叉树为空就返回。 根左右
中序遍历
先遍历左子树,然后访问根节点,最后遍历右子树。 左根右
在只有右子树的情况下,要先访问根节点,再访问右子树
后序遍历
先遍历左子树,然后遍历右子树,最后访问根节点。 左右根
层序遍历
从左到右,从上到下
-
给出二叉树的前序中序求后序
e.g. 前序遍历 ABCDFE 中序遍历 BADFCE
在前序里面第一个必然是根 然后将这个根在中序里面找出来,那么左边为左子树,右边为右子树
在此题中,A为根节点 中序中得出 B为左子树 DFCE为右子树 前序 CDFE 中序 DFCE
C为根节点 DF为左子树 E为右子树 前序DF 中序DF
D为根节点 F为右孩子
BFDECA
#include <iostream> #include <cstdio> using namespace std; string qian,zhong; void deal(int l1,int r1,int l2,int r2){ if (l1>r1) return ; if (l1==r1){ cout<<qian[l1]; return ; } int pos=0; for (int i=l2;i<=r2;i++){ if (zhong[i]==qian[l1]){ pos=i; break; } } deal(l1+1,l1+pos-l2,l2,pos-1); deal(l1+pos-l2+1,r1,pos+1,r2); cout<<qian[l1]; } int main(void){ cin>>qian>>zhong; int len = zhong.length(); deal(0,len-1,0,len-1); return 0; } -
给出二叉树的中序后序求前序
可求
#include <iostream> #include <cstdio> using namespace std; string zhong,hou; void deal(int l1,int r1,int l2,int r2){ if (l1>r1) return ; if (l1==r1){ cout<<zhong[l1]; return ; } int pos=0; for (int i=l1;i<=r1;i++){ if (zhong[i]==hou[r2]){ pos=i; break; } } cout<<hou[r2]; deal(l1,pos-1,l2,l2+pos-1-l1); deal(pos+1,r1,l2+pos-l1,r2-1); } int main(){ cin>>zhong>>hou; int len = zhong.length(); deal(0,len-1,0,len-1); return 0; } -
给出二叉树的前序后序求中序
求不出来
栈
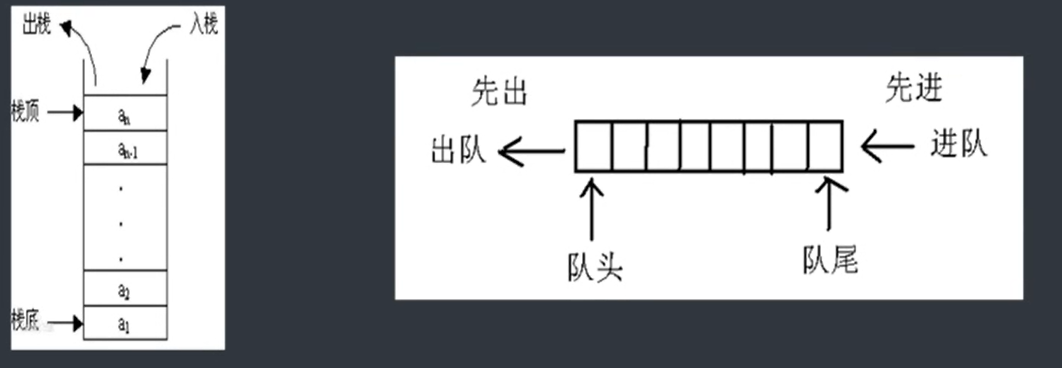
栈:仅在表头进行插入和删除操作的线性表(先进后出,后进先出)
从上往下,栈底封死,要拿出最下面的东西,就必须把最上面的都拿走,所以先进去的反而是后出来的
#include <stack>
stack<int> s; //建立一个栈,内部元素类型为int
s.push(a); //将元素a压入栈
s.pop(); //将栈顶元素弹出
s.top(); //查询栈顶元素
s.size(); //查询s的元素个数
s.empty(); //查询s是否为空
stack常用函数:
push() 向栈顶压入元素
pop() 弹出栈顶元素
top() 访问栈顶元素
empty() 判断是否为空
size() 访问个数
有1、2、3......n个人进栈,判断出栈顺序是否正确
判断栈顶元素和出栈顺序的首元素是否一样,若一样则出栈,若不一样则向栈顶压入元素,重复进行判断
#include <iostream>
#include <cstdio>
#include <stack>
using namespace std;
int a[100];
stack<int> st;
int main(void){
int n,flag=1,k=1;
cin>>n;
for(int i=1;i<=n;i++) scanf("%d",&a[i]);
for (int i=1;i<=n;i++){
st.push(i);
while(!st.empty()&&st.top()==a[k]){
st.pop();
k++;
}
}
while(st.empty()==0){
if (st.top()==a[k]){
st.pop();
k++;
}else if(st.top()!=a[k]){
flag=0;
break;
}
}
if (flag==1) cout<<"YES";
else cout<<"NO";
return 0;
}
队列
队列:特殊的线性表,只允许在表的前端(front)进行删除操作(队头),在表的后端(rear)进行插入操作(队尾),先进先出
#include <queue>
queue<int> q; //建立一个队列q,其内部元素为int
q.push(a); //将元素a插入到队列q的末尾
q.pop(); //删除队列q的队首元素
q.front(); //查询q的队首元素
q.back(); //查询q的队尾元素
q.size(); //查询q的元素个数
q.empty(); //查询q是否为空
queue常用函数
front() 访问队首元素
back() 访问队尾元素
push 向队尾插入元素
pop 弹出队首元素
链表
如果指导每个元素之前之后是谁,就可以恢复整个表的排列顺序
用一个next数组表示每个元素后面的一个元素是什么
分类:
单链表:每个节点记录自己的后继
双链表:每个节点记录自己的前继和后继。与单链表只能往后走相比,双链表可以向前、向后走
循环单链表:本身是一个单链表,但是最后一个结点的后继为第一个节点,从而连接成了环形结构
循环双链表:本身是一个双链表,连成环形
块状链表:
跳表
//排队模拟
struct node{
int pre,nxt; //分别记录前驱和后继结点在数组s中的下标
int key; //节点的值
node(int _key=0,int _pre=0,int _nxt=0){
pre=_pre;
nxt=_nxt;
key=_key;
}
};
node s[1005]; //一个池。以后想要建立一个新的节点,就从s数组里面拿出一个位置给新的节点
int tot=0; //记录s数组目前使用了多少个位置,下一个可用的位置为s
//可以令s[1]恒为起点
int find(int x){ //查找x的节点编号,需要遍历整个链表
int now=1;
while(now&&s[now].key!=x)
now=s[now].nxt;
return now;
}
void ins_back(int x,int y){ //y插在x后面
int now=find(x);
s[++tot]=node(y,now,s[now].nxt); //节点y的前驱为now,后继为s[now].nxt
s[s[now].nxt].pre=tot; //更新原先now的后继的pre值
s[now].nxt=tot; //更新now的后继
}
void ins_front(int x,int y){ //y插在x前面
int now=find(x);
s[++tot]=node(y,s[now].pre,now); //节点y的前驱为s[now].pre,后继为now
s[s[now].pre].nxt=tot; //更新原先now的前驱的nxt值
s[now].pre=tot; //更新now的前驱
}
int ask_back(int x){ //询问x后面的元素
int now=find(x);
return s[s[now].nxt].key;
}
int ask_front(int x){ //询问x前面的元素
int now=find(x);
return s[s[now].pre].key;
}
void del(int x){ //删除元素x
int now=find(x);
int le=s[now].pre;
int rt=s[now].nxt;
s[le].nxt=rt;
s[rt].pre=le;
}
#include <list>
list<int> a; //定义一个int类型的链表a
int arr[5]={1,2,3}; //从数组arr中的前三个元素作为链表a的初始值
list<int> a(arr,arr+3); //从数组arr中的前三个元素作为链表a的初始值
a.size(); //返回链表的结点数量
list<int>::iterator it; //定义一个名为it的迭代器(指针)
a.begin(); //链表开始的迭代器指针
a.end(); //链表末尾的迭代器指针
it++; //迭代器指向前一个元素
it--; //迭代器指向下一个元素
a.push_front(x); //在链表开头插入元素x
a.push_back(x); //在链表末尾插入元素x
a.insert(it,x); //在迭代器it的前面插入x
a.pop_front(); //删除链表开头
a.pop_back(); //删除链表结尾
a.erase(it); //删除迭代器it所在的元素
for(it=a.begin();it!=a.end();it++) //遍历链表
//遍历的时候如果要删除元素,一定要备份出来一个迭代器;否则,it原来指向的节点删除后就不复存在,导致询问下一个节点时会访问无效内存
list<int>::iterator it,now;
it=a.begin();
while(!a.empty()){
cnt++;
now=it;
if(++it==a.end()) it=a.begin();
if(cnt==m){
cout<<*now<<" ";
a.erase(now);
cnt=0;
}
}
//双向链表
#include <list>
list<int> myList;
myList.push_front(1);
myList.push_back(2);
//这两个成员函数分别用于在链表的头部和尾部插入元素。
myList.push_front(x); //在链表开头插入元素x
myList.push_back(x); //在链表末尾插入元素x
typedef list<int>::iterator Iter;
Iter itBegin = myList.begin();
Iter itEnd = myList.end();
for (; itBegin != itEnd; ++itBegin)
printf(" %d", *itBegin);
//这段代码演示的是list提供的,用于访问内部元素的迭代器。迭代器的类型是list<Tp>::iterator
//可以用*运算符访问内部的元素,++和--运算符可以将它后移或前移一位(建议写成前置形式),用==和!=运算符进判断两个迭代器所指的位置是否一致。
//begin()成员函数返回指向头部元素的迭代器。
//end()成员函数返回指向末尾位置的迭代器。这个“末尾位置”指的是最后一个元素再往后一位,也就是说end()所指的位置不包含有效元素,它相当于一个虚设的节点。
//这样设计是为了满足C++标准库表示区间时左闭右开的惯例。
//接上例
Iter it = myList.end();
--it;
//C++11中可以直接写成it = prev(myList.end());
//这里prev是头文件<iterator>提供的函数,用于返回将某个迭代器前移一位的结果
Iter it2 = myList.insert(it, 3);
//myList的内容:1,3,2
//定义了一个迭代器it,然后在end()的基础上左移一位,让它指向链表中最后一个元素。
//insert(it, val)成员函数用于在链表中插入元素。it为该链表的一个迭代器,val为待插入的值,插入后val位于it所指位置的前一位。
//返回值为一个迭代器,表示val插入到了哪个位置。
myList.remove(it);
//myList的内容:1,3
int x = *it + 10; //ERROR!
//remove(it)成员函数用于删除某个迭代器所指的节点。注意在删除之后it就失效了,除非给it重新赋值,否则对它的任何操作都会导致错误!
//size()返回链表内元素的个数
//empty()判断链表是否为空
//remove(val)用于移除所有值为val的节点
//以及作为成员函数的sort()和unique()。(注意sort(myList.begin(), myList.end())是错误的写法)
//unique()删除list中重复的元素
list<int>c0; //空链表
list<int>c1(3); //建一个含三个默认值是0的元素的链表
list<int>c2(5,2); //建一个含五个元素的链表,值都是2
list<int>c4(c2); //建一个c2的copy链表
list<int>c5(c1.begin(),c1.end());
//c5含c1一个区域的元素[_First, _Last)。
//1.assign() 给list赋值 分配值,有两个重载:
c1.assign(++c2.begin(), c2.end()) //c1现在为(50,60)。
c1.assing(7,4) //c1中现在为7个4,c1(4,4,4,4,4,4,4)。
//2.back()返回最后一元素的引用:
int i=c1.back(); //i=30
const int i=c2.back(); //i=60且不可修改
//3.begin()返回第一个元素的指针(iterator)
citer=c1.begin(); // *citer=10
list<int>::const_iterator cciter=c1.begin(); //*cciter=10且为const。
//4.clear()删除所有元素
c1.clear(); //c1为空 c1.size为0;
//5.empty()判断是否链表为空
bool B=c1.empty(); //若c1为空B=true;否则B=false;
//6.end()返回最后一个元素的下一位置的指针(list为空时end()=begin())
citer=c1.end(); //*(--citer)=30;
//同begin()返回一个常指针,不能修改其中元素。
//7.erase()删除一个元素或一个区域的元素(两个重载)
c1.erase(c1.begin()); // c1现为(20,30);
c1.erase(++c1.begin(),c1.end()); // c1现为(10);
//8.front() 返回第一个元素的引用:
int i=c1.front(); //i=10;
const int i=c1.front(); //i=10且不可修改。
//9.insert()在指定位置插入一个或多个元素(三个重载):
c1.insert(++c1.begin(),100); //c1(10,100,20,30)
c1.insert(c1.begin(),2,200); //c1(200,200,20,30);
c1.insert(++c1.begin(),c2.begin(),--c2.end());
//c1(10,40,50,20,30);
//10.max_size()返回链表最大可能长度(size_type就是int型):
list<int>::size_type i=c1.max_size(); //i=1073741823
//11.merge()合并两个链表并使之默认升序(也可改):
c2.merge(c1); //c1现为空;c2现为c2(10,20,30,40,50,60)
c2.merge(c1,greater<int>()); //同上,但c2现为降序
//12.pop_back()删除链表尾的一个元素
c1.pop_back() //c1(10,20);
//13.pop_front()删除链表头的一元素
c1.pop_front() //c1(20,30)
//14.push_back()增加一元素到链表尾
c1.push_back(100) //c1(10,20,30,100)
//15.push_front()增加一元素到链表头
c1.push_front(100) //c1(100,10,20,30)
//16.rbegin()返回链表最后一元素的后向指针(reverse_iterator or const)
list<int>::reverse_iterator riter=c1.rbegin(); //*riter=30
//17.rend()返回链表第一元素的下一位置的后向指针
list<int>::reverse_iterator riter=c1.rend(); // *(--riter)=10
//18.remove()删除链表中匹配值的元素(匹配元素全部删除)
c1.remove(10); //c1(20,30)
//19.remove_if()删除条件满足的元素(会遍历一遍链表)
c1.remove_if( is_odd<int> () ); //c1(10,20,30)
//is_odd自己写(表奇数)
//20.resize()重新定义链表长度(两重载):
c1.resize(4) //c1(10,20,30,0)用默认值填补
c1.resize(4,100) //c1(10,20,30,100)用指定值填补
//21.reverse()反转链表:
c1.reverse(); //c1(30,20,10)
//22.size()返回链表中元素个数
list<int>::size_type i=c1.size(); //i=3
//23.sort()对链表排序,默认升序(可自定义)
c1.sort(); //c1(10,20,30)
c1.sort(great<int>()); //c1(30,20,10)
//24.splice()对两个链表进行结合(三个重载)
//c1.splice(++c1.begin(),c2);
//c1(10,40,50,60,20,30) c2为空 全合并
c1.splice(++c1.begin(),c2,++c2.begin());
//c1(10,50,20,30) ; c2(40,60) 指定元素合并
c1.splice(++c1.begin(),c2,++c2.begin(),c2.end());
//c1(10,50,60,20,30); c2(40) 指定范围合并
//25.swap()交换两个链表(两个重载)
c1.swap(c2); //c1(40,50,60);
swap(c1,c2); //c1(40,50,60)
//26.unique()删除相邻重复元素(断言已经排序,因为它不会删除不相邻的相同元素)
c1.unique();
//假设c1开始(-10,10,10,20,20,-10)则之后为c1(-10,10,20,-10)
c1.unique(mypred); //自定义谓词
STL
算法类
最大值最小值
min max
查找
int p=lower_bound(a,a+n,x)-
快速排序
sort ( a,a+10 ); 相当于左闭右开 a[10]是排不到的
sort (a , a+n , [compare]); compare函数是自定义的比较函数
struct xuesheng{
int ch,ma,en,sum,num;
}a[310];
bool comp(xuesheng a , xuesheng b){
if (a.sum>b.sum) return 1;
if (a.sum == b.sum&&a.ch>b.ch) return 1;
if (a.sum == b.sum&&a.ch==b.ch&&a.num<=.num) return 1;
return 0;
}
sort (a+1,a+300+1,comp);
//或者直接在结构体里面重载运算符
struct xuesheng{
int ch,ma,en,sum,num;
bool operator < (const xuesheng b){
if (sum<b.sum) return 1;
if (sum == b.sum&&ch < b.ch) return 1;
if (sum == b.sum&&ch ==b.ch&&num>b.num) return 1;
return 0;
}
}a[310]
struct ty
{
double x,y,z;
ty operator * (const ty b)
{
ty t;
t.x = y*b.z-b.y*z;
t.y = b.x*z-x*b.z;
t.z = x*b.y-b.x*y;
return t;
}
ty operator +(const ty b)
{
ty t;
t.x= x+b.x;
t.y= y+b.y;
t.z= z+b.z;
return t;
}
ty operator /(const int k)
{
ty t;
t.x = x/k;
t.y = y/k;
t.z = z/k;
return t;
}
}a[10];
数据交换
swap
求下一个排列
include
next_permutation(a,a+n)
e.g. 1,2,3的所有排列方式 123 132 213 231 312 321 用数组存储1 2 3 进行第一次求下一个排列的操作后会变成132
不过这个函数没有输出,而是直接把数组变成了它的下一个字典序。
#include <iostream>
#include <algorithm>
using namespace std;
int a[5]={1,2,3};
int main(){
int k=5;
for(int i=0;i<3;i++) cout<<a[i]<<" ";
cout<<endl;
while(k--){
next_permutation(a,a+3);
for(int i=0;i<3;i++) cout<<a[i]<<" ";
cout<<endl;
}
return 0;
}
//next_permutation的计算次数可以用Cnm来实现
容器类
字符串
string
可变长度数组
vector
不知道数组开多大的时候就开vector
#include <vector>
vector<int> v(N,i)
//建立一个可变长度数组v,内部元素类型为int,该可变数组最开始有N个元素,每个元素初始化为i。可以省略i,也可以省略<N,i>,此时这个数组的长度为0
vector<int> xue;
int a;
cin>>a;
xue.push_back(a);
//将元素a插入数组的末尾,并增加数组长度
xue.size()
//返回数组长度
xue.resize()
//重新调整数组大小为n,如果n比原来的小,则删除多余的信息,如果n比原来大,则新增的部分都初始化为m,其中m可以省略
sort(xue.begin(),xue.end());
//v.begin指向第一个元素,也就是v[0]的指针,end指向最后一个元素的下一个位置,类似于空指针,不指向任何元素
//迭代器
vector<int>::iterator it; //类型::iterator 迭代器名;
//迭代器类似指针,可以认为是一个指向vector的元素的指针。*it可以取出该指针中的元素
for (it=v.begin();it != v.end();it++){
printf("%d %d\n",it->sum,it->num);
}
//初始化二维数组
vector< vector<int> > locker(n+1);
//注意尖括号里面的空格,以免被认为是移位运算符而编译错误
//要存入二维数组的第i行第j个元素,可以用以下形式来拓展
if(locker[i].size()<j+1)
locker[i].resize(j+1);
vector<int> v{3,4,5,1,2,5,3};
//排序
sort(v.begin(), v.end());
//1 2 3 3 4 5 5
//pos是去重以后vector中没有重复元素的下一个位置的迭代器。
vector<int>::iterator pos = unique(v.begin(), v.end());
//去重后整个容器
for (int i = 0; i < v.size(); i++)
{
cout << v[i] << ' ';
}
cout << endl;
//1 2 3 4 5 5 5
//从容器开始到pos:去重后的容器元素
for (vector<int>::iterator i = v.begin(); i < pos; i++)
{
cout << *i << ' ';
}
cout << endl;
//1 2 3 4 5
//从pos到容器结束:无意义的元素
for (vector<int>::iterator i = pos; i < v.end(); i++)
{
cout << *i << ' ';
}
cout << endl;
//5 5
//去重原来是这个意思。。。
//erase()擦除无意义的部分
vector<int> v{3,4,5,1,2,5,3};
sort(v.begin(), v.end());
//1 2 3 3 4 5 5
vector<int>::iterator pos = unique(v.begin(), v.end());
v.erase(pos, v.end());
for (int i = 0; i < v.size(); i++)
{
cout << v[i] << ' ';
}
cout << endl;
//1 2 3 4 5
可以理解为链表,很像链表的顺序容器
原理:先开一个4的数组,不够用就开一个8的数组,把4的数组内的元素转移并销毁4的数组,8不够就开16、32...
-
数据访问功能 operator[] top() back() 还是数组,可以下标访问,top是第一个元素,back是最后一个元素
-
简单的数据操作
删除erase (int index , int size)
插入insert (int index , int size)
添加到数据后面push_back(int value)
弹出最后一个数据pop_back(int value)
-
自身属性操作
数据大小size() 重新整理内存单元resize (int size)
-
整体操作
清空clear() 是否为空 empty()
-
迭代器
访问容器内部数据的指针 返回第一个元素的迭代器begin() 返回容器末尾的迭代器end() 同样遵循左开右闭原则
vector<int> a; vector<int>::iterator it; for (it=a.begin();it!=a.end();it++)
双端队列deque
- deque 容器也擅长在序列尾部添加或删除元素(时间复杂度为
O(1)),而不擅长在序列中间添加或删除元素。 - deque 容器也可以根据需要修改自身的容量和大小。
deque 还擅长在序列头部添加或删除元素,所耗费的时间复杂度也为常数阶O(1)。
当需要向序列两端频繁的添加或删除元素时,应首选 deque 容器。
deque<int> d;
deque<int> d(10);
deque<int> d(10, 5);
//创建一个具有n个元素的deque容器,并为每个元素都指定初始值,如上创建了一个包含10个元素(值都为5)的deque容器。
deque<int> d1(5);
deque<int> d2(d1);
//在已有 deque 容器的情况下,可以通过拷贝该容器创建一个新的 deque 容器
//采用此方式,必须保证新旧容器存储的元素类型一致
d.begin(); //返回指向容器中第一个元素的迭代器
d.end(); //返回指向容器最后一个元素所在位置后一个位置的迭代器
d.rbegin(); //返回指向最后一个元素的迭代器
d.rend(); //返回指向第一个元素所在位置前一个位置的迭代器
d.size(); //返回实际元素个数
push_back(); //在序列的尾部添加一个元素
push_front(); //在序列的头部添加一个元素
pop_back(); //移除容器尾部的元素
pop_front(); //移除容器头部的元素
//遍历
for (auto i = d.begin(); i < d.end(); i++) {
cout << *i << " ";
}
//翻转
reverse(q.begin(),q.end());
单调栈
NGE问题,对序列中每个元素,找到下一个比它大的元素。
我们维护一个栈,表示“待确定NGE的元素”,然后遍历序列。当我们碰上一个新元素,我们知道,越靠近栈顶的元素离新元素位置越近。所以不断比较新元素与栈顶,如果新元素比栈顶大,则可断定新元素就是栈顶的NGE,于是弹出栈顶并继续比较。直到新元素不比栈顶大,再将新元素压入栈。显然,这样形成的栈是单调递减的。
给定项数为n的整数数列,定义函数f(i) 代表数列中第 i 个元素之后第一个大于 ai的元素的下标,若不存在,则 f(i)=0
vector<int> a(maxn),ans(maxn);
stack<int> st;
for(int i=1;i<=n;i++)
{
while(!st.empty()&&a[i]>a[st.top()])
{
ans[st.top()]=i;
st.pop();
}
st.push(i);
}
for(int i=1;i<=n;i++)
cout<<ans[i]<<" ";
单调队列
“如果一个选手比你小还比你强,你就可以退役了。”
单调队列是一种主要用于解决滑动窗口类问题的数据结构,即,在长度为 的序列中,求每个长度为
的区间的区间最值。它的时间复杂度是 O(n)
单调队列的基本思想是,维护一个双向队列(deque),遍历序列,仅当一个元素可能成为某个区间最值时才保留它。
如果要维护区间最大值,我们维护的这个队列总是单调递减的。如果维护区间最小值,那么维护的队列就是单调递增的
vector<int> V(maxn);
//m为滑动窗口长度
deque<int> Q; // 存储的是编号
for (int i = 0; i < n; ++i)
{
if (!Q.empty() && i - Q.front() >= m) // 毕业
Q.pop_front();
while (!Q.empty() && V[Q.back()] < V[i]) // 比新生弱的当场退役(求区间最小值把这里改成>即可)
Q.pop_back();
Q.push_back(i); // 新生入队
if (i >= m - 1)
cout << V[Q.front()] << " ";
}
优先队列priority_queue
优先队列又名二叉堆,是特殊的二叉树。二叉堆分为最大堆和最小堆。
大根堆:父节点的键值总是大于或者等于任何一个子节点的键值
小根堆:父节点的键值总是小于或者等于任何一个子节点的键值
相当于全班同学去排队,每次来一个新的人都矮的排到前面去
左右孩子都比根大的平衡 二叉树
#include<queue>
priority_queue<int> q //队列从大到小排序
priority_queue<int,vector<int>,greater<int>> q //(队列从小到大排序)
//基本操作: (其中q为定义的队列)注意没有队列的q.back()
q.push(x) x为定义的变量,将x压进队列
q.top() 返回队列第一个元素
q.pop() 删除队列第一个元素
q.size() 返回队内元素数量
q.empty() 判断队列是否空,空则返回1,否则返回0;
对顶堆
n个数按顺序加入数组,每次加入的时候就输出中位数
一个大根堆,一个小根堆
缓存交换最佳策略:下一次出现较晚的 先删除
并查集
实现集合的合并与查找
用树来存储一个集合
如果两个点有共同的根,他们就在一个集合里里面
合并两个点所在的集合只需要把一个点的根接到另一个点的根下面就行
按秩合并
路径压缩:将树的所有点连到根上去
如果只有路径压缩,或者只有按秩合并,并查集单次操作的复杂度都是O(log n)
路径压缩+按秩合并的并查集,单次操作的复杂度才是O(a*n),这里的a是Ackerman函数的某个反函数,在很大的范围内,这个函数的值可以看成是不大于4的,所以这里并查集的操作可以看作常数
#include <bits/stdc++.h>
using namespace std;
int n,m;
map<string,int> name;
int fa[20010];
int find(int x)
{
return fa[x]==x?x:fa[x]=find(fa[x]);
}
void merge(int x,int y)
{
fa[find(x)]=find(y);
}
int main()
{
cin>>n>>m;
for(int i=1;i<=n;i++)
{
fa[i]=i;
string s;
cin>>s;
name[s]=i;
}
for(int i=1;i<=m;i++)
{
string s1,s2;
int x;
cin>>x>>s1>>s2;
if(x==1) merge(name[s1],name[s2]);
else
{
if(find(name[s1])!=find(name[s2]))
cout<<0<<endl;
else cout<<1<<endl;
}
}
return 0;
}
堆
堆(heap)分为二叉堆、二项式堆、斐波那契堆,堆是非线性数据结构,相当于一维数组,有两个直接后继。
堆又被称为优先队列,但堆并不是队列。因为队列遵循First in, First out,但是堆是按照元素的优先级取出元素。所以“堆”是实现调度器的理想数据结构。
一般都用数组来表示堆,i为数组的下标,那么该节点的父节点下标为i / 2。它的左右子节点下标分别为2 * i和2 * i + 1。
堆的插入删除
建立堆:数组具有对应的树表示形式。一般情况下,树并不满足堆的条件,通过重新排列元素,可以建立一颗“堆化”的树。
插入一个元素:新元素被插入到即完全二叉树最后的位置,将其和父节点比较。如果新元素比父节点大,那么交换两者。交换之后,继续和新的父节点比较,直至新元素不比父节点大,随后树被更新以恢复堆次序。(其时间复杂度为O(logN)),以上操作称为上溯操作。
void swap(int &x,int &y){int t=x;x=y;y=t;}//交换函数
int heap[N];//定义一个数组来存堆
int siz;//堆的大小
void push(int x){//要插入的数
heap[++siz]=x;
now=siz;
//插入到堆底
while(now){//还没到根节点,还能交换
ll nxt=now>>1;//找到它的父亲
if(heap[nxt]>heap[now])swap(heap[nxt],heap[now]);//父亲比它大,那就交换
else break;//如果比它父亲小,那就代表着插入完成了
now=nxt;//交换
}
return;
}
删除一个元素:删除总是发生在根节点处。树中最后一个元素被用来填补空缺位置,称为暂时根节点,然后将暂时根节点不断和子节点(左右两子节点中大的那一个节点)进行比较,如果他比子节点小,则交换节点位置,直到暂时根节点不小于任何一个子节点,结果树被更新以恢复堆条件。以上操作被称为下溯。
堆的顶端一定是“最大”,最小”的,但是要注意一个点,这里的大和小并不是传统意义下的大和小,它是相对于优先级而言的,当然你也可以把优先级定为传统意义下的大小,但一定要牢记这一点,初学者容易把堆的“大小”直接定义为传统意义下的大小,某些题就不是按数字的大小为优先级来进行堆的操作的
STL自带堆——priority_queue
#include <queue>
struct Node
{
int x,y;
bool operator <(Node a) const { return y < a.y; }
bool operator >(Node a) const { return y > a.y; }
};
priority_queue<Node> A; //大根堆
priority_queue<Node, vector<Node>, greater<Node> > B; //小根堆
//(cmp将结构体以val由大到小排列,组成大根堆)
struct Node
{int adj;
int val;
};
struct cmp
{bool operator()(Node a,Node b) { return a.val > b.val; }
};
priority_queue<Node,vector<Node>,cmp>Q;
//less<class T>这是大顶堆,按值大的优先,值大的在最上面。greater<class T>这是小顶堆,按值小的优先,值小的在最上面。
struct cmp
{
bool operator()(const int &a,const int &b)//这里的&是引用
{
return a>b;//最大堆
return a<b;//最小堆
}
};
priority_queue< int, vector<int>, cmp >
//return就是希望如何排列为true。如果希望由大到小,就将大到小的情况return;
//STL heap包括:
push_heap
//算法:新元素插入在底层的vector的end()处。向上回溯
pop_heap
//算法:把堆顶元素和数值末尾元素调换,向下回溯。
sort_heap
//算法:持续对整个heap做pop_heap操作,每次将操作范围从后向前缩减一个元素。执行过后,原来的heap不再是个合法的heap了。
meak_heap
//算法:找出第一个需要重排的子树头部(n-2)/2,从当前位置向根节点回溯。
#include <queue>
priority_queue<int> q;//这是一个大根堆q
priority_queue<int,vector<int>,greater<int> >q;//这是一个小根堆q
//STL只支持删除堆顶,而不支持删除其他元素
struct node{
int val,rnd;
bool operator < (const node &x) const {
return rnd<x.rnd;
}
}a[100];
二叉堆
二叉堆是完全二叉树或者是近似完全二叉树。
二叉堆分为两种:大顶堆和小顶堆
- 当父节点的键值总是大于或者等于任何一个子节点的键值时为大顶堆
- 当父节点的键值总是小于或者等于任何一个子节点的键值时为小顶堆
任意节点的优先级不小于它的子节点。
所以二叉堆满足:
- 父节点的键值总是大于或者等于(小于或等于)任何一个子节点的键值
- 每个节点的左子树和右子树都是一个二叉堆(都是最大堆或最小堆)
左偏树(可并堆)
左偏树不需要维护左右的平衡,只需要维护权值和npl值来保证查询最值和合并的速度。
npl值,指这个节点到最近一个非满节点的距离。来一张图感受一下左偏树:

const int maxn=1000010;
int n,siz=0,L[maxn],R[maxn],npl[maxn],val[maxn],rt=0;
//分别是操作数,节点数,左子树,右子树,npl(null path length)值,权值,根节点编号
inline int join(int a,int b) {
if (!a) return b;//判断是否为空
if (!b) return a;
if (val[a]>val[b]) swap(a,b);//维护堆性质
R[a]=join(R[a],b);//将b合并到a的右子树上
if (npl[R[a]]>npl[L[a]]) swap(R[a],L[a]);
//维护左偏树性质:npl[r]<npl[l].
npl[a]=npl[R[a]]+1;//npl[now]=npl[r]+1
return a;//返回合并的根
}
inline void pop() {
int qwq=rt;
rt=join(L[rt],R[rt]);
//合并根的左右子树,同时修改根的编号。
//左偏树的删除是惰性删除,而不是直接替换。
L[qwq]=R[qwq]=0;
}
int main(){
npl[0]=-1;
//为了方便计算,一般将npl[0]赋-1。
}
外结点:左儿子或右儿子是空结点的结点。
距离:一个结点 x 的距离distx定义为其子树中与结点 x 最近的外结点到 x 的距离。特别地,定义空结点的距离为 −1 。
基本性质:
左偏树具有堆性质 ,即若其满足小根堆的性质,则对于每个结点 x ,有 vx<=vlc , vx<=vrc 。
左偏树具有左偏性质,即对于每个结点 x ,有 distlc>=distrc 。
基本结论:
结点 x 的距离 distx = distrc+1 。
距离为 n 的左偏树至少有 2n+1−1 个结点。此时该左偏树的形态是一棵满二叉树。
有 n 的结点的左偏树的根节点的距离是 O(log2n) 的。
合并操作:
定义 merge(x,y) 为合并两棵分别以 x,y 为根节点的左偏树,其返回值为合并之后的根节点。
首先不考虑左偏性质,我们描述一下合并两个具有堆性质的树的过程。假设我们要合并的是小根堆。
- 若 vx<=vy ,以 x 作为合并后的根节点;否则以 y 作为合并后的根节点。为避免讨论,若有 vx>vy ,交换 x,y。
- 将 y 与 x 的其中一个儿子合并,用合并后的根节点代替与 y 合并的儿子的位置,并返回 x 。
- 重复以上操作,如果 x 和 y 中有一个为空节点,返回 x+y 。
令 h 为树高, hx+hy 每次都减少了 1,上述过程的时间复杂度是 O(h) 的,当合并的树退化为一条链时,这样做的复杂度是 O(n) 的。要使时间复杂度更优,就要使树合并得更 平衡 。我们有两种方式:
- 每次随机选择 x 的左右儿子进行合并。
- 左偏树。
由于左偏树中左儿子的距离大于右儿子的距离,我们每次将 y 与 x 的右儿子合并。由于左偏树的树高是O(log2n)的,所以单次合并的时间复杂度也是O(log2n)的。
但是,两棵左偏树按照上述方法合并后,可能不再保持左偏树的左偏性质。在每次合并完之后,判断对结点 x是否有 distlc>=distrc,若没有则交换 lc,rc,并维护 x 的距离 distx = distrc+1,即可维护左偏树的左偏性质。
由于合并后的树既满足堆性质又满足左偏性质,所以合并后的树仍然是左偏树。
int merge(int x,int y)
{
if(!x||!y)return x+y;
if(v[y]<v[x])swap(x,y);
rc[x]=merge(rc[x],y);
if(dist[lc[x]]<dist[rc[x]])swap(lc[x],rc[x]);
dist[x]=dist[rc[x]]+1;
return x;
}
插入给定值:
新建一个值等于插入值的结点,将该节点与左偏树合并即可。时间复杂度 O(log2n) 。
求最小值:
由于左偏树的堆性质,左偏树上的最小值为其根节点的值。
删除最小值:
等价于删除左偏树的根节点。合并根节点的左右儿子即可。记得维护已删除结点的信息。
给定一个结点,求其所在左偏树的根节点:
我们可以记录每个结点的父亲结点 fai ,然后暴力跳父亲结点。
int findrt(int x)
{
if(fa[x])return findrt(fa[x]);
return x;
}
注意,虽然左偏树的距离是 O(log2n) 的,但是左偏树的深度最大可以是 O(n) 的,这种做法的复杂度也是 O(n) 的。
上面的代码让你想到了什么?并查集。我们同样可以用 路径压缩 的方式,求一个结点所在左偏树的根节点。
int find(int x){return rt[x]==x?x:rt[x]=find(rt[x]);}
使用这种写法,需要维护 rt[x] 的值。
在合并两个结点 x,y 时,令 rt[x]=rt[y]=merge(x,y) 。
在删除左偏树中的最小值时,令 rt[lc[x]]=rt[rc[x]]=rt[x]=merge(lc[x],rc[x]) ,因为 x 是之前左偏树的根节点,在路径压缩时可能有 rt 的值等于 x,所以 rt[x] 也要指向删除后的根节点。
由于 x 已经被作为中间量使用得不成样子,如果之后还要用到结点 x ,需要新建一个值相同的结点。
路径压缩后,可以在 O(log2n) 的优秀时间复杂度内找到一个点所在左偏树的根节点。
简单红黑树 (一种较高效率的平衡二叉树) set
集合,可以快速查找元素是否在集合里面
#include <set>
set<int> ds; //建立一个名字叫做ds的,元素类型为int的集合
ds.insert(x); //在集合中插入一个元素,如果这个元素已经存在,则什么都不干
ds.erase(x); //在集合中删除元素x,如果这个数不存在,就返回-1
ds.erase(it); //删除集合中地址为it的元素
ds.end();
//返回集合中最后一个元素的下一个元素的地址,不过这个很少直接使用,而是配合其他方法进行比较,以确认某个元素是否存在。
ds.find(x); //查询x在集合中的地址,如果这个数不存在,则返回ds.end()
ds.lower_bound(x); //查询不小于x的最小的数在集合中的地址,如果这个数不存在,则返回ds.end()
ds.upper_bound(x); //查询大于x的最小的数在集合中的地址,如果这个数不存在,则返回ds.end()
ds.empty(); //如果集合是空的,则返回1,否则返回0。
ds.size(); //返回集合中元素的个数
//set容器就是一个用来放数据的容器。里面默认是升序排列,也可以自定义排序。
//set容器里面插入元素不会保留两个相同的元素。你插入100个1,也就是一个1。
///自定义排序重载“()”运算符就好了。和sort自定义cmp一样。调用在初始化的时候就可以了:set<int, cmp> se;。
struct cmp {
bool operator () (const int& u, const int& v) const {
//if (abs(u - v) <= k) return false;
//两个点之间的距离为k的时候直接返回false,表示不用装进去了,就不要这个数了。
return u < v;
}
};
有序集合set
1、简介
set的应用场景和 unordered_set有很大一部分重叠,并且效率低于unordered_set,unordered_set唯一的缺点就是它不是有序的,大致的区别如下:
| STL | 是否有序 | 底层实现 | 增删查改时间复杂度 |
|---|---|---|---|
| set | 是 | 红黑树 | O(log2n) |
| unordered_set | 否 | 哈希表 | O(1) |
2、定义
集合(就可以理解成是数学上的集合),可以理解成键和值相等的键值对,简单定义如下:
set<int> intSet; // (1)整数集合;
set<string> stringSet; // (2)字符串集合;
3、插入
1、insert 函数
set有别于map,它只有一个参数,插入数据的代码如下:
intSet.insert(5);
stringSet.insert("hello");
注意:如果insert执行的时候发现,键已经存在,则第二次insert会失败,但其实对于调用方来说,没有任何影响。
2、操作符 [ ]
也可以利用下标进行操作,如下:
int2int[5] = 1;
string2string["hello"] = "world";
4、删除
直接调用erase函数执行删除,如下:
int2int.erase(5);
string2string.erase("hello");
5、修改
因为对于集合来说,键就是值,所以没有修改的概念。
6、查找
1、精确查找
精确查找就是利用 find函数对给定的键进行查找,由于set本身是一棵平衡二叉树,所以查找的时间复杂度是 的。
如果没有找到,则返回end();如果找到,则可以通过解引用迭代器找到原始的值。
auto iter = intSet.find(5);
if(iter == intSet.end()) {
// 没找到
}else {
cout << *iter << endl;
}
2、模糊查找
模糊查找,查找的是>=key的最小的元素,或者>key的最小的元素;首先,我们插入一堆数据:
intSet.insert(5);
intSet.insert(6);
intSet.insert(8);
intSet.insert(9);
intSet.insert(10);
然后,查找 >=key的最小的键的代码如下:
auto iter = intSet.lower_bound(7);
if(iter == intSet.end()) {
// 没找到,如果找的是 11 就会走到这个逻辑了
}else {
cout << *iter << endl;
}
查找 >key的最小的键的代码如下:
auto iter = intSet.upper_bound(10);
if(iter == intSet.end()) {
// 没找到,> 10 的键不存在
}else {
cout << *iter << endl;
}
通过键值来建立的平衡二叉树 map
二叉搜索树/排序树
左子树<=根<=右子树
自定义下标的数组
map<string,int> mp;
mp["zhangsan"]=4;
for(auto &it:mp)
{
}
#include <map>
map<A,B> ds; //建立一个名字叫做ds,下标类型为A,元素类型为B 的映射表。
//例如map<string,int>就是将一个string映射到int的映射表
ds[A]=B; //将“数组”中下标为A的位置的值变为B,这里的下标可以是任意类型,不一定限定为大于0的整数
//比如map<string,string> ds,就可以进行ds["kkksc03"]="mascot"的操作
ds[A]; //访问这个数组中下标为A 的元素,比如可以进行cout<<ds["kkksc03"]的操作
ds.end(); //返回映射表中最后一个元素的下一个元素的地址。
ds.find(x); //查询x 在映射表中的地址,如果这个数不存在就返回ds.end()
ds.empty(); //如果映射表是空的就返回1,否则返回0
ds.size(); //返回映射表中的元素个数
ds.erase(A); //删除这个数组中下标为A的元素
//在使用ds[A]访问数组下标为A的元素的时候,如果这个数组下表对应的元素不存在时,就会自动创建下标为A,值为默认值的元素
//unordered_map
//unordered_map 容器不会像 map 容器那样对存储的数据进行排序
//unordered_map 容器和 map 容器仅有一点不同,即 map 容器中存储的数据是有序的,而 unordered_map 容器中是无序的
#include <unordered_map>
unordered_map<string, string> umap;
umap.begin() //返回指向容器中第一个键值对的正向迭代器
umap.end() //返回指向容器中最后一个键值对之后位置的正向迭代器
umap.empty() //若容器为空,则返回 true;否则 false
umap.size() //返回当前容器中存有键值对的个数
umap.operator[key]
//该模板类中重载了 [] 运算符,其功能是可以向访问数组中元素那样,只要给定某个键值对的键 key,就可以获取该键对应的值
//注意,如果当前容器中没有以 key 为键的键值对,则其会使用该键向当前容器中插入一个新键值对
umap.find(key) //查找以 key 为键的键值对,如果找到,则返回一个指向该键值对的正向迭代器
//反之,则返回一个指向容器中最后一个键值对之后位置的迭代器(如果 end() 方法返回的迭代器)
umap.count(key) //在容器中查找以 key 键的键值对的个数
umap.insert() //向容器中添加新键值对。
umap.emplace() //向容器中添加新键值对,效率比 insert() 方法高
umap.erase() //删除指定键值对
umap.clear() //清空容器,即删除容器中存储的所有键值对
umap.swap() //交换 2 个 unordered_map 容器存储的键值对,前提是必须保证这 2 个容器的类型完全相等
//使用迭代器输出 umap 容器存储的所有键值对
for (auto iter = umap.begin(); iter != umap.end(); ++iter) {
cout << iter->first << " " << iter->second << endl;
}
//对unordered_map按照value进行排序(或者其他自定义排序)
unordered_map<int,int> umap;
bool cmp(const pair<int,int>& a,const pair<int,int>& b)
{
return a.second<b.second;
}
vector<pair<int,int>> vt;
for(auto x:umap)
{
vt.push_back(x);
}
sort(vt.begin(),vt.end(),cmp);
for (auto iter = vt.begin(); iter != vt.end(); iter++)
{
cout << iter->first << " ";
}
有序键值对map
-
简介:map的应用场景和 unordered_map有很大一部分重叠,并且效率低于unordered_map,unordered_map唯一的缺点就是它不是有序的,大致的区别如下:
STL 是否有序 底层实现 增删查改时间复杂度 map 是 红黑树 O(log2n) unordered_map 否 哈希表 O(1) -
定义:键值对,就是由键和值组成
map<int, int> int2int; //键是整数,值也是整数; map<int, string> int2string; //键是整数,值是字符串; map<string, int> string2int; //键是字符串,值是整数; map<string, string> string2string; //键是字符串,值也是字符串; -
插入:
-
insert函数:
由于 map 本身存储是键值对,所以插入的过程也是插入一个键值对,可以用 std::pair来实现,代码如下:
int2int.insert( std::pair<int, int> (5, 1) ); string2string.insert( std::pair<string, string> ("hello", "world") );以上代码表示在 int2int这个键值对中插入一个键为 5,值为 1 的键值对;在string2string这个键值对中插入一个键为 "hello",值为 "world"的键值对;
注意:如果insert执行的时候发现,键已经存在,则第二次insert会失败。 -
操作符[]
也可以利用下标进行操作,如下:
int2int[5] = 1; string2string["hello"] = "world";
-
-
删除:
直接调用erase函数执行删除,如下:
int2int.erase(5); string2string.erase("hello"); -
修改:
直接利用下标访问进行修改即可,如下:
int2int[5] = 6; int2int[5] = 7; int2int[5] = 8; -
查找
-
精确查找
精确查找就是利用 find函数对给定的键进行查找,由于map本身是一棵平衡二叉树,所以查找的时间复杂度是O(log2n)的。
如果没有找到,则返回end();如果找到,则可以通过first和second获取到键和值。auto iter = int2int.find(5); if(iter == int2int.end()) { // 没找到 }else { // 找到了 cout << iter->first << iter->second << endl; }
-
2.模糊查找
模糊查找,查找的是>=key的最小的键,或者>key的最小的键;首先,我们插入一堆键值对:
int2int.insert( std::pair<int, int> (5, 1) );
int2int.insert( std::pair<int, int> (6, 1) );
int2int.insert( std::pair<int, int> (7, 1) );
int2int.insert( std::pair<int, int> (8, 1) );
int2int.insert( std::pair<int, int> (10, 1) );
然后,查找>=key的最小的键的代码如下:
auto iter = int2int.lower_bound(9);
if(iter == int2int.end()) {
// 当传入 11 时候,就会走到这个逻辑
}else {
// 找到了
cout << iter->first << ',' << iter->second << endl;
}
查找>key的最小的键的代码如下:
auto iter = int2int.upper_bound(5);
if(iter == int2int.end()) {
// 没找到
}else {
// 找到了
cout << iter->first << ',' << iter->second << endl;
}
// 注意,这段代码输出的是 6,1,并非5,1。
可以理解为自定义下标的数组或者是数对的集合,是有序的集合
map<string,int> mp;
map<string,int>::iterator it; //迭代器
mp["张三"]=90; //"自定义下标的数组"
mp.insert(pair<string,int>("李四",95)); //将string和int打包插入平衡二叉树
mp.erase("张三"); //删除张三对应的数组
mp.clear(); //清空数组
mp.empty();
mp.find("张三"); //寻找张三对应的数组的位置,若未找到则返回 map<string,int>::npos
mp.begin();
mp.end();
平衡二叉树 左孩子比根小,右孩子比根大
输入n个字符串,输出重复出现次数最多的字符串
#include <bits/stdc++.h>
#include <map>
using namespace std;
map<string,int> mp;
int main(){
string s;
int n;
cin>>n;
for (int i=1;i<=n;i++){
cin>>s;
mp[s]++;
}
map<string,int>::iterator it;
int maxn=0;
for (it=mp.begin();it!=mp.end();it++){
if (it->second>maxn) {
s=it->first;
maxn=it->second;
}
}
cout<<s;
return 0;
}
//可以用mp[s]来表示对应字符串的个数
//或者
int maxn=0;
for (auto &it :mp){
if (it.second>maxn) {
s=it.first;
maxn=it.second;
}
}
//auto &it:mp 的意思是迭代器it在mp里面自动走一轮
//迭代器用 -> &用.
允许多个相同值的上述两种结构
multiset 和multimap
multiset
C++中multiset容器是STL模板
insert(elem);
//添加一个elem副本,返回新元素位置,无论插入成功与否。
insert(pos, elem);
//添加一个elem元素副本,返回新元素位置,pos为收索起点,提升插入速度。
insert(beg,end);
//将区间[beg,end)所有的元素安插到my_multiset,无返回值。
erase(elem);
//删除与elem相等的所有元素,返回被移除的元素个数。
erase(pos);
//移除迭代器pos所指位置元素,无返回值。
erase(beg,end);
//移除区间[beg,end)所有元素,无返回值。
clear();
//移除所有元素,将容器清空。
begin();
//返回一个随机存取迭代器,指向第一个元素。
end();
//返回一个随机存取迭代器,指向最后一个元素的下一个位置。
rbegin();
//返回一个逆向迭代器,指向逆向迭代的第一个元素。
rend();
//返回一个逆向迭代器,指向逆向迭代的最后一个元素的下一个位置。
count (elem);
//返回元素值为elem的个数。
find(elem);
//返回元素值为elem的第一个元素,如果没有返回end()。
lower_bound(elem);
//返回元素值为elem的第一个可插入位置,也就是元素值 >= elem的第一个元素位置。
upper_bound (elem);
//返回元素值为elem的最后一个可插入位置,也就是元素值 > elem 的第一个元素位置。
equal_range (elem);
//返回elem可插入的第一个位置和最后一个位置,也就是元素值==elem的区间。
//自定义multiset比较器
//不只是int类型,multiset还可以存储其他的类型诸如string类型,结构体(struct)或类(class)类型。
//而我们一般在编程当中遇到的问题经常用到自定义的类型,即struct或class。例如下面的例子:
struct student{
int h,w;
};
multiset<student>s;
//由于multiset并不知道如何去比较一个自定义的类型。
//可以定义multiset里面student类型变量之间的小于关系的含义(这里以h为第一关键字为例),具体过程如下:
//定义一个比较类cmp,cmp内部的operator函数的作用是比较student类型h和w的大小(以h为第一关键字,w为第二关键字):
struct cmp{
bool operator()(const student&s1,const student&s2){
return s1.h<s2.h||s1.h==s2.h&&s1.w<s2.w;
}
};
// 然后将语句"multiset<student>s"改成"multiset<student,cmp>s"这样以后,
就使序列s能够在插入元素的时候自动去比较已有的元素(重载运算符)。
位集
bitset
在结构体内重载运算符
struct ty{
int a,b;
bool operator < (const ty x) const {
return a<x.a;
}
}arr[100];
sort(arr,arr+10);
集合
有时候,不关心数据的前后关系,也不关心数据的层次结构,确定元素只是单纯的被聚集在一起,被称为集合。
模拟
题目让你干啥你干啥,你想干啥就让程序干啥
枚举
优化枚举 的思路: 减少枚举次数
1.选择合适的枚举对象
2.选择合适的枚举方向——方便排除非法或者不是最优的情况
3.选择合适的数据维护方法——转化问题
前缀和
数列区间和 给一个数列,有q次询问,每次询问数列的第li个元素到ri个元素的和
将对区间的查询变为对区间端点的查询
前缀和 可以把区间求和转化为对区间端点的查询 用sum[i]存储前i个数的和 sum[i]=sum[i-1]+a[i] 数列区间的和就等于sum[ri]-sum[li-1]
单次查询复杂度为O(1),总复杂度为O(n+q)
sum[i]即为前缀和
差分
数列修改问题 给一个数列,有q次询问,每次询问数列的第li个元素到ri个元素,都加上一个值ki,求所有修改后这个数列的值
将对区间的修改转化为对区间端点的修改
考虑在区间加的过程中有什么值是在区间端点处发生了变化,而区间内是没有变化的,是每个数与前面一个数的差值
当我们对于第li个到第ri个数加上ki的时候,第li个数与第li-1个数的差值增加了ki,第ri+1与第ri个数的差值减少了ki,而区间内部的相邻两个数的差值是不变的
所以我们可以用数组delta[i]来维护第i个数和前面一个数的差值,然后当需要将[li,ri]区间的每一个数+ki的时候,只需要修改delta[i]和delta[ri+1]即可
在所有的修改操作进行完之后,我们在对于delta[i]求一次前缀和,就可以得到数列的每个元素的值了
用数列delta[i]来维护第i个数和前面一个数的差值的办法叫做差分
差分与前缀和是一对对称操作,对差分数组求前缀和就是原数组,对于前缀和数组求差分就是原数组
有若干个排列在一条直线上的点pi,每个点上有ai个人,找出一个人使得所有人移动到这个点的位置上的总距离最小
应该是中间的那个点
TLE 一般为108次操作
贪心
指的是在对问题求解的时候,总是做出在当前看来是最好的选择。也就是说,不从整体最优上加以考虑,他所做出的是在某种意义上的局部最优解。
能够使用贪心算法的问题都是能够严格证明贪心出的局部最优解就是所求的全局最优解
区间覆盖 在0-L的数轴上有n个区间[li,ri],现在需要选择尽量多的区间,使得两两不相交
对ri进行排序,每次选择ri最小的并且不会造成相交的情况
高精度
高精度加法
#include <bits/stdc++.h>
using namespace std;
string s1,s2;
int a[1000],b[1000];
int len1,len2;
int pre(string s,int a[]){
int len= s.length();
for (int i=0,j=len;i<len;i++,j--)
a[j] = s[i] - '0';
return len;
} //把字符串转为数字
void jia(int a[],int b[]){
int c[1000];
memset(c,0,sizeof(c));
int len = max(len1,len2);
for (int i=1;i<=len;i++){
c[i] = c[i] + a[i] + b[i];
if (c[i]>=10){
c[i+1] += c[i]/10;
c[i] %= 10;
}
}
if (c[len+1]!=0) len++;
for (int i=len;i>=1;i--) cout<<c[i];
}
int main(){
cin>>s1>>s2;
memset(a,0,sizeof(a));
memset(b,0,sizeof(b));
len1 = pre(s1,a);
len2 = pre(s2,b);
jia(a,b);
return 0;
}
//去除前导0写法
#include <bits/stdc++.h>
using namespace std;
string s1,s2;
int a[5000],b[5000];
int len1,len2;
int pre(string s,int a[]){
int len= s.length();
for (int i=0,j=len;i<len;i++,j--)
a[j] = s[i] - '0';
return len;
} //把字符串转为数字
string abs(string s){
int i=0;
string st=s;
while(s[i]=='0'){
st = s.substr(i+1,s.length()-i-1);
i++;
}
return st;
}
void jia(int a[],int b[]){
int c[5010];
memset(c,0,sizeof(c));
int len = max(len1,len2);
for (int i=1;i<=len;i++){
c[i] = c[i] + a[i] + b[i];
if (c[i]>=10){
c[i+1] += c[i]/10;
c[i] %= 10;
}
}
if (c[len+1]!=0) len++;
for (int i=len;i>=1;i--) cout<<c[i];
}
int main(){
cin>>s1>>s2;
s1=abs(s1);
s2=abs(s2);
memset(a,0,sizeof(a));
memset(b,0,sizeof(b));
len1 = pre(s1,a);
len2 = pre(s2,b);
jia(a,b);
cout<<endl;
return 0;
}
高精度减法
#include <bits/stdc++.h>
using namespace std;
string s1,s2;
int a[1000],b[1000];
int len1,len2;
int pre(string s,int a[]){
int len= s.length();
for (int i=0,j=len;i<len;i++,j--)
a[j] = s[i] - '0';
return len;
} //把字符串转为数字
void jian(int a[],int b[]){
int c[1000];
int flag=0;
memset(c,0,sizeof(c));
int len = max (len1,len2);
for (int i=1;i<=len;i++){
if (a[i]==b[i]) flag++;
}
if (flag==len) {cout<<"0"; return;}
for (int i=1;i<=len;i++){
c[i] = c[i] +a[i]-b[i];
if (c[i]<0){
c[i]=c[i]+10;
c[i+1]--;
}
}
while(c[len]==0) len--;
for (int i=len;i>=1;i--) cout<<c[i];
}
bool judge(string s1,string s2){
int l1=s1.length(),l2=s2.length();
if (l1>l2) return 1;
if (l2>l1) return 0;
if (s1>=s2) return 1;
return 0;
}
int main(){
cin>>s1>>s2;
len1 = pre(s1,a);
len2 = pre(s2,b);
if (judge(s1,s2)) jian(a,b);
else{
printf("-");
jian(b,a);
}
return 0;
}
高精度乘法
//该板子在洛谷会RE
#include <bits/stdc++.h>
using namespace std;
string s1,s2;
int a[1000],b[1000];
int len1,len2;
int pre(string s,int a[]){
int len= s.length();
for (int i=0,j=len;i<len;i++,j--)
a[j] = s[i] - '0';
return len;
} //把字符串转为数字
void cheng(int a[],int b[]){
int c[2000];
memset(c,0,sizeof(c));
if ((len1==1&&a[1]==0)||(len2==1&&b[1]==0)) {cout<<"0"; return;}
int len = len1 + len2 -1;
for (int i=1;i<=len1;i++){
for (int j=1;j<=len2;j++){
c[i+j-1] += a[i]*b[j];
}
}
for (int i=1;i<=len;i++){
c[i+1]+=c[i]/10;
c[i]%=10;
}
while(c[len+1]!=0){
len++;
c[len+1]=c[len]/10;
c[len]%=10;
}
for (int i=len;i>=1;i--) cout<<c[i];
}
int main(){
cin>>s1>>s2;
len1 = pre(s1,a);
len2 = pre(s2,b);
cheng(a,b);
return 0;
}
高精度除法
//高精度除以低精度
#include <bits/stdc++.h>
using namespace std;
string s1;
int a[1000];
int len1;
int pre(string s,int a[]){
int len= s.length();
for (int i=0,j=len;i<len;i++,j--)
a[j] = s[i] - '0';
return len;
} //把字符串转为数字
void chu(string s1,int b){
int c[2000];
memset(c,0,sizeof(c));
int len = len1;
int rest = 0;
for (int i=0;i<len;i++){
rest = rest *10 + s1[i] -'0';
c[i] = rest /b ;
rest = rest %b;
}
int pos=0;
while(c[pos]==0) pos++;
for (int i=pos;i<len;i++) cout<<c[i]; //输出商
cout<<endl<<rest; //输出余数
}
int main(){
int x;
cin>>s1>>x;
len1 = pre(s1,a);
chu(s1,x);
return 0;
}
//高精度除以高精度
#include <bits/stdc++.h>
using namespace std;
struct ty
{
int len,num[110];
}shang,yu;
ty change_dao(string s)
{
ty a;
a.len=s.length();
for(int i=0,j=len;i<len;i++,j--)
{
a.num[j]=s[i]-'0';
}
return a;
}
void chu(string s1,string s2)
{
ty b;
b=change(s2);
string rest="";
memset(shang.num,0,sizeof(shang.num));
shang.len=0;
for(int i=0;i<a.length();i++)
{
rest+=a[i];
ty c=change(rest);
int c
while(judge(c,b))
{
c=jian(c,b);
}
}
}
int main()
{
string s1,s2;
cin>>s1>>s2;
chu(s1,s2);
for(int i=shang.len;i>0;i--)
cout<<shang.num[i];
cout<<endl;
for(int i=yu.len;i>0;i--)
cout<<yu.num[i];
}
模拟枚举贪心
#include <bits/stdc++.h>
using namespace std;
struct ty
{
int len,num[110]; //位数
};
string shang,rest;
ty change(string s){
ty a;
memset(a.num,0,sizeof(a.num));
a.len=s.length();
for (int i=0,j=a.len;i<a.len;i++,j--){
a.num[j]=s[i]-'0';
}
return a;
}
bool judge(ty a,ty b){
if (a.len>b.len) return 1;
if (a.len<b.len) return 0;
for (int i=a.len;i>0;i--){
if (a.num[i]>b.num[i]) return 1;
else if (a.num[i]<b.num[i]) return 0;
}
return 1;
}
ty jian(ty a,ty b){
ty c;
memset(c.num,0,sizeof(c.num));
c.len = a.len;
for (int i=1;i<=a.len;i++){
c.num[i] += a.num[i]-b.num[i];
if (c.num[i]<0){
c.num[i]+=10;
c.num[i+1]-=1;
}
}
while(c.num[c.len]==0) c.len--;
return c;
}
string rechange(ty a){
if (a.len == 0) return "0";
string s="";
for (int i=a.len;i>0;i--){
s+=char(a.num[i]+'0');
}
return s;
}
void chu(string a , string s2){
ty b;
b=change(s2);
rest="";
shang="";
for (int i=0;i<a.length();i++){
rest+=a[i];
ty c = change(rest);
int cnt=0;
while(judge(c,b)){
c=jian(c,b);
cnt++;
}
rest = rechange(c);
shang += char(cnt+'0');
}
}
int main()
{
string s1,s2;
cin>>s1>>s2;
chu(s1,s2);
if (rest=="") cout<<"0";
else cout<<rest;
int i=0;
while(shang[i]=='0') i++;
cout<<shang.substr(i,shang.length()-i+1);
cout<<endl;
}
高精度阶乘
#include<bits/stdc++.h>
using namespace std;
const int length=100000;//这个值经过多次调整,才过了10000!
int a[length];
void jiecheng(int n){
a[0] = 1;//首位置为1;
for(int i=2; i<=n; i++)
{//开始计算阶乘
int jinwei = 0;
int j =0;
int temp;
while(j<length)
{//考虑进位及进位的处理
temp = jinwei;
jinwei = (a[j]*i+jinwei)/10;
a[j] = (a[j]*i + temp)%10;
j++;
}
}
int k=length-1;
while(!a[k])
{//将为0的数全跳过,不输出
k--;
}
while(k>=0)
{//输出正确的阶乘结果
cout<<a[k];
k--;
}
}
int main()
{
memset(a,0,sizeof(a));
int n;
cin>>n;
jiecheng(n);
return 0;
}