QuantLib 金融计算——案例之 KRD、Fisher-Weil 久期及久期的解释能力

QuantLib 金融计算——案例之 KRD、Fisher-Weil 久期及久期的解释能力

QuantLib 金融计算——案例之 KRD、Fisher-Weil 久期及久期的解释能力

概述

作为利率风险系列的第四篇，本文将以《Interest Rate Risk Modeling》为蓝本，介绍 Fisher-Weil 久期，并探讨它与 KRD 的关联，最后用线性回归模型简单研究一下久期的解释能力。

cover

有关 KRD 的高级内容请见《《Interest Rate Risk Modeling》阅读笔记——第九章》。

Fisher-Weil 久期的基本概念

上一篇《案例之固息债的价格、久期、凸性和 BPS》中出现的久期和凸性均是基于到期利率（YTM）的风险度量指标，也是最常见的一类债券参数。与此对应，存在着另外一套基于即期利率的风险度量体系，即 Fisher-Weil 久期和凸性。

和麦考利久期的概念一致，Fisher-Weil 久期也是各个现金流的期限关于贴现后现金流的加权平均。不同的是，Fisher-Weil 久期在计算贴现因子时用的是即期利率，而麦考利久期用的是到期利率。此外，Fisher-Weil 久期通常使用连续复利（在连续复利的情况下麦考利久期和修正久期相等），而大多数利率模型也是使用的连续复利。

计算案例

为兼顾历史数据长度以及流动性，下面以 190210 为例，计算 2020-11-10 这一天的 Fisher-Weil 久期和 KRD，随后会用最近一年的利率和价格数据做久期的实证分析，数据均来自上清所。

首先从中国货币网查询债券的基本信息，用以配置 FixedRateBond 对象。

债券起息日：2019-05-21
到期兑付日：2029-05-21
债券期限：10 年
面值(元)：100.00
计息基准：A/A
息票类型：附息式固定利率
付息频率：年
票面利率（%）：3.65
结算方式：T+1

计算 KRD 的过程基本上照搬上一篇文章的代码，个别细节略有不同。

import QuantLib as ql
import prettytable as pt
import seaborn as sns
import numpy as np
import pandas as pd
import statsmodels.api as sm

today = ql.Date(10, ql.November, 2020)
ql.Settings.instance().evaluationDate = today

effectiveDate = ql.Date(21, ql.May, 2019)
terminationDate = ql.Date(21, ql.May, 2029)
tenor = ql.Period(1, ql.Years)
calendar = ql.China(ql.China.IB)
convention = ql.Unadjusted
terminationDateConvention = convention
rule = ql.DateGeneration.Backward
endOfMonth = False

settlementDays = 1
faceAmount = 100.0

schedule = ql.Schedule(
    effectiveDate,
    terminationDate,
    tenor,
    calendar,
    convention,
    terminationDateConvention,
    rule,
    endOfMonth)

scheduleEx = ql.Schedule(
    effectiveDate,
    ql.Date(21, ql.May, 2041),
    tenor,
    calendar,
    convention,
    terminationDateConvention,
    rule,
    endOfMonth)

coupons = ql.DoubleVector(1)
coupons[0] = 3.65 / 100.0
accrualDayCounter = ql.ActualActual(
    ql.ActualActual.Bond, scheduleEx)
paymentConvention = ql.Unadjusted

bond = ql.FixedRateBond(
    settlementDays,
    faceAmount,
    schedule,
    coupons,
    accrualDayCounter,
    paymentConvention)

spotRates = np.array(
    [1.0,
     1.71078231001656, 2.56940621917972, 2.83503053129122, 3.08812284213447,
     3.27817582743435, 3.36929632559628, 3.38215484755107, 3.48805389778613,
     3.54897231967215, 3.70182895980812, 3.70828526340311, 3.65884055155817,
     3.96859895108321, 4.00107855792347]) / 100.0

tenors = ql.DateVector()
tenors.append(today)
tenors.append(today + ql.Period(1, ql.Days))
tenors.append(today + ql.Period(6, ql.Months))
tenors.append(today + ql.Period(1, ql.Years))
tenors.append(today + ql.Period(2, ql.Years))
tenors.append(today + ql.Period(3, ql.Years))
tenors.append(today + ql.Period(4, ql.Years))
tenors.append(today + ql.Period(5, ql.Years))
tenors.append(today + ql.Period(6, ql.Years))
tenors.append(today + ql.Period(7, ql.Years))
tenors.append(today + ql.Period(8, ql.Years))
tenors.append(today + ql.Period(9, ql.Years))
tenors.append(today + ql.Period(10, ql.Years))
tenors.append(today + ql.Period(15, ql.Years))
tenors.append(today + ql.Period(20, ql.Years))

compounding = ql.Continuous
frequency = ql.Annual

spotCurve = ql.YieldTermStructureHandle(
    ql.LogLinearZeroCurve(
        tenors,
        spotRates,
        accrualDayCounter,
        calendar,
        ql.LogLinear(),
        compounding))

关于 scheduleEx，请看这里。

spotRates 里面是 2020-11-10 这天的即期利率（根据上清所的数据转换成连续复利），用于构造即期期限结构。spotRates 中的第一个元素通常用于为插值计算提供边界点，表示今天的利率值。这里采用 LogLinear 插值，所以可以用 1.0，若用 Linear 插值，也可以用 0.0。tenors 中的第一个元素通常用于为期限结构提供基准日期，一般来说就是估值日期当天。由于后面提供了隔夜利率，spotRates[0] 这个数其实不参与计算，但必须有，以便和 tenors 对齐。

下面是计算 KRD 的过程。（有点儿繁琐，感兴趣的读者可以尝试改写成一个简单的 for 循环）

initValue = 0.0
rate1d = ql.SimpleQuote(initValue)
rate6m = ql.SimpleQuote(initValue)
rate1y = ql.SimpleQuote(initValue)
rate2y = ql.SimpleQuote(initValue)
rate3y = ql.SimpleQuote(initValue)
rate4y = ql.SimpleQuote(initValue)
rate5y = ql.SimpleQuote(initValue)
rate6y = ql.SimpleQuote(initValue)
rate7y = ql.SimpleQuote(initValue)
rate8y = ql.SimpleQuote(initValue)
rate9y = ql.SimpleQuote(initValue)
rate10y = ql.SimpleQuote(initValue)
rate15y = ql.SimpleQuote(initValue)
rate20y = ql.SimpleQuote(initValue)

rate1dHandle = ql.QuoteHandle(rate1d)
rate6mHandle = ql.QuoteHandle(rate6m)
rate1yHandle = ql.QuoteHandle(rate1y)
rate2yHandle = ql.QuoteHandle(rate2y)
rate3yHandle = ql.QuoteHandle(rate3y)
rate4yHandle = ql.QuoteHandle(rate4y)
rate5yHandle = ql.QuoteHandle(rate5y)
rate6yHandle = ql.QuoteHandle(rate6y)
rate7yHandle = ql.QuoteHandle(rate7y)
rate8yHandle = ql.QuoteHandle(rate8y)
rate9yHandle = ql.QuoteHandle(rate9y)
rate10yHandle = ql.QuoteHandle(rate10y)
rate15yHandle = ql.QuoteHandle(rate15y)
rate20yHandle = ql.QuoteHandle(rate20y)

spreads = ql.QuoteHandleVector()
spreads.append(rate1dHandle)
spreads.append(rate6mHandle)
spreads.append(rate1yHandle)
spreads.append(rate2yHandle)
spreads.append(rate3yHandle)
spreads.append(rate4yHandle)
spreads.append(rate5yHandle)
spreads.append(rate6yHandle)
spreads.append(rate7yHandle)
spreads.append(rate8yHandle)
spreads.append(rate9yHandle)
spreads.append(rate10yHandle)
spreads.append(rate15yHandle)
spreads.append(rate20yHandle)

termStructure = ql.YieldTermStructureHandle(
    ql.SpreadedLinearZeroInterpolatedTermStructure(
        spotCurve,
        spreads,
        tenors[1:],
        compounding,
        frequency,
        accrualDayCounter))

engine = ql.DiscountingBondEngine(termStructure)
bond.setPricingEngine(engine)

dirtyPrice = bond.dirtyPrice()

tab = pt.PrettyTable(['item', 'value'])

# calculate KRDs

bp = 0.01 / 100.0
krdSum = 0.0
krds = []
times = []

# 1d KRD
rate1d.setValue(bp)
dirtyPrice1 = bond.dirtyPrice()
rate1d.setValue(-bp)
dirtyPrice2 = bond.dirtyPrice()
rate1d.setValue(initValue)
krd1d = -(dirtyPrice1 - dirtyPrice2) / (2.0 * bp * dirtyPrice)
krdSum += krd1d
krds.append(krd1d)
times.append(0.00274)  # 1.0 / 365

tab.add_row(['krd1d', krd1d])

# 6m KRD
rate6m.setValue(bp)
dirtyPrice1 = bond.dirtyPrice()
rate6m.setValue(-bp)
dirtyPrice2 = bond.dirtyPrice()
rate6m.setValue(initValue)
krd6m = -(dirtyPrice1 - dirtyPrice2) / (2.0 * bp * dirtyPrice)
krdSum += krd6m
krds.append(krd6m)
times.append(0.5)

tab.add_row(['krd6m', krd6m])

# 1y KRD
rate1y.setValue(bp)
dirtyPrice1 = bond.dirtyPrice()
rate1y.setValue(-bp)
dirtyPrice2 = bond.dirtyPrice()
rate1y.setValue(initValue)
krd1y = -(dirtyPrice1 - dirtyPrice2) / (2.0 * bp * dirtyPrice)
krdSum += krd1y
krds.append(krd1y)
times.append(1.0)

tab.add_row(['krd1y', krd1y])

# 2y KRD
rate2y.setValue(bp)
dirtyPrice1 = bond.dirtyPrice()
rate2y.setValue(-bp)
dirtyPrice2 = bond.dirtyPrice()
rate2y.setValue(initValue)
krd2y = -(dirtyPrice1 - dirtyPrice2) / (2.0 * bp * dirtyPrice)
krdSum += krd2y
krds.append(krd2y)
times.append(2.0)

tab.add_row(['krd2y', krd2y])

# 3y KRD
rate3y.setValue(bp)
dirtyPrice1 = bond.dirtyPrice()
rate3y.setValue(-bp)
dirtyPrice2 = bond.dirtyPrice()
rate3y.setValue(initValue)
krd3y = -(dirtyPrice1 - dirtyPrice2) / (2.0 * bp * dirtyPrice)
krdSum += krd3y
krds.append(krd3y)
times.append(3.0)

tab.add_row(['krd3y', krd3y])

# 4y KRD
rate4y.setValue(bp)
dirtyPrice1 = bond.dirtyPrice()
rate4y.setValue(-bp)
dirtyPrice2 = bond.dirtyPrice()
rate4y.setValue(initValue)
krd4y = -(dirtyPrice1 - dirtyPrice2) / (2.0 * bp * dirtyPrice)
krdSum += krd4y
krds.append(krd4y)
times.append(4.0)

tab.add_row(['krd4y', krd4y])

# 5y KRD
rate5y.setValue(bp)
dirtyPrice1 = bond.dirtyPrice()
rate5y.setValue(-bp)
dirtyPrice2 = bond.dirtyPrice()
rate5y.setValue(initValue)
krd5y = -(dirtyPrice1 - dirtyPrice2) / (2.0 * bp * dirtyPrice)
krdSum += krd5y
krds.append(krd5y)
times.append(5.0)

tab.add_row(['krd5y', krd5y])

# 6y KRD
rate6y.setValue(bp)
dirtyPrice1 = bond.dirtyPrice()
rate6y.setValue(-bp)
dirtyPrice2 = bond.dirtyPrice()
rate6y.setValue(initValue)
krd6y = -(dirtyPrice1 - dirtyPrice2) / (2.0 * bp * dirtyPrice)
krdSum += krd6y
krds.append(krd6y)
times.append(6.0)

tab.add_row(['krd6y', krd6y])

# 7y KRD
rate7y.setValue(bp)
dirtyPrice1 = bond.dirtyPrice()
rate7y.setValue(-bp)
dirtyPrice2 = bond.dirtyPrice()
rate7y.setValue(initValue)
krd7y = -(dirtyPrice1 - dirtyPrice2) / (2.0 * bp * dirtyPrice)
krdSum += krd7y
krds.append(krd7y)
times.append(7.0)

tab.add_row(['krd7y', krd7y])

# 8y KRD
rate8y.setValue(bp)
dirtyPrice1 = bond.dirtyPrice()
rate8y.setValue(-bp)
dirtyPrice2 = bond.dirtyPrice()
rate8y.setValue(initValue)
krd8y = -(dirtyPrice1 - dirtyPrice2) / (2.0 * bp * dirtyPrice)
krdSum += krd8y
krds.append(krd8y)
times.append(8.0)

tab.add_row(['krd8y', krd8y])

# 9y KRD
rate9y.setValue(bp)
dirtyPrice1 = bond.dirtyPrice()
rate9y.setValue(-bp)
dirtyPrice2 = bond.dirtyPrice()
rate9y.setValue(initValue)
krd9y = -(dirtyPrice1 - dirtyPrice2) / (2.0 * bp * dirtyPrice)
krdSum += krd9y
krds.append(krd9y)
times.append(9.0)

tab.add_row(['krd9y', krd9y])

# 10y KRD
rate10y.setValue(bp)
dirtyPrice1 = bond.dirtyPrice()
rate10y.setValue(-bp)
dirtyPrice2 = bond.dirtyPrice()
rate10y.setValue(initValue)
krd10y = -(dirtyPrice1 - dirtyPrice2) / (2.0 * bp * dirtyPrice)
krdSum += krd10y
krds.append(krd10y)
times.append(10.0)

tab.add_row(['krd10y', krd10y])

# 15y KRD
rate15y.setValue(bp)
dirtyPrice1 = bond.dirtyPrice()
rate15y.setValue(-bp)
dirtyPrice2 = bond.dirtyPrice()
rate15y.setValue(initValue)
krd15y = -(dirtyPrice1 - dirtyPrice2) / (2.0 * bp * dirtyPrice)
krdSum += krd15y
krds.append(krd15y)
times.append(15.0)

tab.add_row(['krd15y', krd15y])

# 20y KRD
rate20y.setValue(bp)
dirtyPrice1 = bond.dirtyPrice()
rate20y.setValue(-bp)
dirtyPrice2 = bond.dirtyPrice()
rate20y.setValue(initValue)
krd20y = -(dirtyPrice1 - dirtyPrice2) / (2.0 * bp * dirtyPrice)
krdSum += krd20y
krds.append(krd20y)
times.append(20.0)

tab.add_row(['krd20y', krd20y])

tab.add_row(['krdSum', krdSum])


def FisherWeilDuration(bond: ql.FixedRateBond,
                       term_structure: ql.YieldTermStructureHandle,
                       settlement: ql.Date = ql.Date()):
    if settlement == ql.Date():
        settlement = bond.settlementDate()

    fwd = 0.0
    p = bond.dirtyPrice()
    dc = bond.dayCounter()

    for cf in bond.cashflows():
        if cf.date() > settlement:
            df = term_structure.discount(cf.date())
            t = dc.yearFraction(settlement, cf.date())

            fwd += t * df * cf.amount()

    return fwd / p


fwd = FisherWeilDuration(bond, spotCurve)

tab.add_row(['fwd', fwd])
tab.add_row(['dirty', dirtyPrice])
tab.add_row(['mkt', 101.0751])

tab.float_format = '.8'

print(tab)

'''
+--------+--------------+
|  item  |    value     |
+--------+--------------+
| krd1d  | -0.00273973  |
| krd6m  |  0.01761345  |
| krd1y  |  0.02607589  |
| krd2y  |  0.06751827  |
| krd3y  |  0.09790298  |
| krd4y  |  0.12608806  |
| krd5y  |  0.15196510  |
| krd6y  |  0.17540198  |
| krd7y  |  0.19649419  |
| krd8y  |  3.12947679  |
| krd9y  |  3.35232738  |
| krd10y | -0.00000000  |
| krd15y | -0.00000000  |
| krd20y | -0.00000000  |
| krdSum |  7.33812436  |
|  fwd   |  7.33778022  |
| dirty  | 101.11162007 |
|  mkt   | 101.07510000 |
+--------+--------------+
'''

sns.lineplot(
    x=times, y=krds, marker='o')

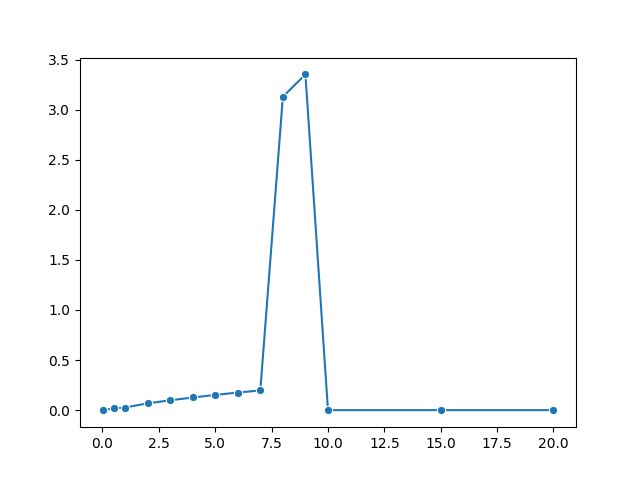
债券最大一笔现金流的期限落在 8～9 年之间，所 8 和 9 年期利率的敏感性最大，10 年以上的利率则完全没有影响。隔夜利率有着极其微弱的负久期比较让人意外。

FisherWeilDuration 函数用来计算 Fisher-Weil 久期，其逻辑完全参照 BondFunctions::duration 方法。Fisher-Weil 久期隐含地假设了曲线水平移动，因此 KRD 的和应该和 Fisher-Weil 久期极为接近，计算结果也证实了这一点。

可以看到，根据期限结构计算出的“理论价格”和实际的市场价格有一定的出入，即期期限结构通常由交易数据拟合得到，误差在所难免。

久期解释能力的实证

之前说到了 Fisher-Weil 久期隐含地假设了曲线水平移动，下面简单研究一下曲线水平移动能在多大程度上解释债券价格的变化。

选取最近一年的即期利率（转换成连续复利），关键期限分别是隔夜、半年、1 至 10 年、15 年和 20 年，计算每天的利率变化，并把关键期限利率变化的平均值视作曲线的水平移动量。再根据全价计算出债券每天的回报率，两者建立线性回归模型，预计得到的回归系数应该和 Fisher-Weil 久期大体相等。

# Empirical Test

ratesChg = pd.read_csv(
    'rates_chg.csv', parse_dates=True, index_col='date')

returns = pd.read_csv(
    'returns.csv', parse_dates=True, index_col='date')

levelChgs = pd.DataFrame(
    ratesChg.values.mean(1), index=ratesChg.index, columns=['levelChgs'])

ols = sm.OLS(endog=returns, exog=sm.add_constant(levelChgs))
olsEst = ols.fit()

print(olsEst.summary())

sns.regplot(
    x=levelChgs, y=returns)

'''
                            OLS Regression Results
==============================================================================
Dep. Variable:                 return   R-squared:                       0.532
Model:                            OLS   Adj. R-squared:                  0.530
Method:                 Least Squares   F-statistic:                     279.9
Date:                Sat, 14 Nov 2020   Prob (F-statistic):           1.79e-42
Time:                        23:32:01   Log-Likelihood:                 83.522
No. Observations:                 248   AIC:                            -163.0
Df Residuals:                     246   BIC:                            -156.0
Df Model:                           1
Covariance Type:            nonrobust
==============================================================================
                 coef    std err          t      P>|t|      [0.025      0.975]
------------------------------------------------------------------------------
const          0.0121      0.011      1.096      0.274      -0.010       0.034
levelChgs     -7.3574      0.440    -16.731      0.000      -8.224      -6.491
==============================================================================
Omnibus:                       28.630   Durbin-Watson:                   2.172
Prob(Omnibus):                  0.000   Jarque-Bera (JB):              155.775
Skew:                          -0.048   Prob(JB):                     1.49e-34
Kurtosis:                       6.881   Cond. No.                         39.9
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
'''

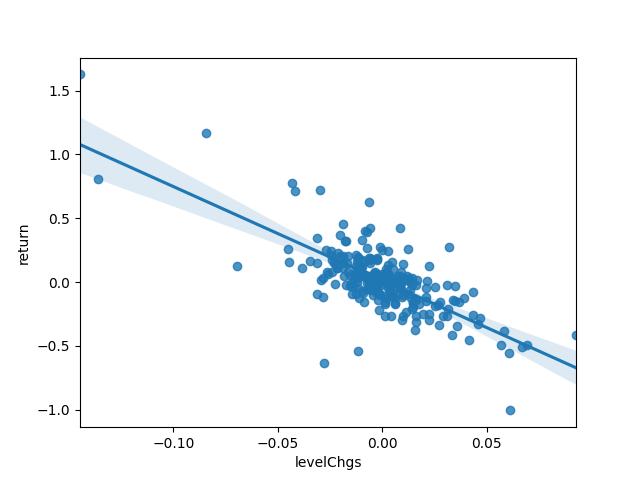
散点图非常完美。

最终的回归系数确实和 Fisher-Weil 久期大体相等，但 \(R^2\) 约等于 50%，也就是说当前的“水平因子”（或者说久期）仅能解释一半的回报率变化。不可解释的本分可能来自于

模型价格与市场价格之间的差异（市场有效性不足）
水平因子的二阶敏感性，以及
其他曲线形态因子的一（二）阶敏感性。

其他曲线形态因子的一阶敏感性则是下一篇的主题——主成分久期（PCD）。

扩展阅读

《QuantLib 金融计算》系列合集

posted @ 2020-11-16 23:38 xuruilong100 阅读(2018) 评论(0) 编辑收藏举报

刷新页面返回顶部