《Interest Rate Risk Modeling》阅读笔记——第五章：久期向量模型
第五章：久期向量模型
思维导图
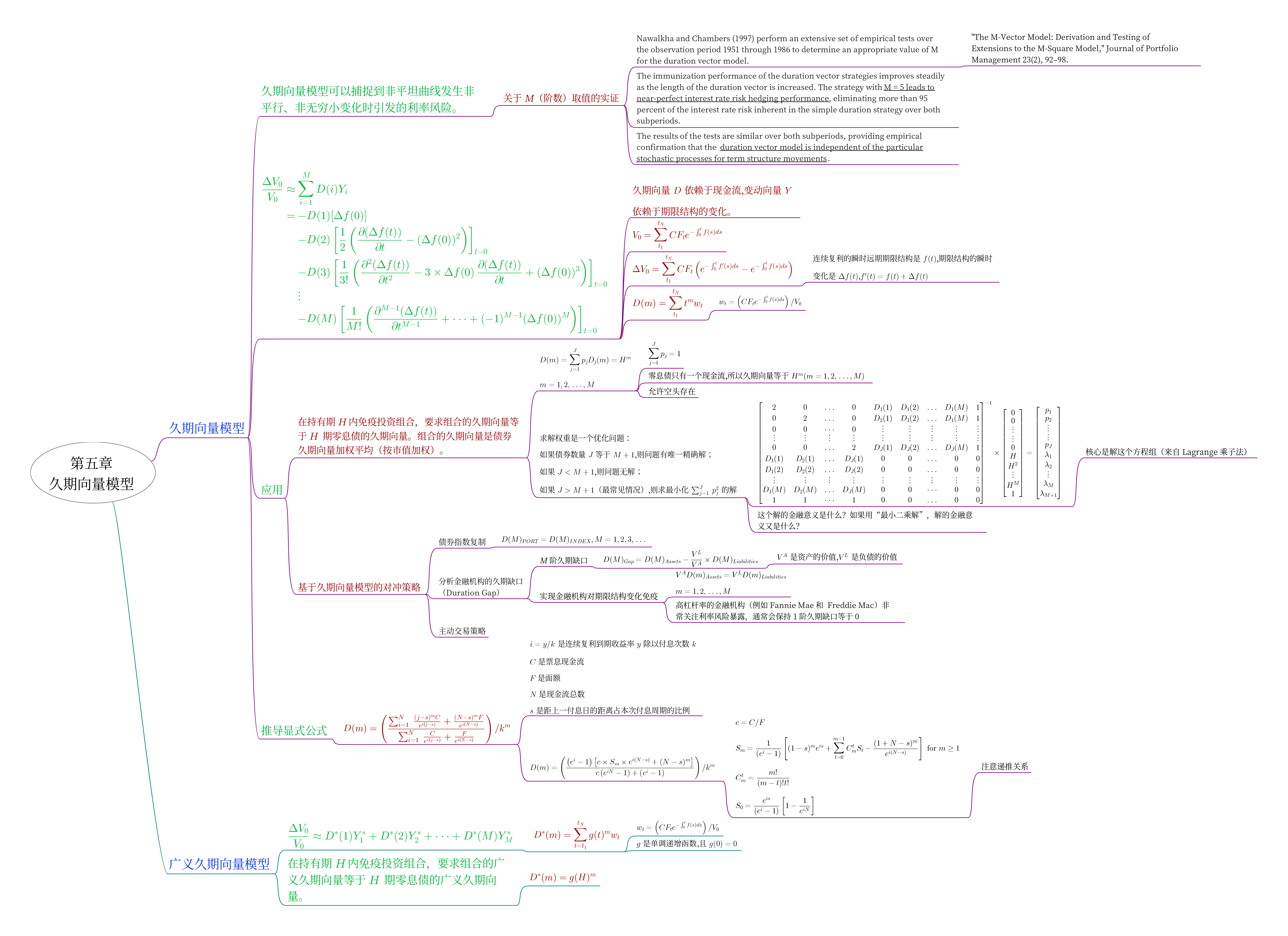
久期向量的推导
\[V_0 = \sum_{t=t_1}^{t_n} CF_t e^{-\int_0^t f(s)ds}
\]
\[V^\prime_0 = \sum_{t=t_1}^{t_n} CF_t e^{-\int_0^t f^\prime(s)ds}
\]
\[\begin{aligned}
\frac{V_0^{\prime} - V_0}{V_0}
&= \frac{1}{V_0 } \sum_{t=t_1}^{t_n} CF_t (e^{-\int_0^t f^{\prime}(s)ds} - e^{-\int_0^t f(s)ds})\\
&=\frac{1}{V_0}\sum_{t=t_1}^{t_n} CF_te^{-\int_0^t f(s)ds}(e^{-\int_0^t \Delta f(s)ds}-1)\\
&=\sum_{t=t_1}^{t_n} w_t(e^{-\int_0^t \Delta f(s)ds}-1)
\end{aligned}
\]
\[h(t) = e^{-\int_0^t \Delta f(s)ds}
\]
久期向量
对 \(h(t)\) 在 \(0\) 做 Taylor 展开：
\[\begin{aligned}
h(t) &= e^{-\int_0^t \Delta f(s)ds}\\
&= h(0) + \frac{1}{1!}\frac{dh}{dt}|_{t=0}t + \frac{1}{2!}\frac{d^2h}{dt^2}|_{t=0}t^2 + \cdots + \frac{1}{n!}\frac{d^nh}{dt^n}|_{t=0}t^n+ \varepsilon\\
&= 1 + \frac{1}{1!}t\left(-\Delta f(t)\right)|_{t=0} +
\frac{1}{2!}t^2\left(\Delta f(t)^2 - \frac{d\Delta f}{dt}\right)|_{t=0} + \cdots +
\frac{1}{n!}t^n\left(-\frac{d^{n-1}\Delta f}{dt^{n-1}} + \cdots + (-1)^{n}\Delta f(t)^n\right)|_{t=0}+ \varepsilon\\
\end{aligned}
\]
\(h(t)\) 可以表示为 \(t\) 级数与期限结构变化（\(\Delta f\)）的组合，进而得到久期向量的表达式：
\[D(m) =\sum_{t=t_1}^{t_n} w_t t^m
\]
广义久期向量
\(g(s)\) 是一个单调递增函数，且 \(g(0) = 0\)。
如果令 \(x = g(s)\)，于是有 \(s = g^{-1}(x)\)，那么
\[\begin{aligned}
h(t) &= e^{-\int_0^t \Delta f(s)ds}\\
&=e^{-\int_0^{g(t)} \Delta f(g^{-1}(x))\frac{1}{g\prime(g^{-1}(x))} dx}
\end{aligned}
\]
令 \(k(x) = \Delta f(g^{-1}(x))\frac{1}{g\prime(g^{-1}(x))}\)，参照上面的过程，对
\[e^{-\int_0^{g(t)} \Delta f(g^{-1}(x))\frac{1}{g\prime(g^{-1}(x))} dx}
\]
在 \(0\) 做 Taylor 展开，那么 \(h(t)\) 可以表示为 \(g(t)\) 级数与期限结构变化（\(k\)）的组合，进而得到广义久期向量的表达式：
\[D^*(m) =\sum_{t=t_1}^{t_n} w_t g(t)^m
\]
一些想法
- 广义久期向量的想法类似于对时间做了“测度变换”。
- 目前的久期向量免疫算法得到的权重保证 \(L^2\) 范数最小，如果要求解是“稀疏的”，可以考虑用 \(L^1\) 范数最小的解。
- 解的稀疏性对指数复制来说可能是个有意义的问题。
★ 持续学习 ★ 坚持创作 ★
