QuantLib 金融计算——案例之普通欧式期权分析

目录

如果未做特别说明，文中的程序都是 python3 代码。

QuantLib 金融计算——案例之普通欧式期权分析

载入 QuantLib 和其他包：

import QuantLib as ql
import numpy as np
import pandas as pd

print(ql.__version__)

1.15

概述

从金融工程中最简单的案例——“普通欧式期权公式法定价”入手，介绍 QuantLib 中期权分析的基本组件，以及如何将这些组件拼接成为一个完整的计算流程。

普通欧式期权公式法定价

采用《期权、期货及其他衍生产品（第 7 版）》第 17 章中的例子：

  • 类型：普通欧式看涨期权
  • 当前价格：49$
  • 敲定价格：50$
  • 无风险利率：5%
  • 年化波动率：20%
  • 期限：20 周

使用 BS 公式为上述期权定价，并计算希腊值。

1. 配置期权合约条款

# 配置日期计算条款
calendar = ql.UnitedStates(ql.UnitedStates.NYSE)
dayCounter = ql.Actual365Fixed(ql.Actual365Fixed.Standard)

todayDate = ql.Date(11, ql.July, 2019)
maturity = todayDate + ql.Period(20, ql.Weeks)
settlementDate = todayDate

# 配置期权参数
stock = 49
strike = 50
riskFreeRate = 0.05
volatility = 0.2

# 配置全局估值日期
ql.Settings.instance().evaluationDate = todayDate

2. 构建期权对象

# 配置行权条款
europeanExercise = ql.EuropeanExercise(maturity)
optionType = ql.Option.Call
payoff = ql.PlainVanillaPayoff(
    type=optionType, strike=strike)

# 构建期权对象
europeanOption = ql.VanillaOption(
    payoff=payoff,
    exercise=europeanExercise)

3. 配置定价引擎

underlying = ql.SimpleQuote(stock)
underlyingH = ql.QuoteHandle(underlying)

# 无风险利率的期限结构
flatRiskFreeTS = ql.YieldTermStructureHandle(
    ql.FlatForward(
        settlementDate, riskFreeRate, dayCounter))

# 波动率的期限结构
flatVolTS = ql.BlackVolTermStructureHandle(
    ql.BlackConstantVol(
        settlementDate, calendar,
        volatility, dayCounter))

# 构建 BS 过程
bsProcess = ql.BlackScholesProcess(
    s0=underlyingH,
    riskFreeTS=flatRiskFreeTS,
    volTS=flatVolTS)

# 基于 BS 过程的公式定价引擎
pricingEngine = ql.AnalyticEuropeanEngine(
    bsProcess)

europeanOption.setPricingEngine(pricingEngine)

4. 计算

# RESULTS

print("Option value =", europeanOption.NPV())
print("Delta value  =", europeanOption.delta())
print("Theta value  =", europeanOption.theta())
print("Theta perday =", europeanOption.thetaPerDay())
print("Gamma value  =", europeanOption.gamma())
print("Vega value   =", europeanOption.vega())
print("Rho value    =", europeanOption.rho())

Option value = 2.395988448539984
Delta value  = 0.5213970624832108
Theta value  = -4.309457134907618
Theta perday = -0.011806731876459226
Gamma value  = 0.06563585494066533
Vega value   = 12.089225358769994
Rho value    = 8.88039853654583

题外话：天数计算规则

上述例子中的计算结果和书中给出的结果略有出入，依经验判断，最有可能造成计算不一致的原因是“天数计算规则的不一致”。

详细来说，书中期权的期限是 20 周，作者认为 20 周等于 0.3846 年，可能的依据有：

  • \(20 \times 7 / 364(\text{not } 365) \approx 0.3846\) （即 Actual/364）或
  • \(20 \times 5(\text{weekday}) / [52(\approx 365/7)\times 5(\text{weekday})] \approx 0.3846\)

目前，QuantLib 中并不支持这两种天数计算规则。例子中出现的规则 Actual365Fixed(Actual365Fixed.Standard) 认为 20 周等于 0.38356 年：

print(dayCounter.yearFraction(settlementDate, maturity))
# 0.3835616438356164

对于期权来说，天数计算规则的影响可能微不足道，但是对于固定收益类金融工具及其衍生品来说，天数计算规则的选择至关重要，“失之毫厘，谬以千里”。

Quote 带来的便利

QuantLib 中有相当多的组件接受 Handle 类型的参数，而这些参数通常持有一个 Quote 类型的变量。借助“观察者模式”，用户修改 Quote 类型变量的值将会自动通知相关组件，并使其重新进行性计算，而无需再次构建一遍计算流程。对于某些用途来讲，这带来了相当大的便利。

# USE QUOTE

stock_array = np.arange(
    start=30, stop=70, step=0.01)

NPV = np.array([np.nan] * len(stock_array))
delta = np.array([np.nan] * len(stock_array))
theta = np.array([np.nan] * len(stock_array))
# thetaPerDay = np.array([np.nan] * len(stock_array))
gamma = np.array([np.nan] * len(stock_array))
vega = np.array([np.nan] * len(stock_array))
rho = np.array([np.nan] * len(stock_array))

for i, v in enumerate(stock_array):
    # 重置 Quote 对象的值
    underlying.setValue(v)

    # 无须再次配置计算流程，直接计算
    NPV[i] = europeanOption.NPV()
    delta[i] = europeanOption.delta()
    theta[i] = europeanOption.theta()
    # thetaPerDay[i] = europeanOption.thetaPerDay()
    gamma[i] = europeanOption.gamma()
    vega[i] = europeanOption.vega()
    rho[i] = europeanOption.rho()

result = pd.DataFrame(
    data=dict(
        NPV=NPV,
        delta=delta,
        theta=theta,
        # thetaPerDay=thetaPerDay,
        gamma=gamma,
        vega=vega, rho=rho),
    index=stock_array)

result.plot(subplots=True)

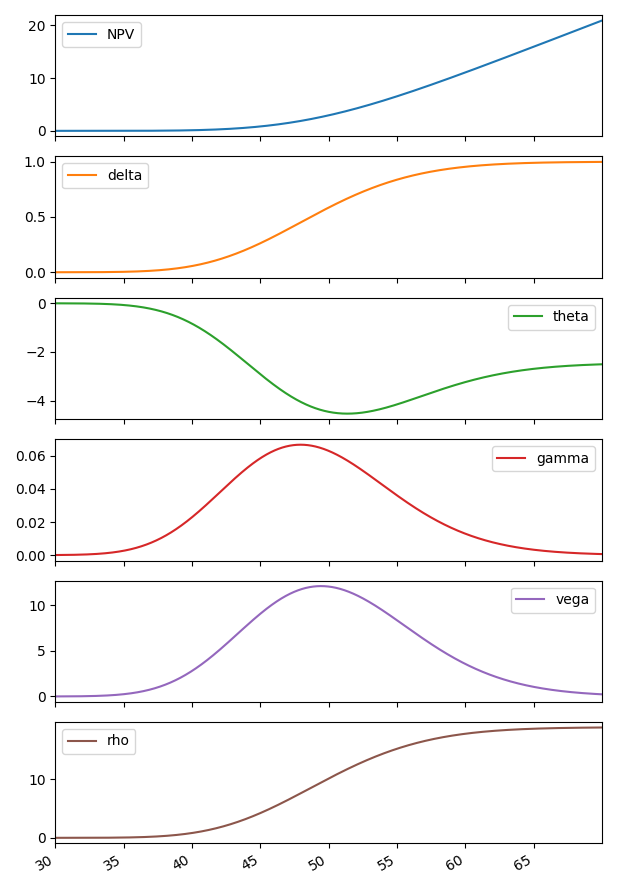
总结

下面用一副图显示上述例子中的若干变量如何汇聚成一个计算流程：

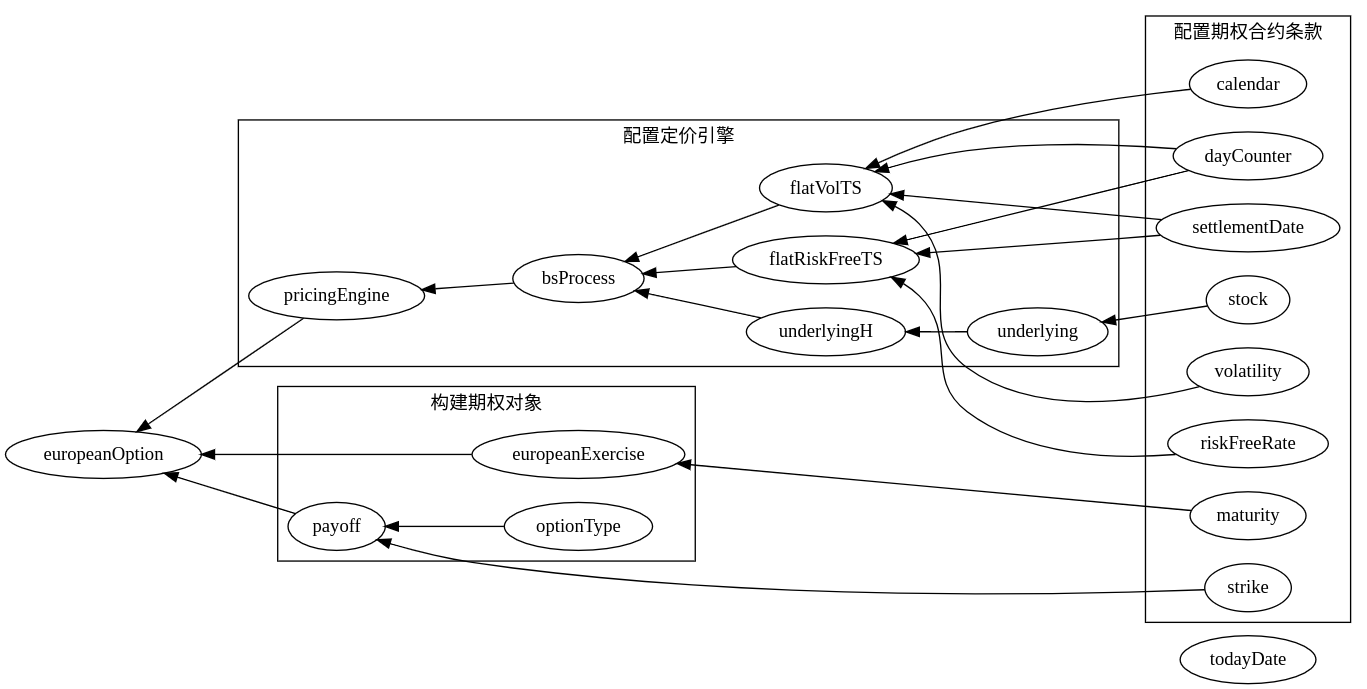
扩展阅读

《QuantLib 金融计算》系列合集

posted @ 2019-07-14 17:03  xuruilong100  阅读(5245)  评论(5)  编辑  收藏  举报