QuantLib 金融计算——随机过程之 Heston 过程

目录

• QuantLib 金融计算——随机过程之 Heston 过程
  • Heston 过程
  • 参考文献
  • 扩展阅读

如果未做特别说明，文中的程序都是 Python3 代码。

QuantLib 金融计算——随机过程之 Heston 过程

载入模块

import QuantLib as ql
import pandas as pd
import numpy as np
import seaborn as sn

print(ql.__version__)

1.12

Heston 过程

著名的 Heston 模型描述了下列 SDE：

\[\begin{aligned} d S_t & = \mu S_t d t + \sqrt { V_t } S_t d W_t^S \\ d V_t & = \kappa \left( \theta - V_t \right) d t + \sigma \sqrt { V_t } d W_t^V \\ d W_t^S d W_t^V & = \rho d t \end{aligned} \]

quantlib-python 中 Heston 过程的构造函数如下：

HestonProcess(riskFreeRate,
              dividendYield,
              s0,
              v0,
              kappa,
              theta,
              sigma,
              rho)

其中，

• riskFreeRate：YieldTermStructureHandle 对象，描述无风险利率的期限结构；
• dividendYield：YieldTermStructureHandle 对象，描述股息率的期限结构；
• s0：QuoteHandle 对象，资产价格的起始值；
• v0：浮点数，波动率的起始值；
• kappa、theta、sigma：浮点数，描述波动率的 SDE 的参数；
• rho：浮点数，模型中两个布朗运动之间的相关性

除了一些检查器之外，HestonProcess 没有提过其他特别的成员函数。

由于方程没有显式解，因此必须在 evolve 函数中使用算法进行离散化。quantlib-python 默认的离散化方法是 Quadratic Exponential Martingale 方法，具体的算法细节请查看参考文献（Andersen 和 Leif，2008）

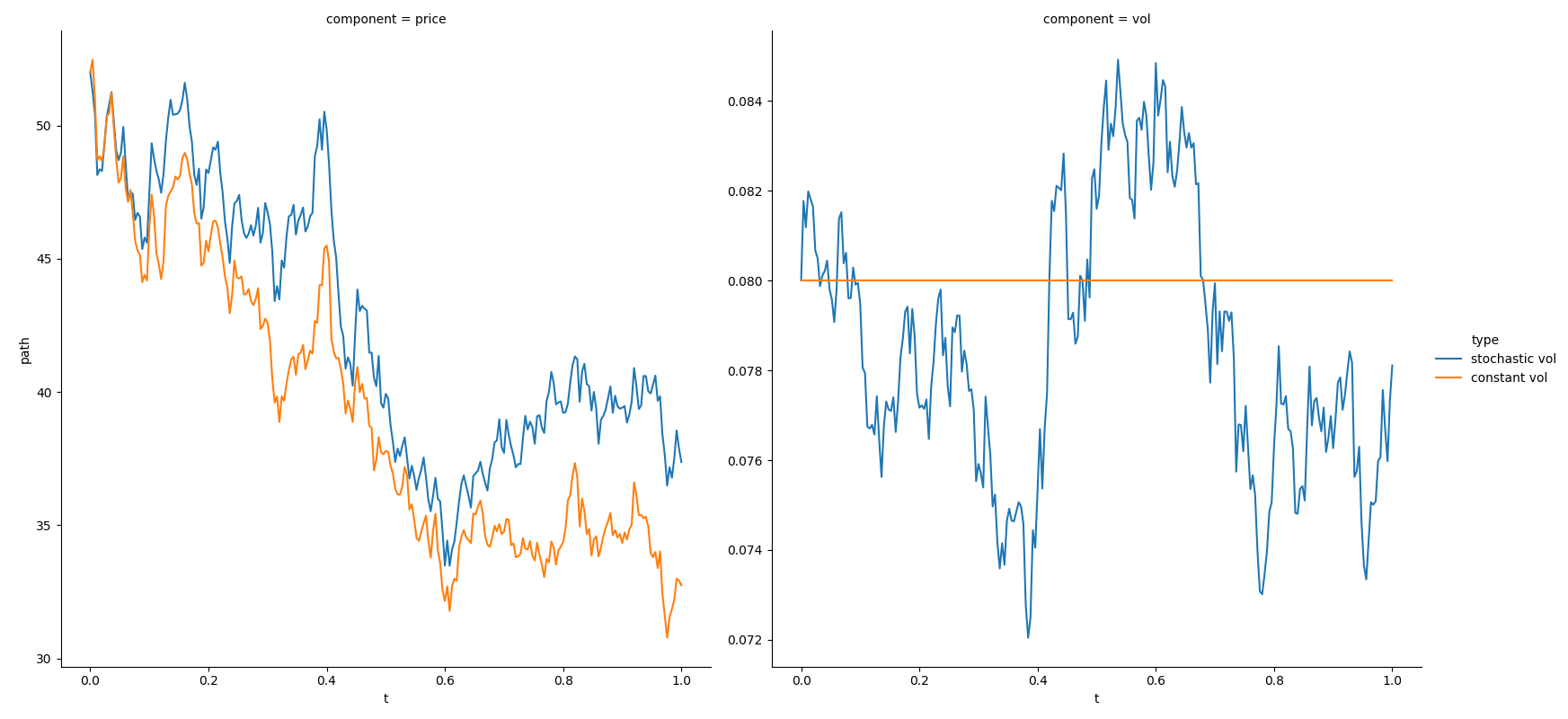
由于 evolve 函数将离散化计算中对布朗运动的离散化以参数形式暴露了出来，使得用户可以容易地显现出随机波动率对资产价格序列的影响。下面的例子比较了一般 Black Scholes 过程和 Heston 过程，所模拟的资产价格除了波动率结构以外，都完全一致。

def testingStochasticProcesses2(seed):
    refDate = ql.Date(27, ql.January, 2019)
    riskFreeRate = 0.0321
    dividendRate = 0.0128
    spot = 52.0
    cal = ql.China()
    dc = ql.ActualActual()

    rdHandle = ql.YieldTermStructureHandle(
        ql.FlatForward(refDate, riskFreeRate, dc))
    rqHandle = ql.YieldTermStructureHandle(
        ql.FlatForward(refDate, dividendRate, dc))
    spotHandle = ql.QuoteHandle(
        ql.SimpleQuote(spot))

    kappa = 1.2
    theta = 0.08
    sigma = 0.05
    rho = -0.6

    v0 = theta

    hestonProcess = ql.HestonProcess(
        rdHandle, rqHandle, spotHandle, v0,
        kappa, theta, sigma, rho)

    volHandle = ql.BlackVolTermStructureHandle(
        ql.BlackConstantVol(refDate, cal, np.sqrt(v0), dc))

    bsmProcess = ql.BlackScholesMertonProcess(
        spotHandle, rqHandle, rdHandle, volHandle)

    unifMt = ql.MersenneTwisterUniformRng(seed)
    bmGauss = ql.BoxMullerMersenneTwisterGaussianRng(unifMt)

    dt = 0.004
    numVals = 250

    dw = ql.Array(2)
    x = ql.Array(2)

    x[0] = spotHandle.value()
    x[1] = v0
    y = x[0]

    htn = pd.DataFrame(
        dict(
            t=np.linspace(0, dt * numVals, numVals + 1),
            price=np.nan,
            vol=np.nan))

    bsm = pd.DataFrame(
        dict(
            t=np.linspace(0, dt * numVals, numVals + 1),
            price=np.nan,
            vol=v0))

    htn.loc[0, 'price'] = x[0]
    htn.loc[0, 'vol'] = x[1]

    bsm.loc[0, 'price'] = y

    for j in range(1, numVals + 1):
        dw[0] = bmGauss.next().value()
        dw[1] = bmGauss.next().value()

        x = hestonProcess.evolve(htn.loc[j, 't'], x, dt, dw)
        y = bsmProcess.evolve(bsm.loc[j, 't'], y, dt, dw[0])

        htn.loc[j, 'price'] = x[0]
        htn.loc[j, 'vol'] = x[1]

        bsm.loc[j, 'price'] = y

    htn = htn.melt(
        id_vars='t',
        var_name='component',
        value_name='path')

    htn['type'] = 'stochastic vol'

    bsm = bsm.melt(
        id_vars='t',
        var_name='component',
        value_name='path')

    bsm['type'] = 'constant vol'

    htn_bsm = pd.concat([htn, bsm])

    sn.relplot(
        x='t',
        y='path',
        data=htn_bsm,
        col='component',
        hue='type',
        kind="line",
        height=8,
        facet_kws=dict(sharey=False))


testingStochasticProcesses2(100)

参考文献

• Andersen, Leif. 2008. Simple and efficient simulation of the Heston stochastic volatility model. Journal of Computational Finance 11: 1–42.

扩展阅读

《QuantLib 金融计算》系列合集