最小二乘法的原理与计算

最小二乘法的应用例子
如果某个资产在买入后，第 2-100 天内的收益变化如下图所示：

这时，我想要获得第 2-100 天内的任意收益，都是可以方便清晰获得的，但是如果我在第100天的时间，想要预估第107天时的收益呢？
从上图中，原始数据是没有第107天的收益的，这时间就必须根据2-100天的数据对第 107 天的收益进行预测。
进行预测有多种方法，但是对于上面的例子，最常见的是线性回归方式，而线性回归中最受欢迎的算法是最小二乘法。

进行线性回归后如下图所示：

红色曲线就是2-100 天的原始数据，而绿色的斜线就是线性回归线。
可以看出，绿色的线是斜率固定的，是符合函数：f(y) = b + kx，这时间就能轻松的获得第107天的预测数据。

最小二乘法的原理
我们是如何求的线性回归线呢，是又如何最小二乘法是最优的选择呢。
先看下图：

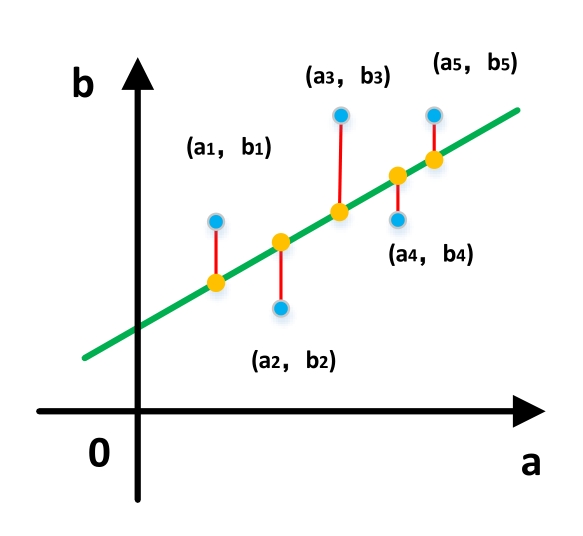
线性回归线就是蓝色的点到回归线的垂直距离和最小的直线。上图中红色的线，即真实数据到回归线的垂直距离，就是真实数据与回归线（预测数据）的误差，我们只需要使所有误差的和最小，也就是最优的。

 

利用Python代码计算最小二乘法来线性回归

x = [2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46,
47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81, 82, 83, 84, 85, 86, 87, 88, 89,
90, 91, 92, 93, 94, 95, 96, 97, 98, 99, 100]
y = [-0.19, -0.51, -0.81, -0.29, -0.9, -0.46, -0.88, -0.71, -0.14, -0.11, -0.46, -0.45, -0.13, -0.06, 0.27, 0.05, 0.23, 0.98, 0.97, 1.3, 1.04, 0.4, 0.01, 0.45, 0.38, 0.84,
0.47, 0.8, 0.17, 0.03, 0.37, 0.91, 0.71, 0.87, 1.15, 2.02, 2.22, 2.59, 3.16, 2.72, 2.78, 2.15, 3.05, 3.34, 3.39, 3.73, 3.35, 2.61, 2.59, 3.12, 3.32, 3.67, 3.23, 3.42, 3.8,
4.32, 4.98, 4.23, 4.88, 4.87, 4.59, 3.82, 3.89, 4.7, 4.89, 5.28, 4.75, 5.26, 6.55, 6.49, 7.11, 6.96, 6.74, 6.97, 6.43, 6.38, 6.36, 5.56, 5.0, 4.31, 4.23, 4.83, 5.9, 5.95,
7.21, 7.92, 7.95, 7.55, 7.32, 7.69, 8.0, 8.49, 8.75, 8.76, 8.55, 8.77, 8.76, 9.43, 9.91]
mean_x = sum(x) / len(x)
mean_y = sum(y) / len(y)
sum_x = 0.0
sum_y = 0.0
for i in range(0, len(x)):
sum_x += (x[i] - mean_x) * (y[i] - mean_y)
sum_y += (x[i] - mean_x) ** 2

k = sum_x / sum_y
b = mean_y - k * mean_x

y2 = []
# y2 对真实数据的回归
for i in range(0, len(x)):
y2.append(round(b + k*x[i], 2))

# y2 对 101 - 110 天内的预测
last_x = x[-1]
for i in range(1, 11):
x.append(last_x + i)
y2.append(round(b + k*(last_x + i), 2))

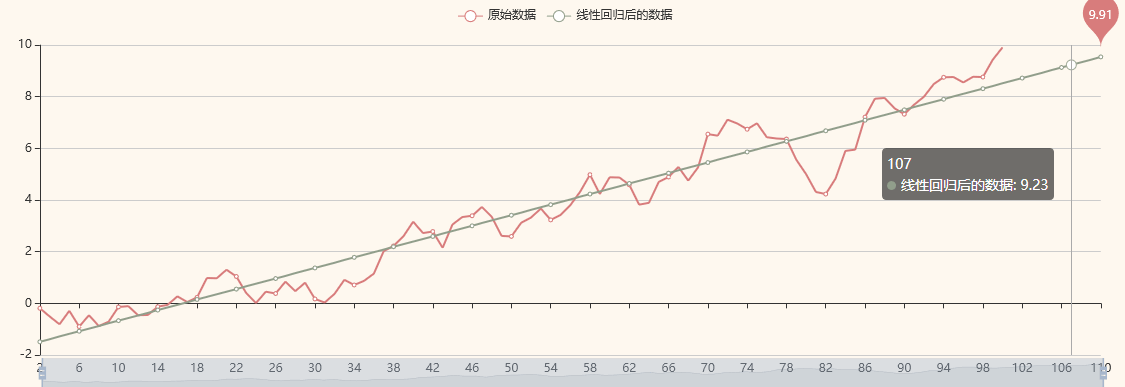
结果如图所示，预测第107天的收益是9.23：

 

本文禁止任何网站转载，严厉谴责那些蛀虫们。
本文首发于，博客园，请搜索：博客园 - 寻自己，查看原版文章