方差、标准差和协方差三者之间的定义与计算
理解三者之间的区别与联系，要从定义入手，一步步来计算，同时也要互相比较理解，这样才够深刻。
方差
方差是各个数据与平均数之差的平方的平均数。在概率论和数理统计中，方差（英文Variance）用来度量随机变量和其数学期望（即均值）之间的偏离程度。在许多实际问题中，研究随机变量和均值之间的偏离程度有着很重要的意义。
标准差
方差开根号。
协方差
在概率论和统计学中，协方差用于衡量两个变量的总体误差。而方差是协方差的一种特殊情况，即当两个变量是相同的情况。
可以通俗的理解为：两个变量在变化过程中是否同向变化？还是反方向变化？同向或反向程度如何？
你变大，同时我也变大，说明两个变量是同向变化的，这是协方差就是正的。
你变大，同时我变小，说明两个变量是反向变化的，这时协方差就是负的。
如果我是自然人，而你是太阳，那么两者没有相关关系，这时协方差是0。
从数值来看，协方差的数值越大，两个变量同向程度也就越大，反之亦然。
可以看出来，协方差代表了两个变量之间的是否同时偏离均值，和偏离的方向是相同还是相反。
公式：如果有X,Y两个变量，每个时刻的“X值与其均值之差”乘以“Y值与其均值之差”得到一个乘积，再对这每时刻的乘积求和并求出均值，即为协方差。
方差，标准差与协方差之间的联系与区别：
1. 方差和标准差都是对一组(一维)数据进行统计的，反映的是一维数组的离散程度；而协方差是对2组数据进行统计的，反映的是2组数据之间的相关性。
2. 标准差和均值的量纲（单位）是一致的，在描述一个波动范围时标准差比方差更方便。比如一个班男生的平均身高是170cm,标准差是10cm,那么方差就是10cm^2。可以进行的比较简便的描述是本班男生身高分布是170±10cm，方差就无法做到这点。
3. 方差可以看成是协方差的一种特殊情况，即2组数据完全相同。
4. 协方差只表示线性相关的方向，取值正无穷到负无穷。
利用实例来计算方差、标准差和协方差
样本数据1：沪深300指数2017年3月份的涨跌额（%）, [0.16,-0.67,-0.21,0.54,0.22,-0.15,-0.63,0.03,0.88,-0.04,0.20,0.52,-1.03,0.11,0.49,-0.47,0.35,0.80,-0.33,-0.24,-0.13,-0.82,0.56]
1. 计算沪深300指数2017年3月份的涨跌额（%）的方差
# Sample Date - SH000300 Earning in 2017-03 datas = [0.16, -0.67, -0.21, 0.54, 0.22, -0.15, -0.63, 0.03, 0.88, -0.04, 0.20, 0.52, -1.03, 0.11, 0.49, -0.47, 0.35, 0.80, -0.33, -0.24, -0.13, -0.82, 0.56] mean1 = sum(datas)/len(datas) # result = 0.0060869565217391355 square_datas = [] for i in datas: square_datas.append((i-mean1)*(i-mean1)) variance = sum(square_datas)/len(square_datas) print(str(variance)) # result = 0.25349338374291114 # 当然如果你使用了numpy，那么求方差将会十分的简单： import numpy as np datas = [0.16, -0.67, -0.21, 0.54, 0.22, -0.15, -0.63, 0.03, 0.88, -0.04, 0.20, 0.52, -1.03, 0.11, 0.49, -0.47, 0.35, 0.80, -0.33, -0.24, -0.13, -0.82, 0.56] variance = np.var(datas) print(str(variance)) # result = 0.253493383743
2. 计算沪深300指数2017年3月份的涨跌额（%）的标准差
import math # Sample Date - SH000300 Earning in 2017-03 datas = [0.16, -0.67, -0.21, 0.54, 0.22, -0.15, -0.63, 0.03, 0.88, -0.04, 0.20, 0.52, -1.03, 0.11, 0.49, -0.47, 0.35, 0.80, -0.33, -0.24, -0.13, -0.82, 0.56] mean1 = sum(datas)/len(datas) square_datas = [] for i in datas: square_datas.append((i-mean1)*(i-mean1)) variance = sum(square_datas)/len(square_datas) standard_deviation = math.sqrt(variance) print(str(standard_deviation)) # result = 0.5034812645401129 #当然如果你使用了numpy，那么求标准差将会十分的简单： import numpy as np # Sample Date - SH000300 Earning in 2017-03 datas = [0.16, -0.67, -0.21, 0.54, 0.22, -0.15, -0.63, 0.03, 0.88, -0.04, 0.20, 0.52, -1.03, 0.11, 0.49, -0.47, 0.35, 0.80, -0.33, -0.24, -0.13, -0.82, 0.56] standard_deviation2 = np.std(datas, ddof = 0) print(str(standard_deviation2)) # result =0.50348126454
请注意 ddof = 0 这个参数，这个是很重要的，只是稍后放在文末说明，因为虽然重要，但是却十分好理解。
3. 计算沪深300指数2017年3月份的涨跌额（%）与 格力电器(SZ:000651) 2017年3月份的涨跌额（%）之间的协方差
协方差是计算两组数据之间的关系，所以要引入第二个样本，即格力电器(SZ:000651) 2017年3月份的涨跌额（%）
import math # Sample Date - SH000300 Earning in 2017-03 datas_sh000300 = [0.16, -0.67, -0.21, 0.54, 0.22, -0.15, -0.63, 0.03, 0.88, -0.04, 0.20, 0.52, -1.03, 0.11, 0.49, -0.47, 0.35, 0.80, -0.33, -0.24, -0.13, -0.82, 0.56] datas_sz000651 = [0.07, -0.55, -0.04, 3.11, 0.28, -0.50, 1.10, 1.97, -0.31, -0.55, 2.06, -0.24, -1.44, 1.56, 3.69, 0.53, 2.30, 1.09, -2.63, 0.29, 1.30, -1.54, 3.19] mean_sh000300 = sum(datas_sh000300) / len(datas_sh000300) mean_sz000651 = sum(datas_sz000651) / len(datas_sz000651) temp_datas = [] for i in range(0, len(datas_sh000300)): temp_datas.append((datas_sh000300[i] - mean_sh000300) * (datas_sz000651[i] - mean_sz000651)) cov = sum(temp_datas)/len(temp_datas) print(str(cov)) # result = 0.4385294896030246 当然如果你使用了numpy，那么求协方差将会十分的简单： import numpy as np # Sample Date - SH000300 Earning in 2017-03 datas_sh000300 = [0.16, -0.67, -0.21, 0.54, 0.22, -0.15, -0.63, 0.03, 0.88, -0.04, 0.20, 0.52, -1.03, 0.11, 0.49, -0.47, 0.35, 0.80, -0.33, -0.24, -0.13, -0.82, 0.56] datas_sz000651 = [0.07, -0.55, -0.04, 3.11, 0.28, -0.50, 1.10, 1.97, -0.31, -0.55, 2.06, -0.24, -1.44, 1.56, 3.69, 0.53, 2.30, 1.09, -2.63, 0.29, 1.30, -1.54, 3.19] cov2 = np.cov(datas_sh000300, datas_sz000651, ddof=0)[1][0] print(str(cov2)) # result = 0.438529489603
请注意 ddof = 0 这个参数，这个是很重要的，只是稍后放在文末说明，因为虽然重要，但是却十分好理解。
从这个例子可以看出来，格力个股在2017年3月份是和沪深300指数正相关的，即指数涨，格力也大多是上涨的，只是 值偏小，两者之间偏离各自均值的幅度也不同，即，我们知道了2者正相关，但是不知道正相关的幅度是大是小，这个需要引入下一个名词，文章下面会介绍：相关系数。
ddof = 0 参数的说明
如果你从网上查找方差的公式，你会发现有2个公式！
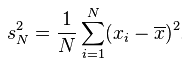和 
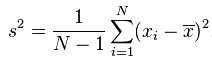
那么哪个是正确的呢？又有什么区别呢？这里就要说下贝赛尔修正：
在上面的方差公式和标准差公式中，存在一个值为N的分母，其作用为将计算得到的累积偏差进行平均，从而消除数据集大小对计算数据离散程度所产生的影响。不过，使用N所计算得到的方差及标准差只能用来表示该数据集本身(population)的离散程度；如果数据集是某个更大的研究对象的样本(sample)，那么在计算该研究对象的离散程度时，就需要对上述方差公式和标准差公式进行贝塞尔修正，将N替换为N-1：
简单的说，是除以 N 还是 除以 N-1，则要看样本是否全，比如，我要统计全国20岁男性的平均身高，这时间你肯定拿不到全部20岁男性的身高，所以只能随机抽样 500名，这时间要除以 N-1，因为只是部分数据；但是我们算沪深300在2017年3月份的涨跌幅，我们是可以全部拿到3月份的数据的，所以我们拿到的是全部数据，这时间就要除以 N。
相关系数
在我们的例子中，求的沪深300在2017年3月份的方差为0.253493383743，标准差为0.5034812645401129。
那么我们该如何理解呢？
方差：如果 股票 B 的方差是 0.1，那么我们可以说 沪深300的离散度更大，因为沪深300 的方差>股票B的方差。
标准差：沪深300的均值是：mean1 = sum(datas)/len(datas) = 0.0060869565217391355，即平均每天上涨 0.006%，那么我们描述，沪深300指数在2017年3月份平均日波动区间为[ 0.006%-0.50%， 0.006%+0.50% ]
而协方差呢，如果我只有格力和沪深300的数据，我拿到的协方差值是0.438529489603，这个值只能表明是正相关的，但是正相关的程度呢，是沪深300上涨1%，格力也上涨1%，还是沪深300上涨1%，格力涨2%呢？我们从协方差的值中无从得知。
这时间就需要另外一个变量来描述相关度的大小了：相关系数
协方差的相关系数，不仅表示线性相关的方向，还表示线性相关的程度，取值[-1,1]。也就是说，相关系数为正值，说明一个变量变大另一个变量也变大；取负值说明一个变量变大另一个变量变小，取0说明两个变量没有相关关系。同时，相关系数的绝对值越接近1，线性关系越显著。
计算公式为：就是用X、Y的协方差除以X的标准差乘以Y的标准差。
用 Python + Numpy 来实现代码如下：
import numpy as np import math # Sample Date - SH000300 Earning in 2017-03 datas_sh000300 = [0.16, -0.67, -0.21, 0.54, 0.22, -0.15, -0.63, 0.03, 0.88, -0.04, 0.20, 0.52, -1.03, 0.11, 0.49, -0.47, 0.35, 0.80, -0.33, -0.24, -0.13, -0.82, 0.56] datas_sz000651 = [0.07, -0.55, -0.04, 3.11, 0.28, -0.50, 1.10, 1.97, -0.31, -0.55, 2.06, -0.24, -1.44, 1.56, 3.69, 0.53, 2.30, 1.09, -2.63, 0.29, 1.30, -1.54, 3.19] cov = np.cov(datas_sh000300, datas_sz000651, ddof=0)[1][0] standard_deviation_sh000300 = np.std(datas_sh000300, ddof=0) standard_deviation_sz000651 = np.std(datas_sz000651, ddof=0) ppcc = cov/(standard_deviation_sh000300*standard_deviation_sz000651) print(str(ppcc)) # result = 0.554372485367
相关系数是 0.554372485367，可以看出来两者是正相关的，但是相关度很一般，至于一般的标准，就要看工作中的应用尺度了，如系数超过0.8，才存在配对交易的机会，否则，没有。
本文完，下面的文章计划介绍下协同效应的实际应用。
本文首发于，博客园，请搜索：博客园 - 寻自己，查看原版文章
