Trie 前缀树/字典树

Trie 前缀树/字典树

何为前缀树

简单来说，是一种存储字符串的数据结构。其灵魂思想可简述为不同字符串的相同字符复用。（前缀复用）

正因如此，可以节省存储空间以及查询时间。

构造前缀树

插入一个字符串 XXXXXAB (其中5个X可以为任意字符) ，我们依次插入每一个字符，假定我们现在已经将前面五个 X 插入完毕，我们现在插入字符 A , 我们要先判断以前缀 XXXXX 开头的字符串中有没有第六位为 A 的字符串，如果有，则无需插入，否则在 XXXXX 的后面插入 A 。然后我们按照相同方法插入字符 B ，不过要注意的是，B 为该字符串的最后一个字符，所以我们插入完毕后要标记该字符，方便我们之后的查找。

例如：在Trie中以此插入ABCD ABCE ABCDE BCD

1. 初始化Trie树，即一个根节点 (根节点仅仅是为了方便，看到后面查询即可理解)

2. 插入ABCD

   每一次插入都要从根节点向下找

   

3. 插入ABCE

   其中ABC在第一次插入ABCD已经插入，搜索到C时发现C下面没有E，所以插入E，并且标记为结束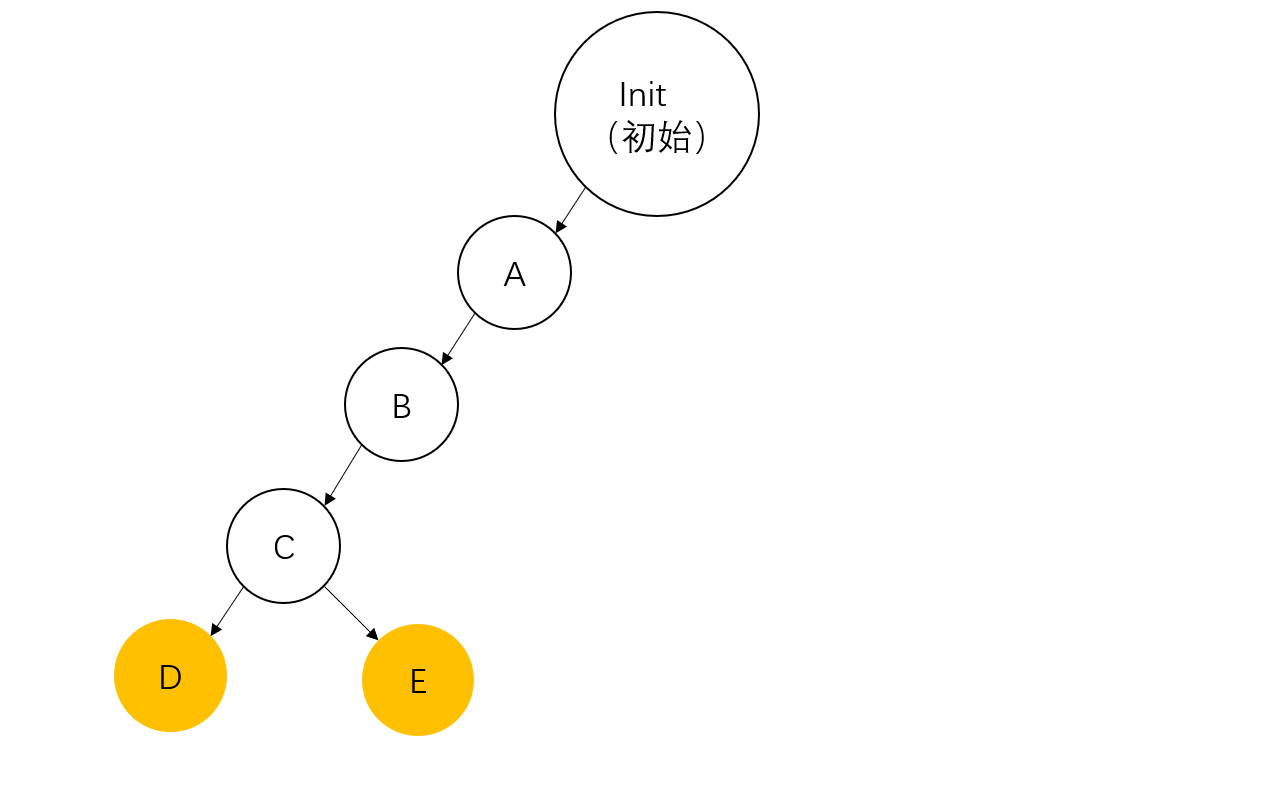

   

4. 插入ABCDE

   其中我们的标记仅仅是为了表示字符串的结束，方便我们的查询。

   所以不要认为遍历到D时就已经停止

5. 插入BCD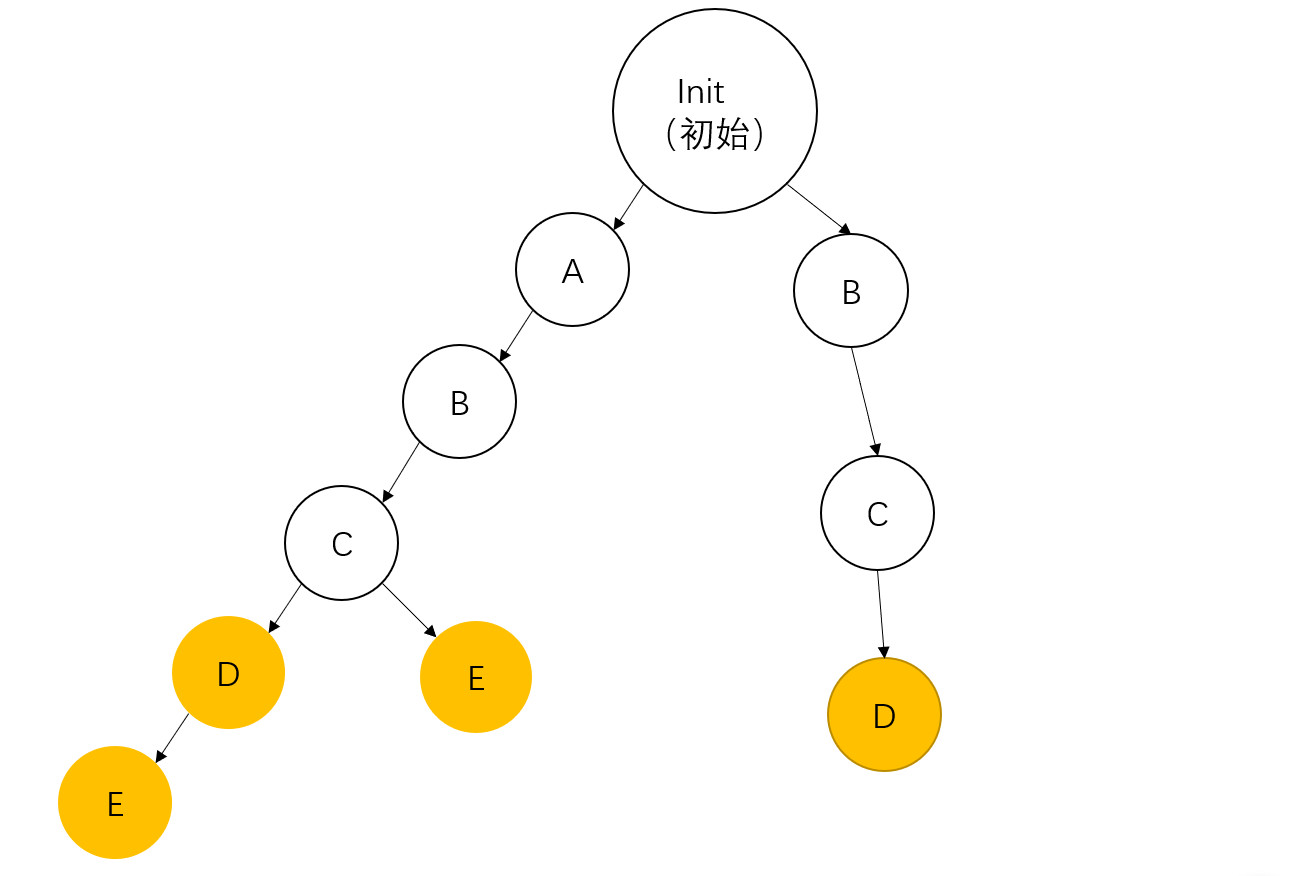

   

字符串的查询

查询很简单，从根节点开始，依次往下寻找。

以上面建好的Trie树为例：

• 例如：查询 ABCD，从根节点开始，有 A，往下找，有 B，往下找，有 C，往下找，有 D，注意这里 D 为字符串的结尾，所以我们要判断其是否被标记，其中 D 被标记，则我们在Trie树中找到了 ABCD

• 例如：查询ABD，我们从根节点开始可以依次找到 A，B，但是再往下面找不到 D 了，所以 ABD 在Trie树中不存在

• 例如：查询ABC，我们依然从根节点开始，可以找到 ABC ，但是其中 C 为字符串结尾且没有被标记，所以 ABC 在Trie树中不存在

代码实现

其根本算一种数据结构，可以建树，也可以用数组模拟树

这里给出后者的实现方法，具体注释代码中写的很详细了

---

PS: 其中难点在于trie数组的理解 画画图就好了 （抓住trie中存的是下一个点的编号这个本质就行）

// 前缀树
#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;
// 最大节点数
const int MAX_NODE = 1010;  
// 存26个字母(字符集大小)	a对应0 b对应1 ... 以此类推
const int CHARSET = 26;
// 字典树
int trie[MAX_NODE][CHARSET] = {0};
/*  trie[i][j]的值是0表示trie树中i号节点，并没有一条连出去的边，满足边上的字符标识是字符集中第j个字符（从0开始）
    trie[i][j]的值是正整数x表示trie树中i号节点，有一条连出去的边，满足边上的字符标识是字符集中第j个字符，并且这条边的终点是x号节点。
*/
int color[MAX_NODE] = {0};
// k是当前有多少节点
int k = 1;

void insert(char *w) {
    int len = strlen(w);
    int p = 0;  //Root
    for(int i = 0;i < len;i++) {
        // 0-26对应a-z
        int c = w[i] - 'a';
        // 如果没有就创建
        if(!trie[p][c]) trie[p][c] = k++;
        // p指向子节点
        p = trie[p][c];
    }
    // 最后的标记为终点
    color[p] = 1;
}
int search(char *s) {
    int len = strlen(s);
    int p = 0;
    for(int i = 0;i < len;i++) {
        int c = s[i] - 'a';
        // 如果截止了就直接没有
        if(!trie[p][c]) return 0;
        p = trie[p][c];
    }
    return color[p] == 1;
}

int main()
{
    int t,q;
    char s[20];
    cin >> t >> q;
    while(t--) {
        cin >> s;
        insert(s);
    }
    while (q--){
        cin >> s;
        if(search(s))   cout << "Yes" << endl;
        else    cout << "No" << endl;
    }
    
    return 0;
}