《线性代数》第5章相似矩阵及二次型总结

一、 向量的内积、长度、及正交性

n个数a1,a2,a3,a4,……an所组成的有序数组称为n维向量

1. 给出向量内积的定义和性质

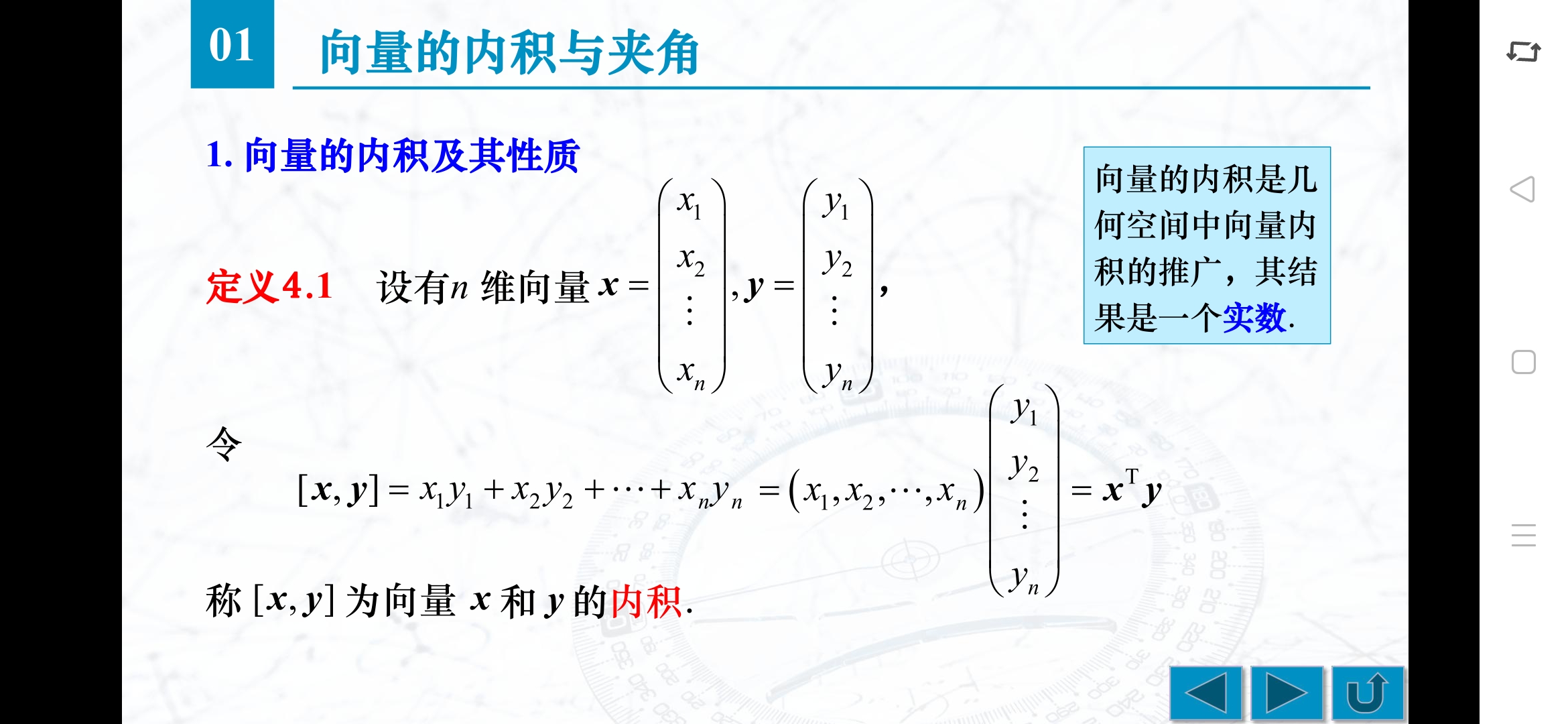
2. 向量的长度（范数）的性质

（注意柯西不等式）

3. 向量的夹角

θ的余弦值cosθ等于x与y的内积除以x范数与y范数的乘积

再看向量的正交：

就是夹角θ=90,即x向量与y向量的内积[x,y]=0

显然0向量和任何向量都正交

4. 由正交定义可以求证下列例题

因为α与β正交，所以[α,β]＝0

二、正交向量组

定义：两两正交的非零向量a1，a2，a3，……，an构成的向量组称为正交向量组

定理：正交向量组必线性无关，但线性无关的向量组未必是正交向量组

例题如下：

已知a1，a2求一个向量a3使得向量组a1，a2，a3两两正交

三、施密特正交化

定义如下

例题：将向量组规范正交化（就是先用施密特正交化方法把向量组先正交化再单位化）

已知a1求一组非零向量a2，a3使得向量组a1，a2，a3两两正交

求得基础解系:$1,$2这样得到的结果都与a1正交，但$2，$3两两之间并不正交，所有还要应用施密特公式使得$2,$3正交化

四、正交矩阵

正交矩阵的性质

例题：

写错了，是正交矩阵

五、矩阵的特征值与特征向量的求法

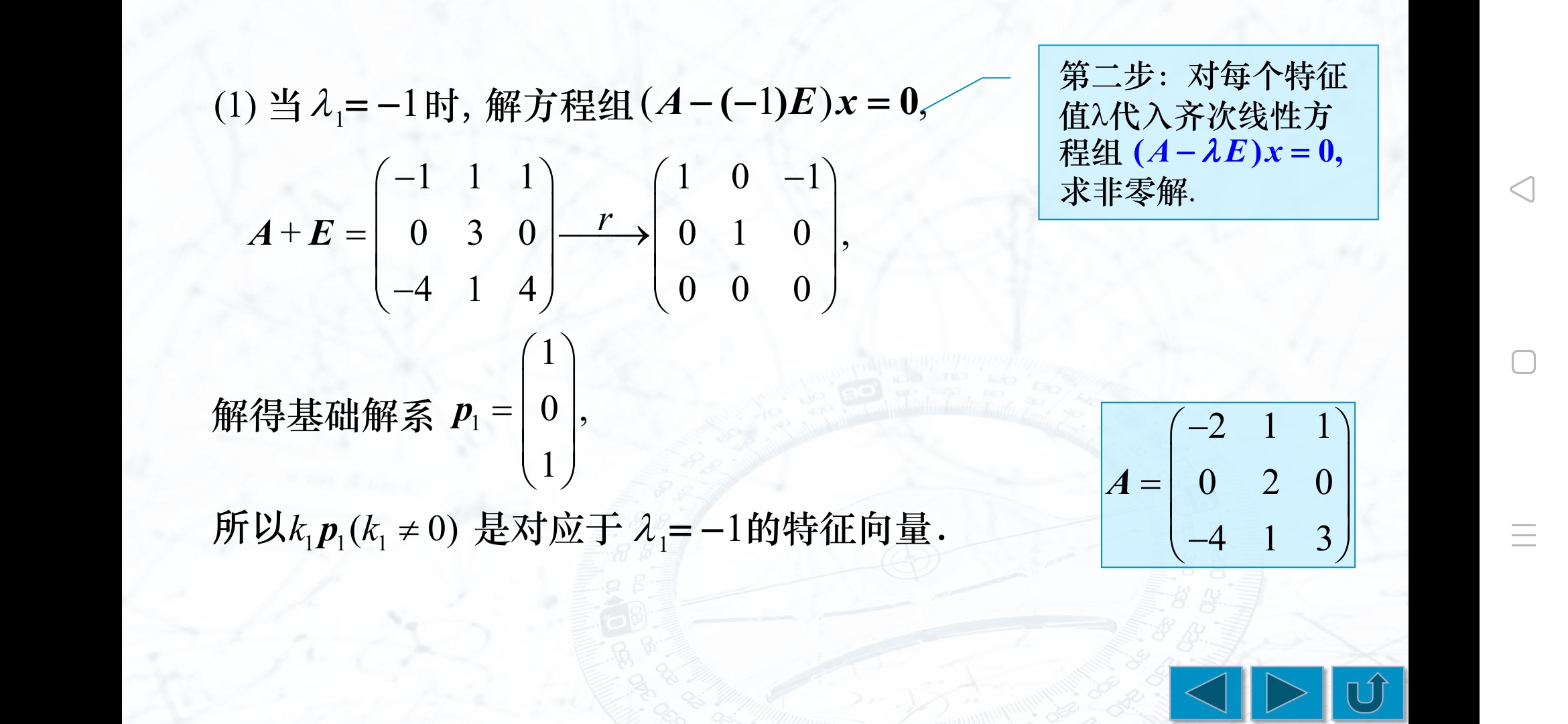
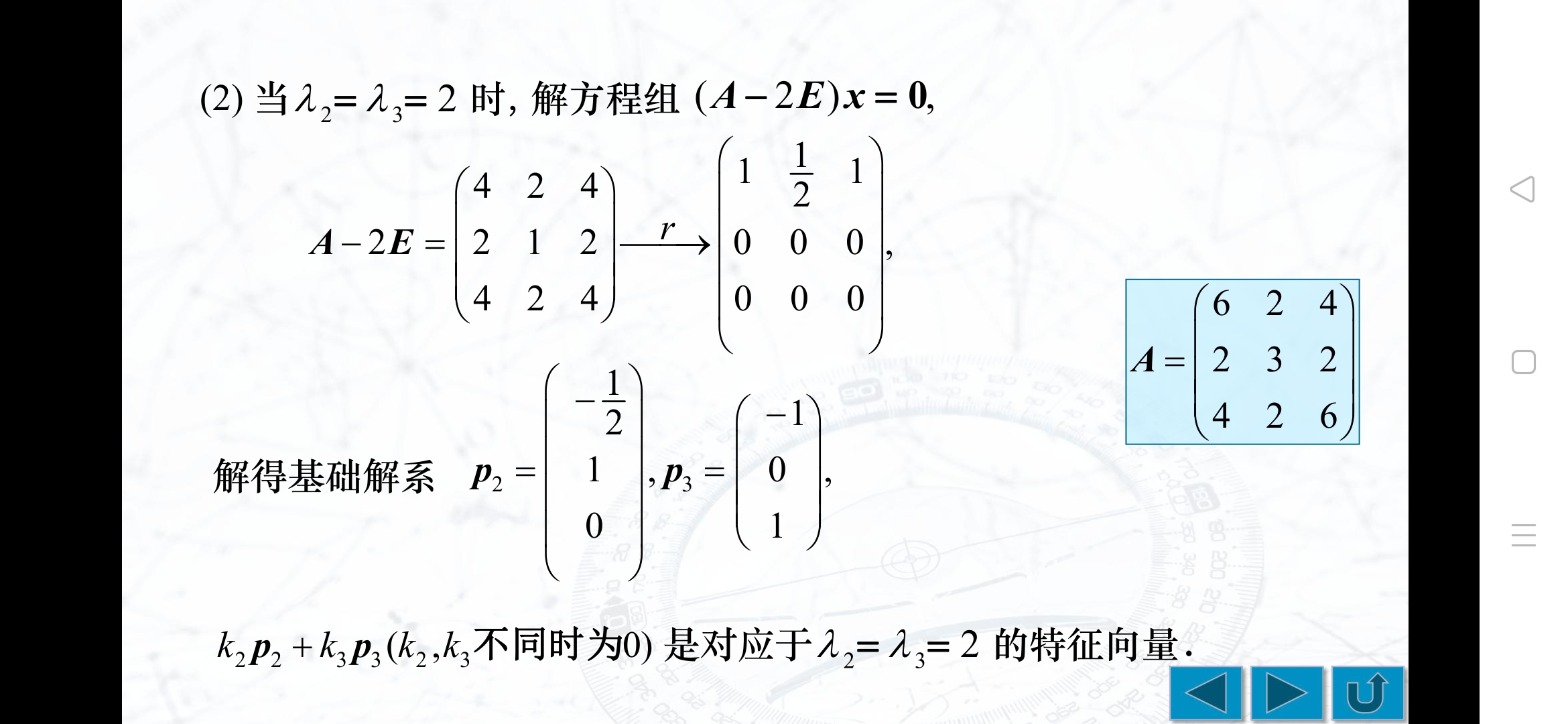
已知特征向量求行列式