同济大学《线性代数》第四章知识点-复习用
第四章 向量组的线性相关性
&1 线性方程组的解的判定
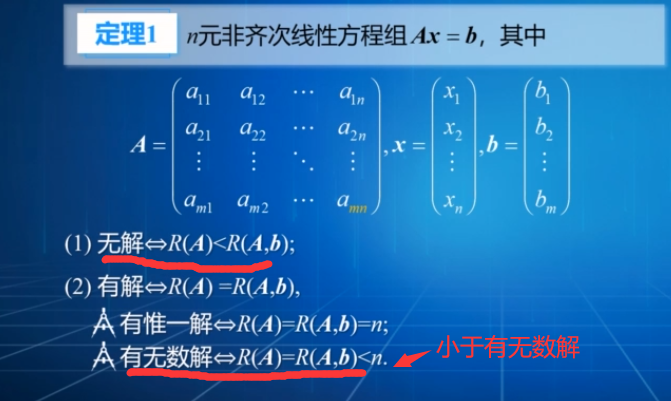
1. 对于 非齐次 线性方程组例题引入：
- 总结：
划重点：系数矩阵的 秩 要 小于 未知数的个数n 才能有无数多解
2. 对于 齐次 线性方程组
&2 线性方程组的求解
1.复习一下克拉默法则
* 定义：如果系数矩阵A的行列式不等于0，|A|！=0，那么根据克拉默法则，方程组有唯一解。
2.例题1当只有一个参数时：
3. 例题2当有2个参数时：
&3 向量组的线性表示与等价
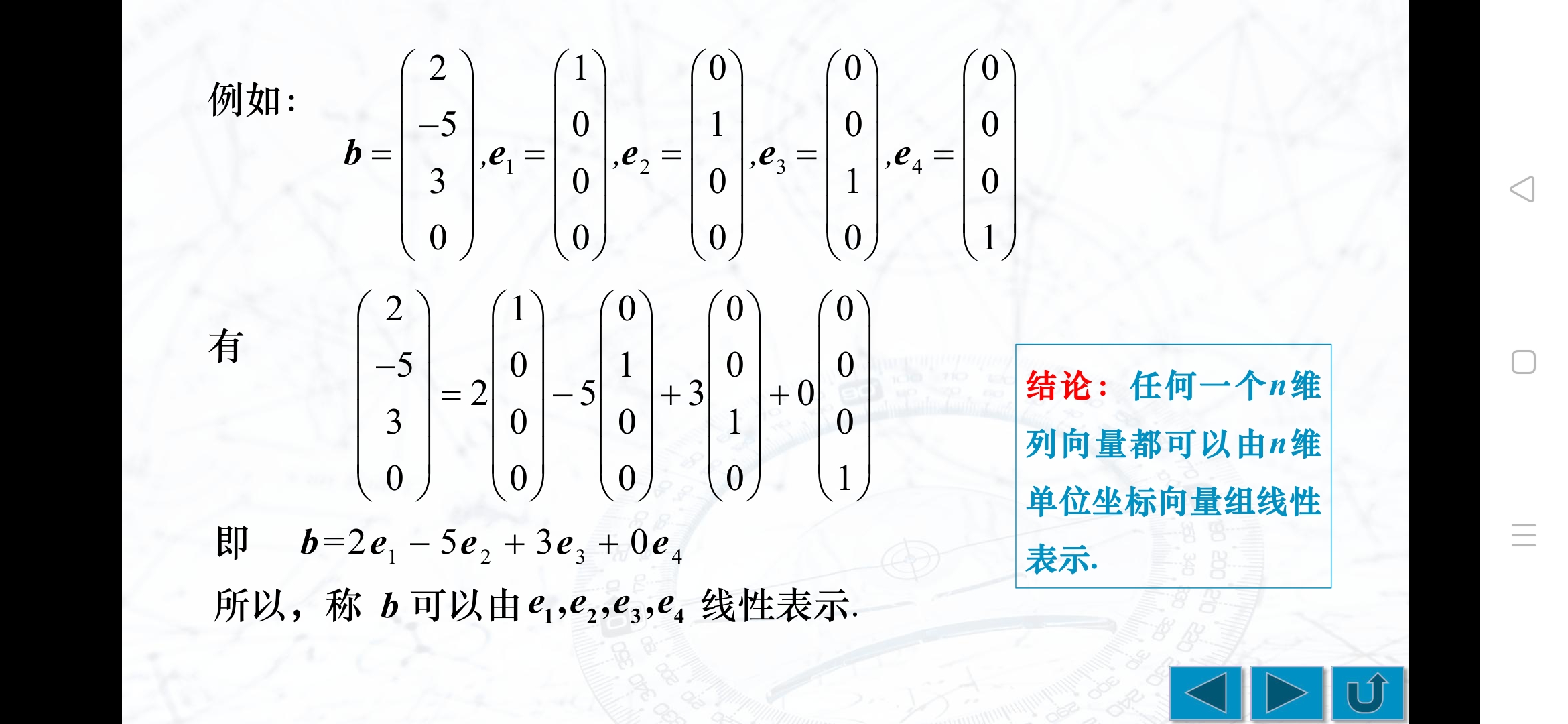
n元向量及向量组
5
10
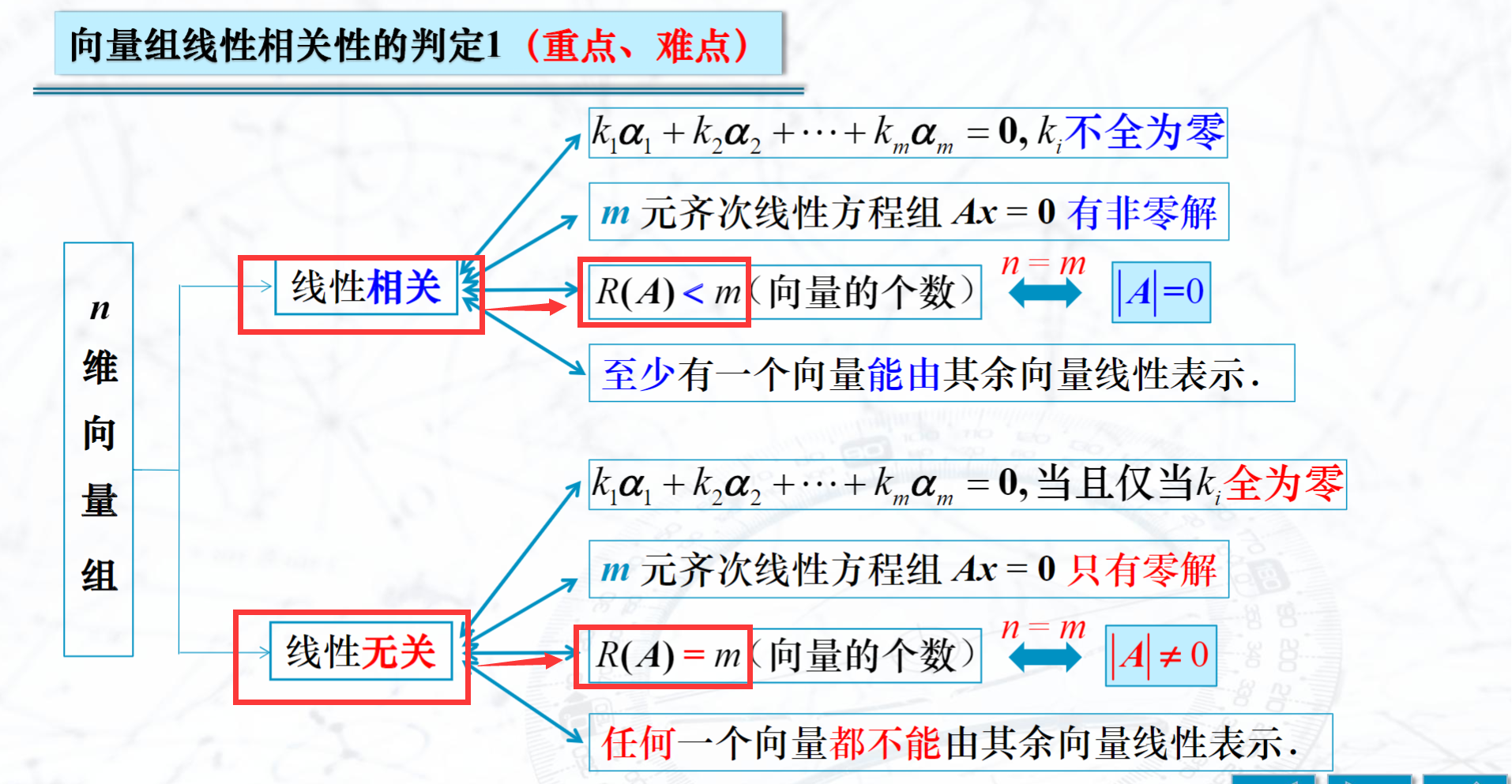
&4 向量组的秩和极大无关组
例题1：
R(A)=2原因如下图：
例题2
例题3
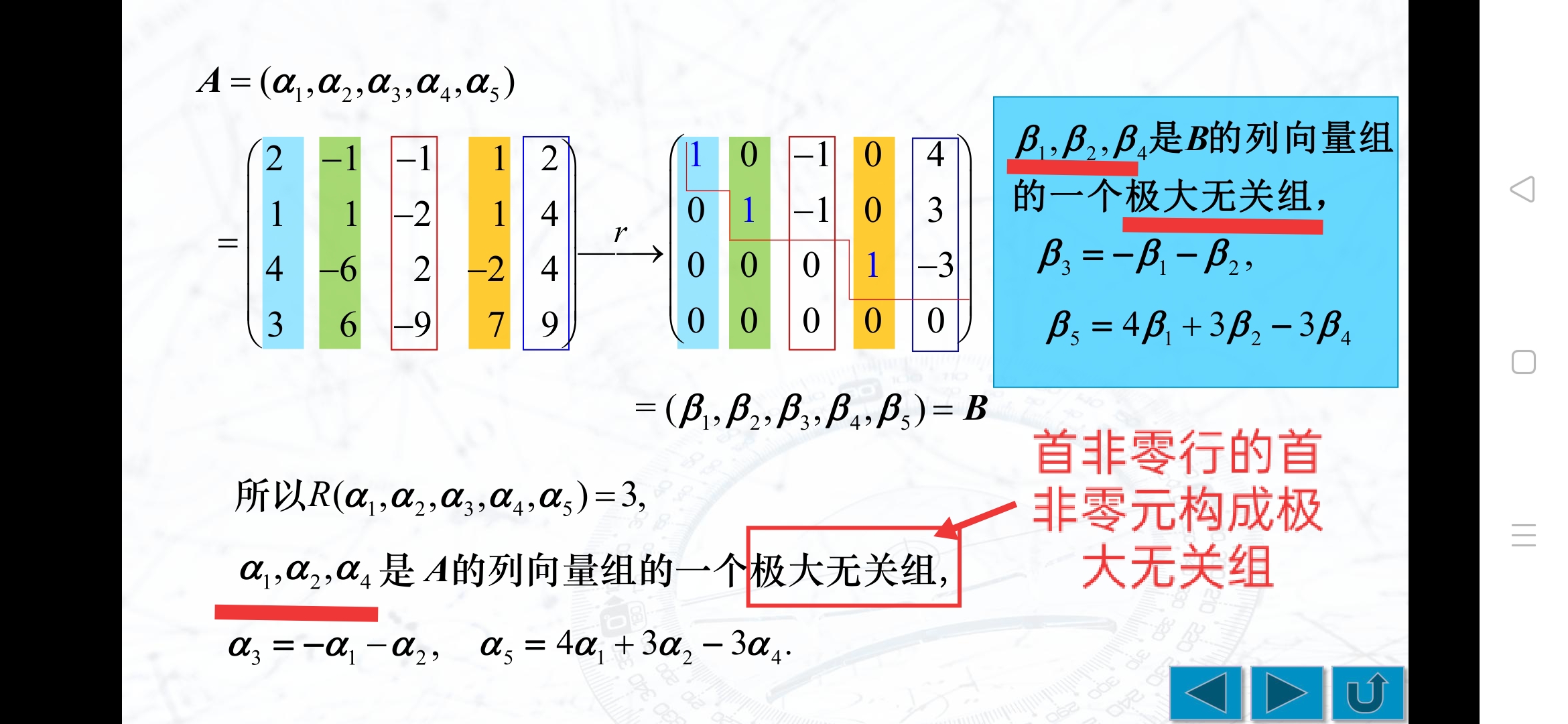
求解极大无关组，并用其表示其他向量的方法
- 由列向量组构造矩阵A
- 用初等行变换化矩阵为行最简形
- 选取行最简行矩阵中每一行首非零元所在的列向量，对应在原矩阵A中的列向量即为所求的极大无关组
&5 齐次线性方程组的解的性质
性质如下：
例题1
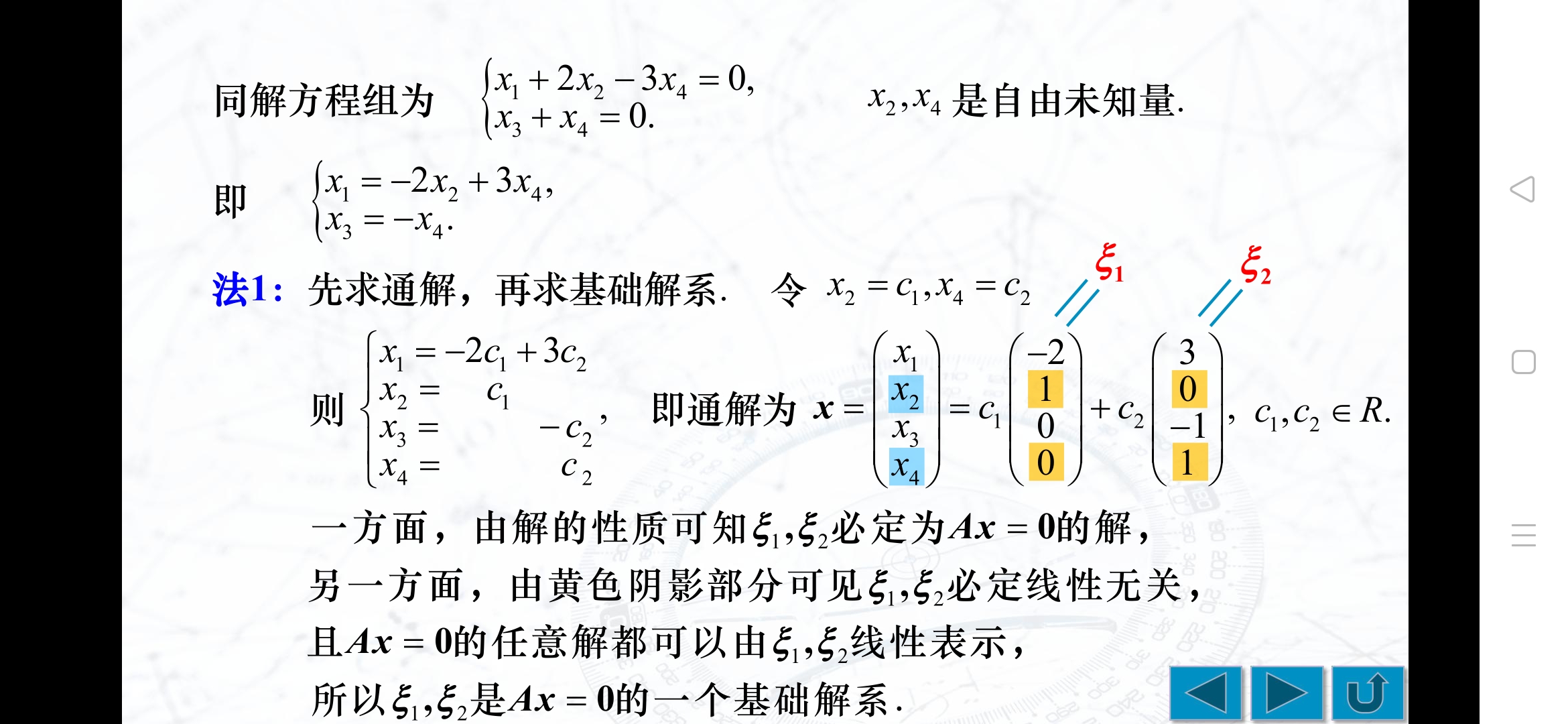
例题2
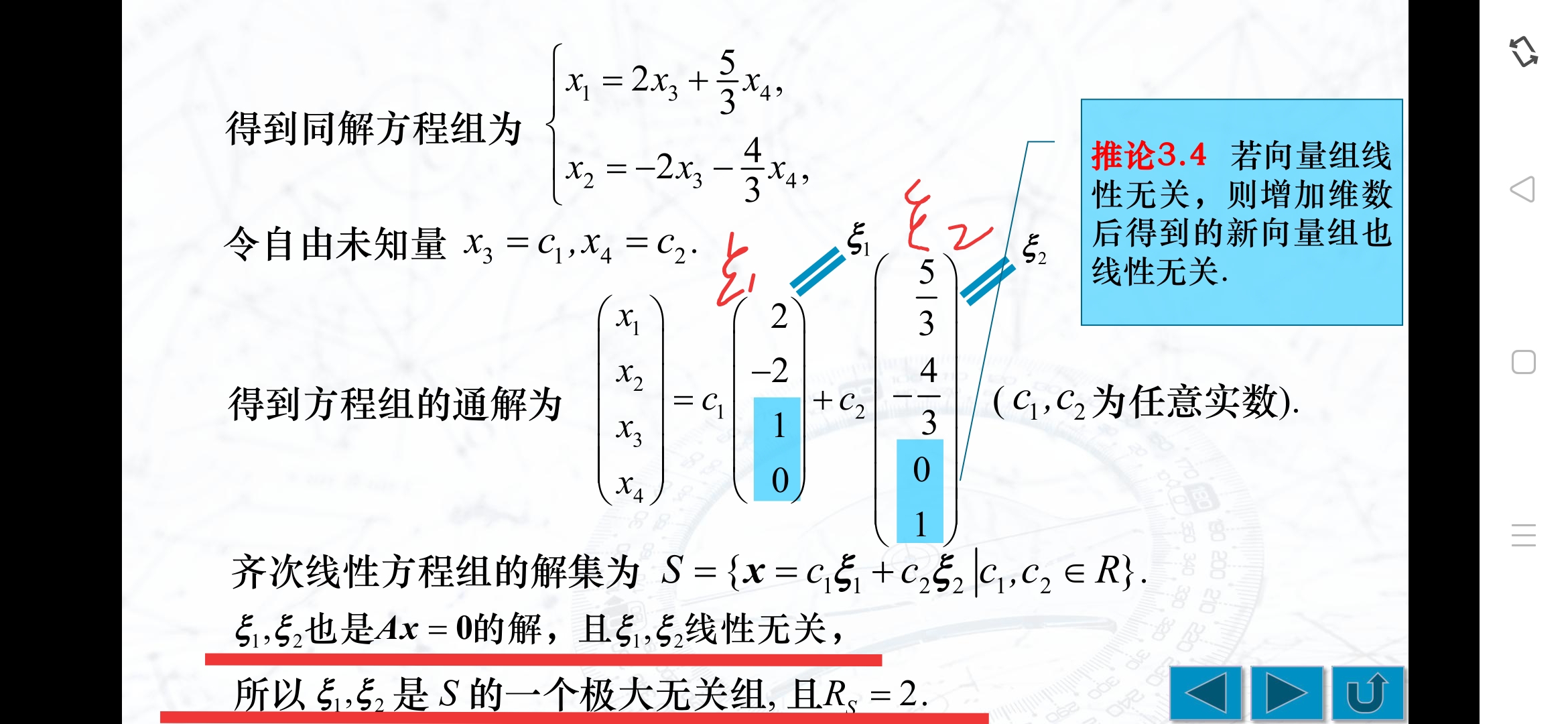
R(S) = n - R(A) ,Ax=0的全体解向量构成的集合记作S，则S为(解)向量组，R（S）的值=1，即Ax=0的任何一个非零解即为它的基础解系
所以Ax=0的通解是k1$1+k2$2,即D答案
Ax=0的基础解系中所含向量的个数（即Ax=0解集S的秩）为 n - r ,其中n是未知数的个数，r是A的秩
例题3
&6 非齐次线性方程组解的性质
&7 非齐次线性方程组的解的结构
例题1
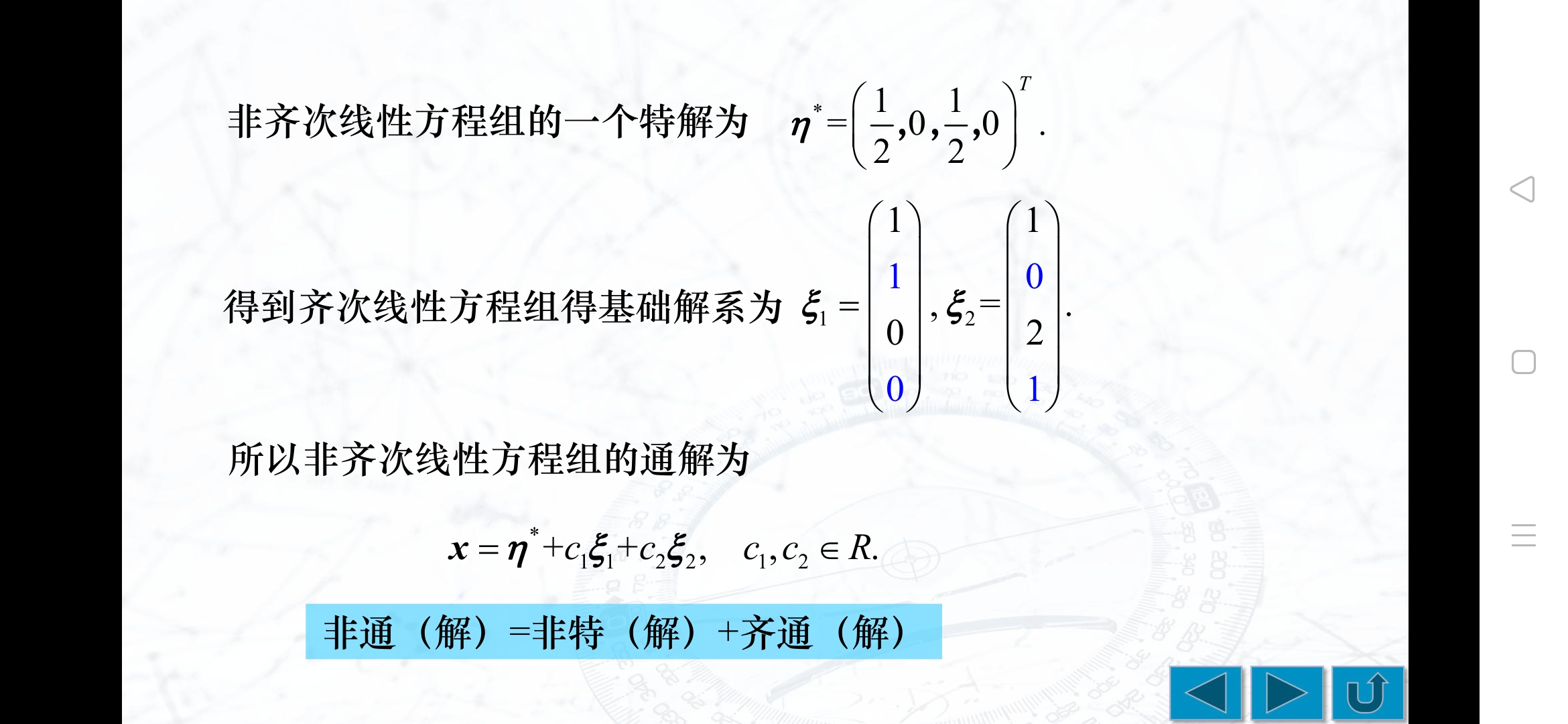
例题2
- 由性质一：n1，n2是Ax=b的解，则n1-n2是对应的齐次线性方程的解，所以本题把，n1和n2+n3化成2*n1-(n2+n3)=(n1-n2)+(n1-n3)，则该式是齐次线性方程Ax=0的解
- 由性质二：x=n是Ax=b的解，x=$是方程Ax=0的解，则x=n+$是方程Ax=b的解。
例题3
小结
例题：
