双塔召回模型问题总结

1. 常用的损失函数

一般使用inbatch softmax，主要优点是方便，缺点是容易遭造成对热门item的打压，可以做纠偏，参考youtube论文《Sampling-Bias-Corrected Neural Modeling for Large Corpus Item Recommendations》

 

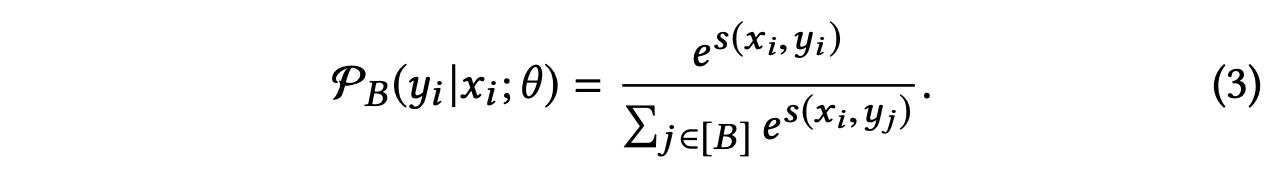
2.计算user emb 和 item emb时的相似度时应该用什么方法，为什么需要对emb做归一化？

先看一下内积、余弦相似度、欧式距离的计算公式：

内积：

\[A\cdot B={\sum_{i=1}^{n} \left ( x_{i}*y_{i}   \right ) }\]

余弦相似度：

\[\cos \left( {A,B} \right) = \frac{{A \cdot B}}{{{{\left\| A \right\|}_2}{{\left\| B \right\|}_2}}} = \frac{{\sum\limits_{i = 1}^n {\left( {{x_i} \times {y_i}} \right)} }}{{\sqrt {\sum\limits_{i = 1}^n {{{\left( {{x_i}} \right)}^2}} }  \times \sqrt {\sum\limits_{i = 1}^n {{{\left( {{y_i}} \right)}^2}} } }}\]

欧式距离：

\[dist\left( {A,B} \right) = {\left\| {A - B} \right\|_2} = \sqrt {\sum\limits_{i = 1}^n {{{\left( {{x_i} - {y_i}} \right)}^2}} } \]

如果对向量模长进行归一化，可以得到，余弦距离和内积等价，和欧式距离成反比：

\[cos\left ( A,B \right ) =A\cdot B\]

\[\left \| A-B \right \| _{2}=\sqrt{\left \|A  \right \| ^{2} +\left \|B  \right \| ^{2}-2A\cdot B}=\sqrt{2-2A\cdot B} \]

因为构建ANN索引时一般用的余弦距离（内积不满足三角不等式，效果不好），但是余弦距离的计算复杂度比较高，因此可以先对emb做归一化，然后用内积作为计算相似度的方法就可以了

 

3. 为什么需要加温度参数？

因为归一化后向量内积等于余弦相似度，值域为[-1,1]，值域太窄，加温度参数可以放大值域（因此温度参数一般是0～1之间的数）