变分自编码器VAE
生成模型如何生成样本
我们现在有一些样本(如图片),想生成更多的样本(图片),应该怎么做呢?最直接的想法是去学习样本的分布 p(X) ,从这个分布 p(X) 采样就可以了,但是真实的样本分布往往是九曲回肠的,很难通过有限的样本直接学出来
那么可以换个思路,不直接学习分布,而是学习分布的映射,即训练一个模型学习 X = g(Z)
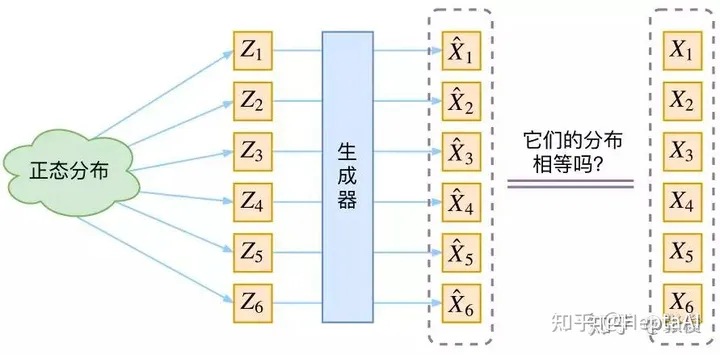
我们可以假设 Z 服从正态分布,也就是说,从正太分布中随机采样一个样本,然后通过模型把这个样本映射成目标数据,这里存在一个问题,如何判断生成的样本就是我们想要的样本呢?
最直接的方法就是计算原始样本分布和生成样本分布之间的距离,最先想到的就是KL散度,但是KL散度是计算两个已知分布的距离,现在原始样本分布 p(X) 和 生成的样本的分布 p(X') 都是未知的,无法直接用KL散度来优化
Autoencoder
在说VAE之前,先看一下传统的自编码器 (Autoencoder),Autoencoder包含了 encoder 和 decoder 两个部分结构,encoder 原始高维数据 X 映射到低维数据 Z,decoder 再把低维数据 Z 恢复成高维数据 X'
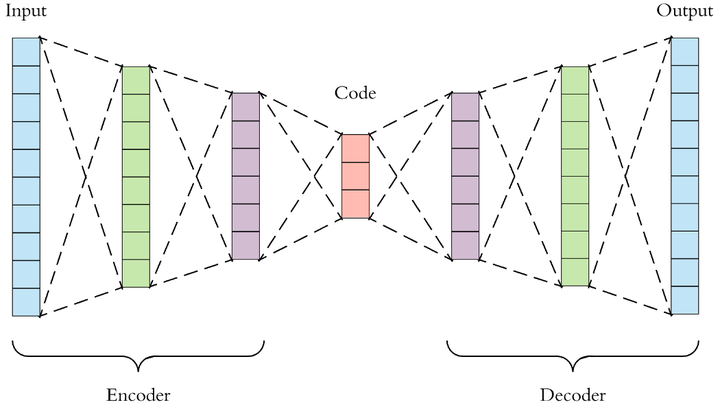
那么Autoencoder是怎训练的呢?Autoencoder 直接计算的是原始样本和生成样本的距离:
![]()
那么为什么上面提到的生成模型不可以用这个loss呢?因为我们不知道随机采样 Z 生成的样本 X‘ 和哪个真实样本对应
VAE结构初探
看一下VAE是如何解决上面的问题的,VAE把上面的过程分成两步:
1. 对每个样本X1,训练模型生成分布 p(Z1|X)
2. 从分布 p(Z1|X) 采样得到 Z1,然后训练生成器 X = g(Z) 生成 Z1 对应的 X'1
这样,p(Z1|X) 采样得到 Z1 生成的样本 X'1 必然是和 X1 对应的,那么就可以采用Autoencoder类似的loss来训练
![]()
那么如何得到p(Z1|X) 呢?VAE里假设p(Z|X) 服从正太分布,这样通过模型来拟合这个分布的均值和方差就可以得到这个分布了
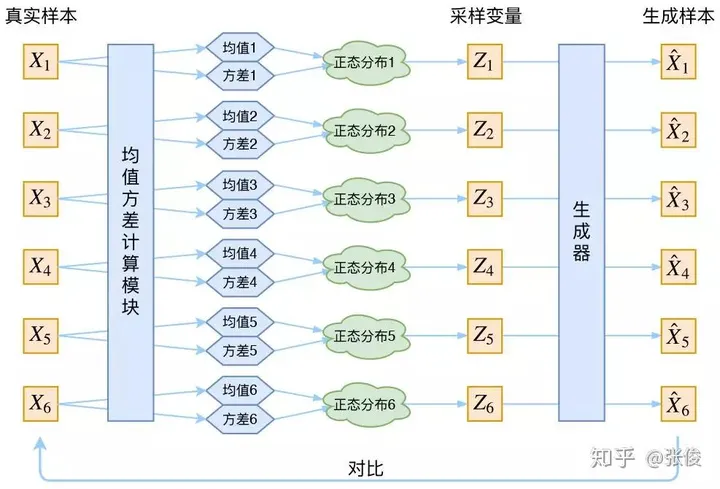
重参数技巧
现在从模型结构到loss都有了,看起来好像已经大功告成来。仔细想想,模型前向传播已经没有问题了,但是由于 Z 是通过采样得到的,采样的操作是不可导的,也就是说模型的反向传播存在问题。因此,为了让整个网络能够正常的训练,作者们提出了Reparameterization Trick,这一技巧将上述第2步改为:

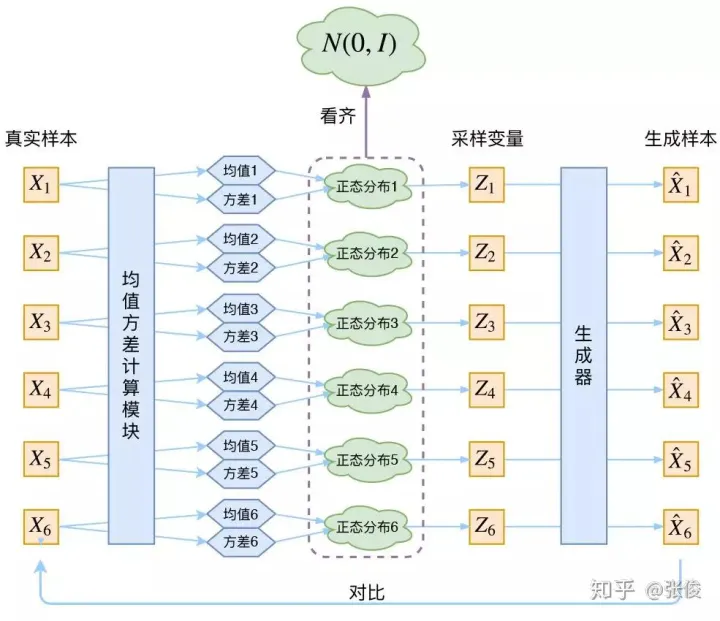
分布标准化
让我们来思考一下,根据上图的训练过程,最终会得到什么结果。首先,我们希望重构 X,也就是最小化 D(X̂k,Xk)^2,但是这个重构过程受到噪声的影响,因为Zk 是通过重新采样过的,不是直接由 encoder 算出来的。显然噪声会增加重构的难度,而且这个噪声强度(也就是方差)通过一个神经网络算出来的,所以最终模型为了重构得更好,肯定会想尽办法让方差为0。而方差为 0 的话,也就没有随机性了,所以不管怎么采样其实都只是得到确定的结果(也就是均值),只拟合一个当然比拟合多个要容易。说白了,模型会慢慢退化成普通的 AutoEncoder,噪声不再起作用。
那么如何解决这个问题呢,VAE 会强制让 p(Zk|Xk) 都向标准正态分布看齐,这样就防止了噪声为零。并且还可以推导出 p(Z) 也服从标准正态分布:
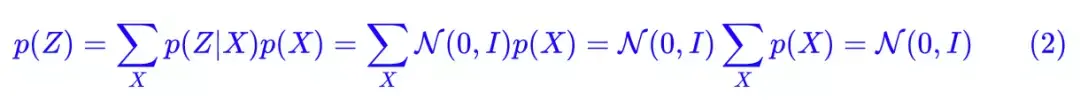
那么如何让 p(Zk|Xk) 都向标准正态分布看齐,最小化p(Zk|Xk) 和标准正太分布的交叉熵就可以了
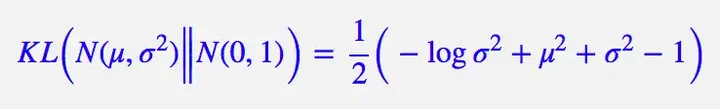
最终的loss函数
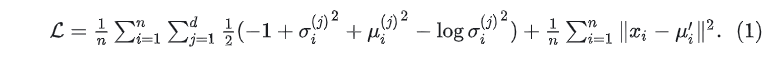
参考实现
https://github.com/siqim/Machine-Learning-with-Graphs/blob/main/examples/MLMath/VAE.py
参考资料
https://zhuanlan.zhihu.com/p/525106459






【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· TypeScript + Deepseek 打造卜卦网站:技术与玄学的结合
· 阿里巴巴 QwQ-32B真的超越了 DeepSeek R-1吗?
· 【译】Visual Studio 中新的强大生产力特性
· 10年+ .NET Coder 心语 ── 封装的思维:从隐藏、稳定开始理解其本质意义
· 【设计模式】告别冗长if-else语句:使用策略模式优化代码结构