Uplift Model介绍
背景
CTR、CVR模型建模的是预估看过广告之后的点击率和转化率,称为响应模型(response model),建模的是相关性,但是缺点是没法区分这个点击转化中有多少是广告带来
Uplift Model是估计用户因为广告而购买的概率,这是一个因果推断的问题,建模的是营销带来的增量
Reponse model: P(Y = 1 ∣ X) ,看过广告之后购买的概率
Uplift model: P(Y = 1 ∣ X , T) ,因为广告而购买的概率,其中T表示干预策略(如是否推送广告)
Uplift Model建模
Uplift Model的建模目标是:P(Y | X, T = 1) - P(Y | X, T = 0),即建模营销带来的增量
Uplift Model建模有以下几个难点:
1. 获取到的训练数据是不完整的,对于个体来说,我们不可能同时观测到在有干预和没有干预两种情况下的表现,也就是因果推断中经常提到的反事实的问题。我们应当如何去建模呢?可以换一种思路,从人群的角度来对平均因果效应做统计,假设我们有两群同质用户,均来自一线城市/年龄段为25-35/女性,我们可以对其中一组用户进行广告投放,另外一组不进行任何干预,之后统计这两群人在转化率上的差值,这个差值可以被近似认为是具备同样特征的人可能的平均因果效应。所以Uplift Model本质是从训练样本中学习条件的平均因果效应,同时因为模型是具有一定的泛化能力,可以对没有见过的样本也进行预测。
2. Uplift建模对样本的要求是比较高的,需要服从CIA ( Conditional Independence Assumption ) 条件独立假设,要求X与T是相互独立的。什么样的样本有这样的特征,又如何获取呢?最简单的方式就是随机化实验A/B Test,因为通过A/B Test拆分流量得到的这两组样本在特征的分布上面是一致的,也就是X和T是相互独立的。因此随机化实验是Uplift Model建模过程中非常重要的基础设施,可以为Uplift Model提供无偏的样本
差分响应模型(Two-Model Approach)
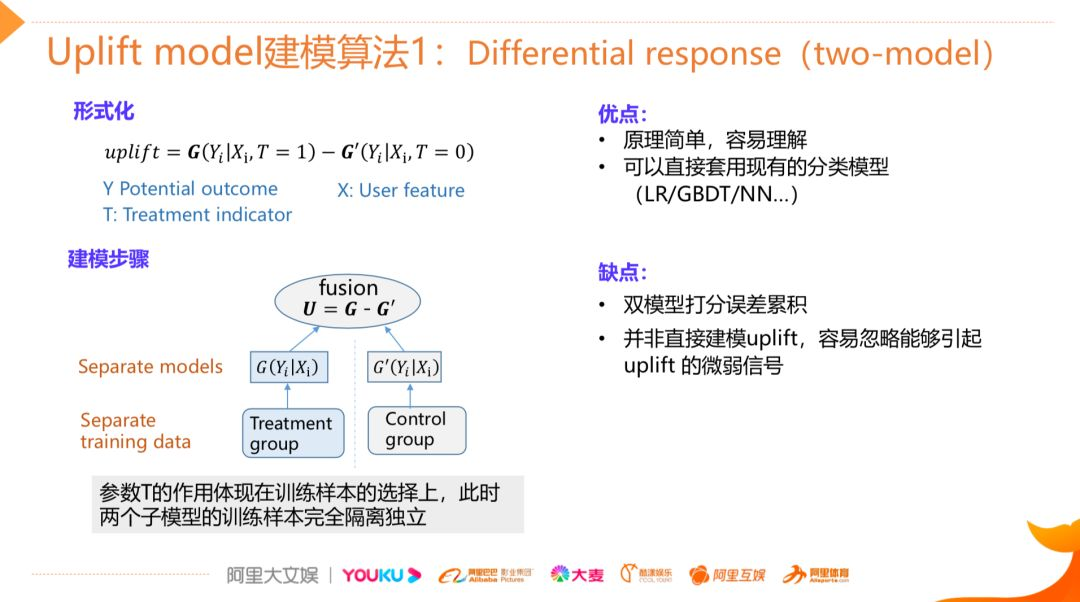
包含了两个响应模型,其中一个模型G用来估计用户在有干预情况下的响应,另外一个模型G'是用来学习用户在没有干预情况下的响应,之后将两个模型的输出做差,就得到我们想要的uplift。这种建模方法的优点是比较简单容易理解,同时它可以套用我们常见的机器学习模型,如LR,GBDT,NN等,所以该模型的落地成本是比较低的,但是该模型最大的缺点是精度有限,这一方面是因为我们独立的构建了两个模型,这两个模型在打分上面的误差容易产生累积效应,第二是我们建模的目标其实是response而不是uplift,因此对uplift的识别能力比较有限。
差分响应模型升级版(One-Model Approach)

进一步地,还有一个基于One Model的差分响应模型,它和上一个模型最大差别点在于,它在模型层面做了打通,同时底层的样本也是共享的,之所以能实现这种模型层面的打通,是因为我们在样本的维度上做了一个扩展,除了user feature之外,还引入了与treatment相关的变量T ( T如果是0,1的取值可以建模single treatment,T也可以扩展为0到N,建模multiple treatment,比如不同红包的面额,或者不同广告的素材 ),One Model版本和Two Model版本相比最大的优点是训练样本的共享可以使模型学习的更加充分,同时通过模型的学习也可以有效的避免双模型打分误差累积的问题,另外一个优点是从模型的层面可以支持multiple treatment的建模,具有比较强的实用性。同时和Two Model版本类似,它的缺点依然是其在本质上还是在对response建模,因此对uplift的建模还是比较间接,有一定提升的空间。
Modeling Uplift Directly

所以后续也有相关研究提出了第三种建模方法,通过对现有的模型内部进行深层次的改造来直接刻画uplift,其中研究较多的是基于树模型的uplift建模,下面主要介绍它的思想,在传统的决策树构建中,最重要的环节是分裂特征的选择,我们常用的指标是信息增益或者信息增益比,其背后的含义还是希望通过特征分裂之后下游节点的正负样本的分布能够更加的悬殊,也就代表类的纯度变得更高。类似的,这种思想也可以引入到Uplift Model的建模过程中,虽然我们并没有用户个体的uplift直接的label,但是我们可以通过treatment组和control组转化率的差异来刻画这个uplift,以图中左下角的图为例,我们有T和C两组样本,绿色的样本代表正样本,红色的代表负样本,可以看到在分裂之前T和C两组正负样本的比例比较接近,但是经过一轮特征分裂之后,T和C组内正负样本的比例发生了较大的变化,左子树中T组全是正样本,C组全是负样本,右子树正好相反,C组的正样本居多,意味着左子树的uplift比右子树的uplift更高,即该特征能够很好的把uplift更高和更低的两群人做一个区分。如何从数学上度量这种概率分布的差异的方式呢?一些文章提出了可行的方法,比如基于KL散度,欧式距离,卡方距离的等等。这种模型的优点是可以直接对uplift进行建模,因此它的精度理论上是更高的,但是在应用层面我们需要做大量的改造和优化,除了前面介绍的分裂规则之外,我们还需要改造它的loss函数,后续的剪枝等一系列的过程,所以它的实现成本是比较高的。
Uplift Model建模评估
难点:没有单个用户uplift的ground truth,因此传统的评估指标像AUC是无法直接使用的
AUUC
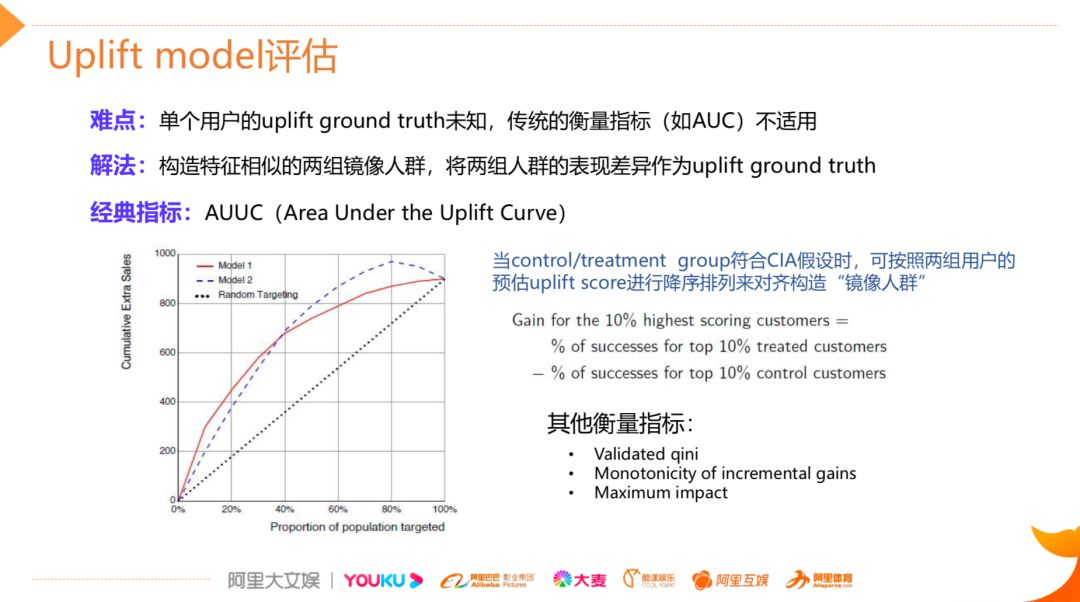
1. 将训练好的模型分别预测实验组和对照组的测试集数据,得到这两群人的 uplift score,然后按照 uplift score 进行降序排列
2. 分别截取 top10%,top20% … top100% 的用户,计算每一分位下两组人群的转化率差异,这个差异可以近似地认为是该分位下对应人群的真实 uplift 值,将这些分位差异值连接起来就得到 uplift curve ,其具体计算公式如下:
其中,$\phi$是按照 uplift score 由高到低排序的用户数量占实验组或对照组用户数量的比例,比如 $\phi=0.1$表示实验组或者对照组 top10% 的用户。$n_{t,y=1}(\phi)$表示在$\phi$下,实验组中转化(下单)的用户数;同理$n_{c,y=1}(\phi)$表示在同样分位数下,对照组中转化的用户数。






