延迟转化建模《Modeling Delayed Feedback in Display Advertising》论文阅读
背景
在计算广告的CVR预估中存在正例回传延迟的问题,具体来说就是用户的一个click行为可能要过好几天才知道会不会发生convert(这和广告的归因逻辑有关,一般会把convert归因给n天内最后发生click的事件)。这样导致了模型训练时不知道一个样本是不是真的负样本。
其中一个朴素的解决方法时等待一个固定的时间窗口,超过这个时间窗口还没回传转化的样本都看作负样本,但是这样做的缺点是:如果时间窗口设的太短会丢失大量的正例,时间窗口设的太长模型的时效性有损。
这篇论文通过引入一个用于捕捉转化延迟的额外模型来解决这个问题。直观地讲,这个概率模型帮忙决定一个还没有回传转化的样本是应该被当做负例,还是当做未知样本不参与训练:若现在转化还没有回传,现在距离click发生的时间间隔比预估的延迟时间大,则当做负例,否则当做未知样本
建模
首先定义要用到的符号的意义:

主要的逻辑关系:
![]()
![]()
![]()
等式2表示一个点击目前没有观察到发生转化等价于这个点击最终不会发生转化或目前经过的时间小于这个转化的延迟时间
等式3表示已经观察到这个时间发生转化了,那么这个事件最后一定会发生转化
等式4假设了一个click最终是否会发生转化以及转化回传的延迟时间只和特征有关和经过的时间无关
论文建模了两个模型:
1. 用于预测一个样本最终是否会发生转化的LR模型(建模 Pr(C | X)):

2. 预测转化延迟时长的指数分布模型(建模 Pr(D | X,C = 1),这里假设了正样本的回传时长服从指数分布)
![]()
![]()
一个转化延迟为di且被观察到为正样本的概率为:

一个样本被观察到为负样本的概率为:
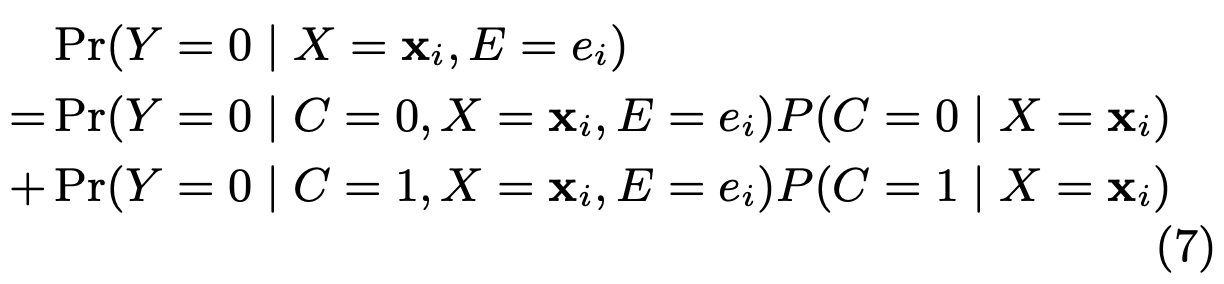
由于:
![]()
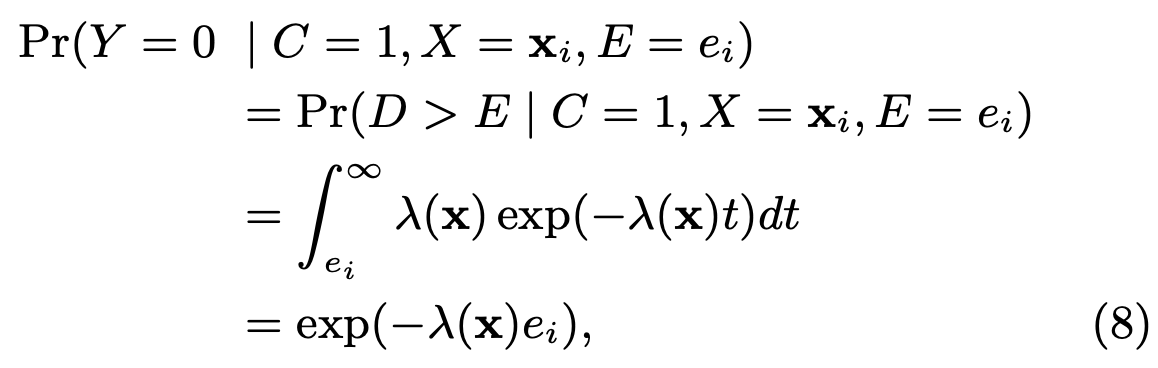
所以:
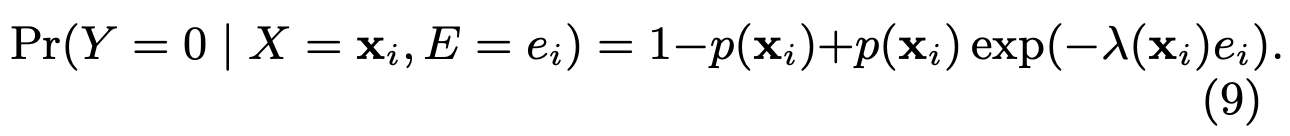
优化
论文中提出了两种优化方法,一是用EM算法,推理出来隐藏变量C(用户是否发生转化),从而解出来两个模型。二是直接用梯度下降法来优化对数似然函数
EM算法
EM算法常常用来求解带有隐变量的最大似然估计问题,这个问题中的C正是隐变量
Expectation step
对于给定的观察数据(xi, yi, ei),先计算Q函数的分布,也就是隐变量的后验分布,标记:
![]()
如果yi=1,那么wi=1
如果yi=0,那么:

Maximization step
E步得到隐变量的后验分布后,在M步需要计算观测数据的最大似然估计,现在观测数据的对数似然函数可以写为:

根据等式8,可以对等式12的第二部分做如下推导:
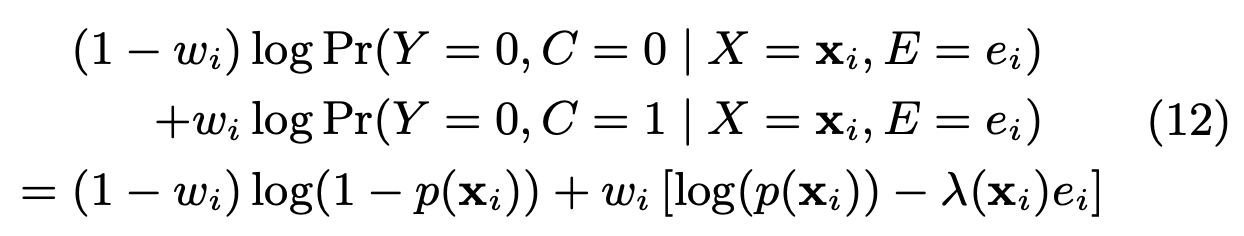
把等式6和等式12代入到等式11,可以得到最终的似然函数:
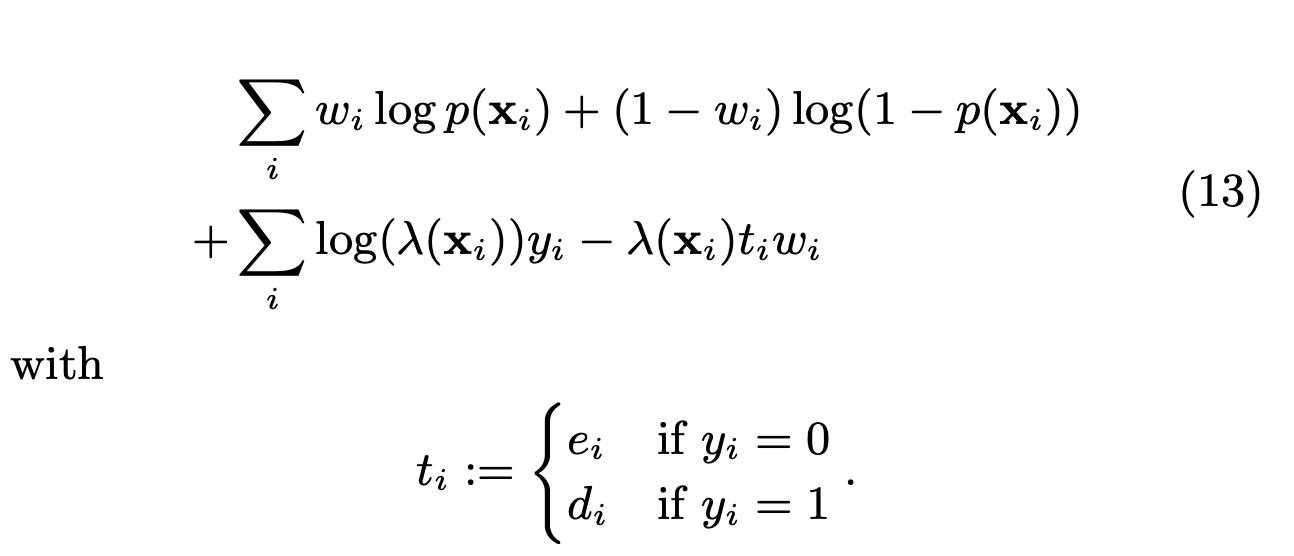
等式13具有以下几个性质:
1. p和λ是分开的,可以独立优化,且都是凸优化
2. 容易理解
EM算法的缺点是EM算法是一个嵌套优化问题,收敛比较慢
联合优化
第二种方法就是对观测到的样本,利用最大似然估计法直接优化转化率预估模型 P 和时间模型 λ 的参数。
论文中的实验都是用这个方法作为优化方法的
首先,Loss函数可以用下面这个式子来表达:
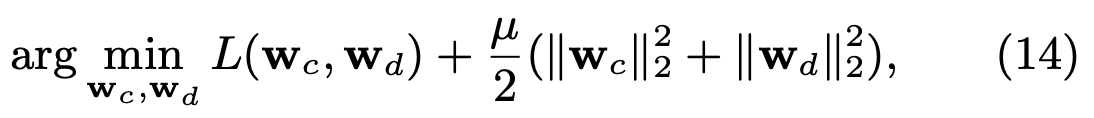
根据等6和等式9,可以得到:

注意,这个Loss是非凸的,非凸的原因直观理解就是一个还没回传转化的样本,不知道是由于这个样本最终不会发生转化还是发生点击后经过的时间太短导致的,但是作者在实验时没法发现陷入局部最后点的情况。
是用链式法则可以很容易得到参数的梯度:
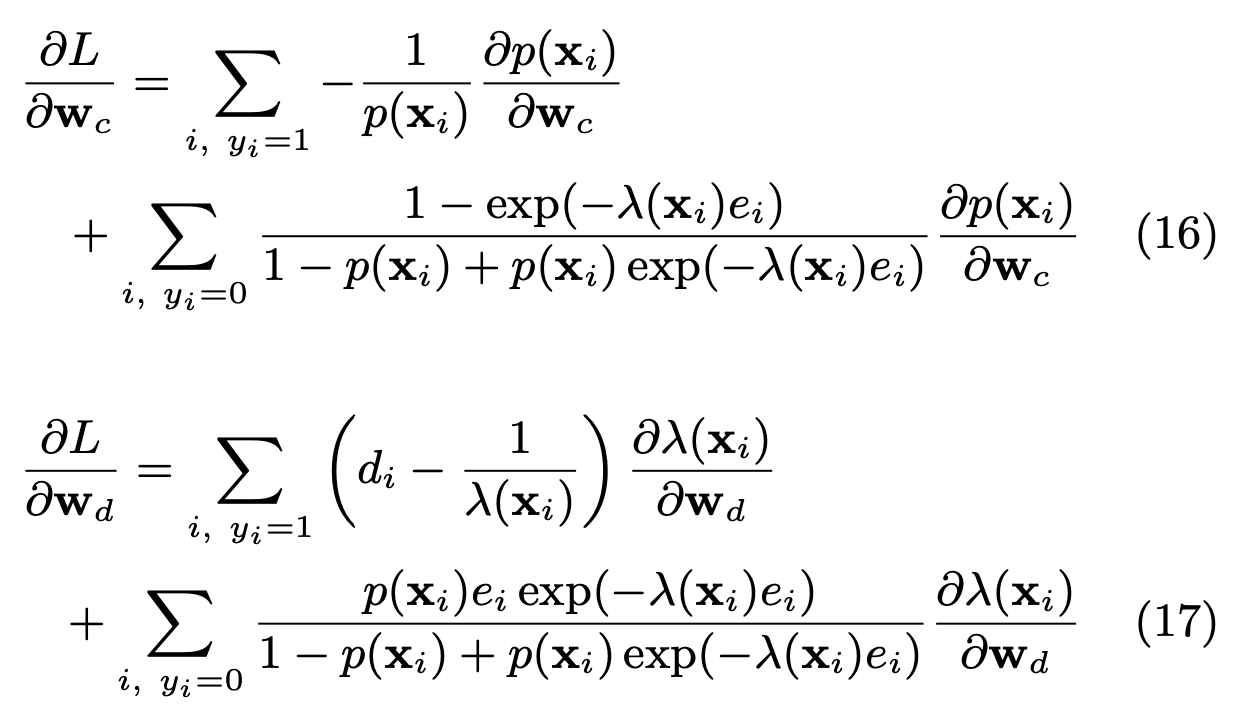
为了看出时间分布延迟模型对转化模型参数更新时的影响,这里给出不考虑验本回传延迟时的建模:
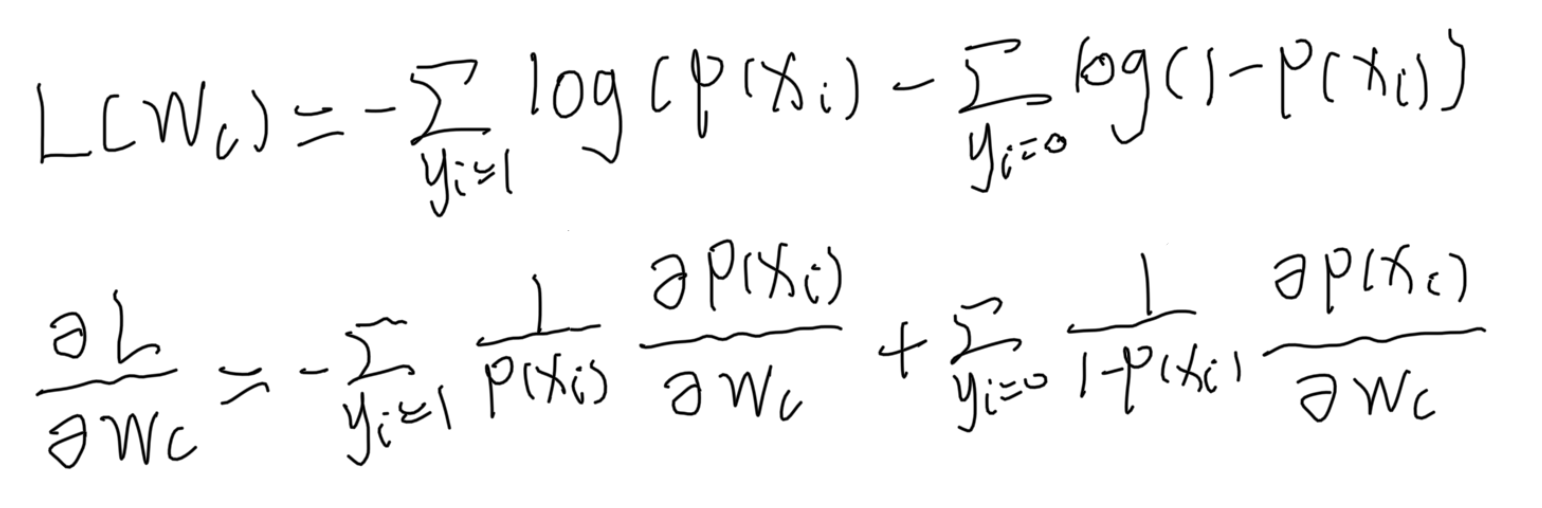
可以看出只是没有回传转化的样本,时间分布模型才会影响转化率模型参数的更新,进一步分析:
1. 当 ei « λ(xi)-1 时(指数分布的均值是λ-1)
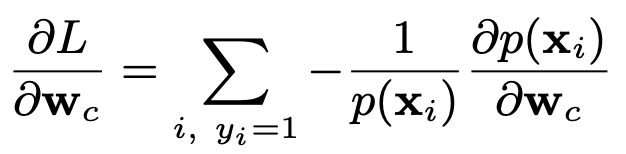
也就是说,当一个click发生后经过的时长远小于这类样本转化回传延迟的均值时,这类样本几乎不会对转化模型的更新产生影响(因为这类样本几乎无法判断是否会发生转化)
2. 当 ei » λ(xi)-1 时

也就是说,当一个click发生后经过的时长远大于这类样本转化回传延迟的均值时,和不考虑回传延迟建模时参数的更新一样,因为这类样本就可以被认为是负样本




