最小生成树

最小生成树概念

一个无向连通图G的最小生成树就是由该图的那些连接了G的所有顶点的边构成的树，且其总权重最低。最小生成树存在当且仅当G是连通的。

 

prim算法（普里姆算法）

算法思想：

prim算法是一种贪心算法，每次在未选节点中贪心的选取与已选节点中距离最近的一个节点。

 

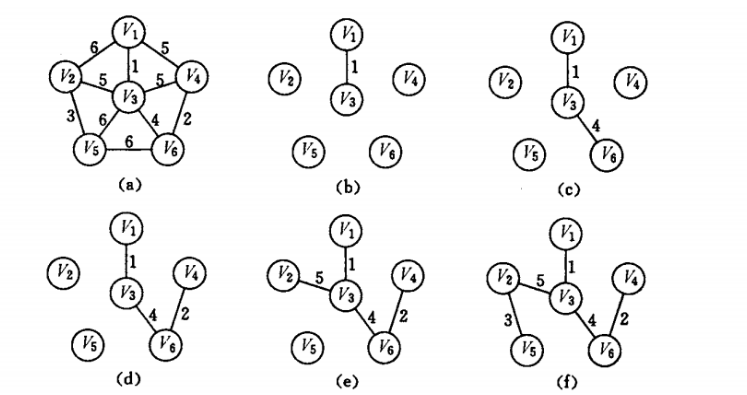
示例：

(a):随机把v1作为初始节点{v1}

(b):在图中选择一个与{v1}连接最小的点v3

(c):选择一个与{v1,v3}连接最小的点v6

(d):选择一个与{v1,v3,v6}连接最小的点v4

(e):选择一个与{v1,v3,v6,v4}连接最小的点v2

(f):选择一个与{v1,v3,v6,v4,v2}连接最小的点v5

生成完毕。

 

时间复杂度

原始prim算法时间复杂度是O(V²)，适合稠密图。

 

python代码

def prim(maps): #maps是边的邻接矩阵,没有边的地方用一个最大值表示
    nodenum = len(maps)
    if nodenum == 0:
        return None
    seleted_node = [0]
    cand_node = [1] * nodenum
    cand_node[0] = -1
    res = []
    while len(seleted_node) < nodenum:
        begin, end, minweight = -1, -1, sys.maxsize        
        for i in seleted_node:
            for j in range(nodenum):
                if cand_node[j] == -1:
                    continue
                if minweight > maps[i][j]:
                    begin, end, minweight = i, j, maps[i][j]
        res.append([begin, end, minweight])   
        seleted_node.append(end)
        cand_node[end] = -1
    return res

 

Kruskal算法

算法思想：

kruskal算法也是一种贪心算法，每次贪心的选择还没被选取的边中权值最小且这条边的两个节点不再同一个连通分量中（也就是这条边不能与已选的边构成环）

 

时间复杂度

O(ElogE) 

 

python代码

def kruskal(maps):
    nodenum = len(maps)
    if nodenum == 0:
        return None
    edge_list = []
    for i in range(nodenum):
        for j in range(nodenum):
            if maps[i][j] != sys.maxsize:
                edge_list.append([i, j, maps[i][j]])
    edge_list.sort(key = lambda x: x[2])
    unionFindSet = [i for i in range(nodenum)]
    res = []
    seleted_edgenum = 0
    for edge in edge_list:
        if seleted_edgenum == nodenum - 1:
            break
        x = find(unionFindSet, edge[0])
        y = find(unionFindSet, edge[1])
        if x != y:
            res.append(edge)
            unionFindSet[x] = y
            seleted_edgenum += 1
    return res

def find(unionFindSet, x):
    if unionFindSet[x] != x:
        unionFindSet[x] = find(unionFindSet, unionFindSet[x])
    return unionFindSet[x]