FM
FM模型

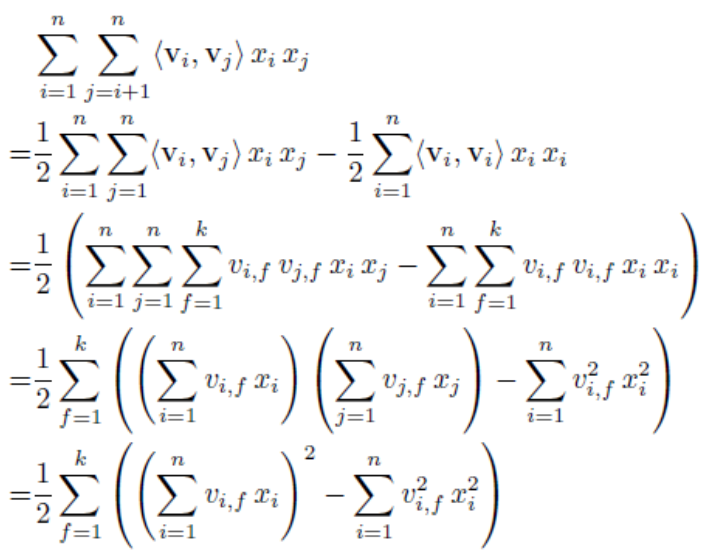
\[\begin{array}{l}
y = {w_0} + \sum\limits_{i = 1}^n {{w_i}{x_i} + \sum\limits_{i = 1}^n {\sum\limits_{j = i + 1}^n { < {V_i},{V_j} > {x_i}{x_j}} } } \\
{\rm{ = }}{w_0} + \sum\limits_{i = 1}^n {{w_i}{x_i} + \frac{1}{2}\sum\limits_{f = 1}^k {\left( {{{\left( {\sum\limits_{i = 1}^n {{v_{if}}{x_i}} } \right)}^2} - \sum\limits_{i = 1}^n {v_{if}^2x_i^2} } \right)} } \\
{\rm{ = }}b + XW + \frac{1}{2}\left( {{{\left( {XV} \right)}^2} - {X^2}{V^2}} \right).sum()
\end{array}\]
时间复杂度分析
FM原始式子的时间复杂度是O(kn2),经过化简后时间复杂度是O(kn)
FM理解
1、 FM算法与线性回归相比增加了特征的交叉。自动选择了所有特征的两两组合,并且给出了两两组合的权重。
2、如果给两两特征的组合都给一个权重的话,需要训练的参数太多了。比如我们有N维的特征,这样的话就需要N*N量级的参数。FM算法的一个优点是减少了需要训练的参数。这个也是参考了矩阵分解的想法。有N个特征,特征间的权重,需要一个N*N的权重矩阵。把这个N*N的矩阵分解成 K*N的矩阵V的乘积,权重矩阵$W = {V^T} * V$ ,此处的K是自己设置的,K<<N。
3、多项式核的SVM和FM的主要区别在于,SVM的二元特征参数是独立的。为什么线性SVM在和多项式SVM在稀疏条件下效果会比较差呢?线性svm只有一维特征,不能挖掘深层次的组合特征在实际预测中并没有很好的表现;而多项式svm正如前面提到的,交叉的多个特征需要在训练集上共现才能被学习到,否则该对应的参数就为0,这样对于测试集上的case而言这样的特征就失去了意义,因此在稀疏条件下,SVM表现并不能让人满意。而FM不一样,通过向量化的交叉,可以学习到不同特征之间的交互,进行提取到更深层次的抽象意义。
FM优点总结
- 引入了特征交叉,相比于线性回归FM的特征在学习时是相互作用的不在是完全独立的。
- 在引入特征交叉的同时限制参数的数目防止参数过多
- 对于每个特征FM都给它学习了一个k维交叉权重${V_i}$,即使两个特征组合没有出现过我们也能间接的学习到这两个特征的组合权重(在推荐系统中我们一般会对特征进行离散化得到高维稀疏特征,这样导致的一个问题就是许多特征两两之间在样本中没有同时出现过,即在训练样本中这两个值没有同时为非0值的情况,导致传统的多项式特征组合方式没法学习到他们的组合权重)
参考博客
https://www.cnblogs.com/AndyJee/p/7879765.html
https://www.jianshu.com/p/a76973b46505






