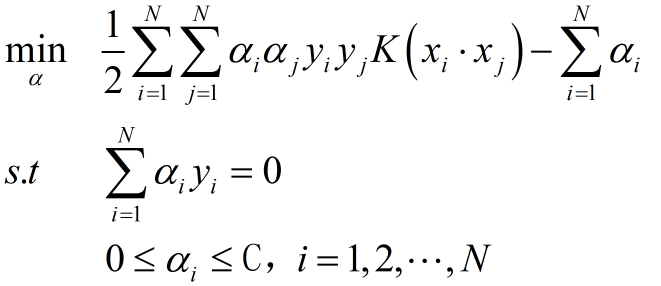SVM

线性可分支持向量机

决策面

\[f\left( x \right) = sign\left( {w \cdot x + b} \right)\]

算法原理

决策面不仅要正确划分数据集并且样本点到决策面的最小几何间隔要最大化

支持向量

训练数据集的样本中与决策面（超平面）距离最近的样本点的实例称为支持向量，支持向量机模型是由这些少量的支持向量确定的。

模型推导

上面的算法原理可以用下面这个数学模型表示：

\[\begin{array}{l}
\mathop {\max }\limits_{w,b} {\rm{  }}\gamma \\
s.t{\rm{      }}{y_i}\left( {\frac{w}{{\left\| w \right\|}} \cdot {x_i} + \frac{b}{{\left\| w \right\|}}} \right) \ge \gamma ,i = 1,2, \cdots ,N
\end{array}\]

等价于：

\[\begin{array}{l}
\mathop {\max }\limits_{w,b} {\rm{  }}\frac{\gamma }{{\left\| w \right\|}}\\
s.t{\rm{      }}{y_i}\left( {w \cdot {x_i} + b} \right) \ge \gamma ,i = 1,2, \cdots ,N
\end{array}\]

令$\gamma  = 1$得到线性可分支持向量机的原始最优化问题：

\[\begin{array}{l}
\mathop {\min }\limits_{w,b} {\rm{  }}\frac{1}{2}{\left\| w \right\|^2}\\
s.t{\rm{      }}{y_i}\left( {w \cdot x{}_i + b} \right) - 1 \ge 0,{\rm{ }}i = 1,2, \cdots ,N
\end{array}\]

对偶算法

引入对偶算法的原因：

1. 对偶问题往往更容易求解
2. 自然的引入核函数，进而推广到非线性分类问题

对偶模型：

\[\begin{array}{l}
\mathop {\min }\limits_\alpha  \frac{1}{2}\sum\limits_{i = 1}^N {\sum\limits_{j = 1}^N {{\alpha _i}{\alpha _j}{y_i}{y_j}\left( {{x_i} \cdot {x_j}} \right) - \sum\limits_{i = 1}^N {{\alpha _i}} } } \\
s.t\sum\limits_{i = 1}^N {{\alpha _i}{y_i} = 0} \\
{\alpha _i} \ge 0,i = 1,2, \cdots ,N
\end{array}\]

\[\begin{array}{l}
w = \sum\limits_{i = 1}^N {{\alpha _i}{y_i}{x_i}} \\
b = {y_j} - \sum\limits_{i = 1}^N {{\alpha _i}{y_i}\left( {{x_i} \cdot {x_j}} \right),} {a_j} > 0
\end{array}\]

线性支持向量机

上面的线性支持向量机只能解决线性可分问题，当存在少量数据不能线性可分时（去掉这些少量的数据剩下的数据能线性可分），意味着这些点不能满足函数间隔大于等于1的约束条件。为了解决这个问题，可以对每个样本点引入一个松弛变量${\xi _i} \ge 0$，这样约束条件就变为：

\[{y_i}\left( {w \cdot {x_i} + b} \right) \ge 1 - {\xi _i}\]

优化模型

\[\begin{array}{l}
\mathop {\min }\limits_{w,b,\xi } \frac{1}{2}{\left\| w \right\|^2} + C\sum\limits_{i = 1}^N {{\xi _i}} \\
s.t{y_i}\left( {w \cdot {x_i} + b} \right) \ge 1 - {\xi _i},i = 1,2, \cdots ,N\\
{\xi _i} \ge 0
\end{array}\]

这个优化问题中$w$的解是唯一的，但$b$的解是不唯一的。

对偶问题

\[\begin{array}{l}
\mathop {\min }\limits_\alpha  \frac{1}{2}\sum\limits_{i = 1}^N {\sum\limits_{j = 1}^N {{\alpha _i}{\alpha _j}{y_i}{y_j}\left( {{x_i} \cdot {x_j}} \right) - \sum\limits_{i = 1}^N {{\alpha _i}} } } \\
s.t\sum\limits_{i = 1}^N {{\alpha _i}{y_i} = 0} \\
{\rm{ 0}} \le {\alpha _i} \le C,i = 1,2, \cdots ,N
\end{array}\]

等价于如下优化问题

\[\mathop {\min }\limits_{w,b} {\rm{ }}\sum\limits_{i = 1}^N {{{\left[ {1 - {y_i}\left( {w \cdot {x_i} + b} \right)} \right]}_ + } + \lambda {{\left\| w \right\|}^2}} \]

 

非线性支持向量机

核函数

$K\left( {x,z} \right) = \phi \left( x \right) \cdot \phi \left( z \right),\phi $是输入空间到特征空间的映射（一般是高维空间）

 

常用核函数

1. 多项式核函数：\[K\left( {x,z} \right) = {\left( {x \cdot z + 1} \right)^p}\]
2. 高斯核函数：\[K\left( {x,z} \right) = \exp \left( { - \frac{{{{\left\| {x - z} \right\|}^2}}}{{2{\sigma ^2}}}} \right)\]

 

非线性支持向量机