写在最前面的
手贱翻开了《珠玑》的最后几章，所以这一篇更多是关于13、14、15章的内容。这篇文章的主要内容是“AVL树”，即平衡树，比红黑树低一个等次。捣乱真惹不起红黑树，情况很复杂；而AVL思路比较清晰。《编程珠玑，字字珠玑》910读书笔记——代码优化更新了，做了点关于“哨兵”的笔记。在这篇文章的末尾，笔者还加了对引用调用的“大彻大悟”。
4篇读书笔记：全在这里
AVL树
学习数据结构的时候，有过一次实验课， 题意大概：英文单词出现次数统计。当时选了哈希表，映射（map），AVL树（平衡树）三种方法来做，是冲着“完成实验老师请吃饭”
去做的。哈希表键值用“除留余数法”，处理冲突用了最简单的开哈希表的“链地址法”。 映射（map）没有深入，只是简单的应用。 比较痛心的是AVL树。
AVL树的旋转
树的旋转分四种：左单旋，右单旋，左右旋转，右左旋转。规定，右子树的高度减去左子树的高度得到此节点的平衡数（也叫平衡因子，balance factor，bf），用bf(node)表示node节点的平衡数。小剖一下这四种情况：
当bf(node)==2的时候，即右子树高度比左子树高，需要将树在node节点左单旋。在作旋转之后，左子树bf+1，右子树bf-1，node节点平衡数归零。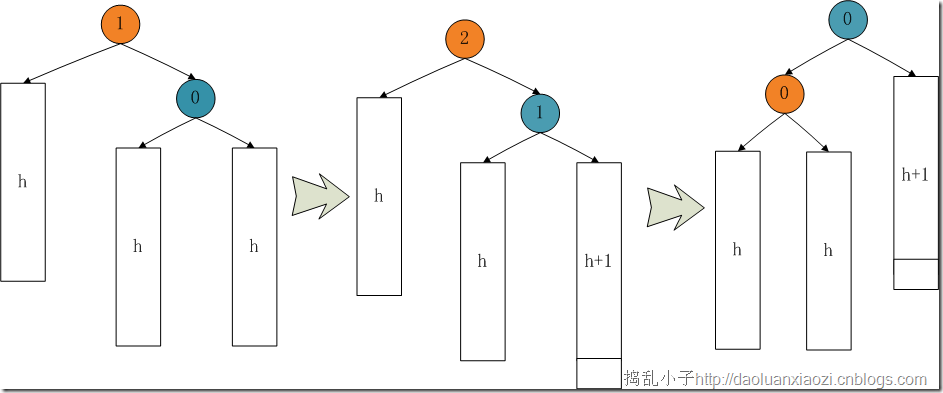 
节点的调整过程很清晰。
再来当bf(node)==-2时候，即右子树比左子树低。需要将树在node节点右单旋。在作选择之后，左子树bf-1，右子树+1，node节点平衡树归零。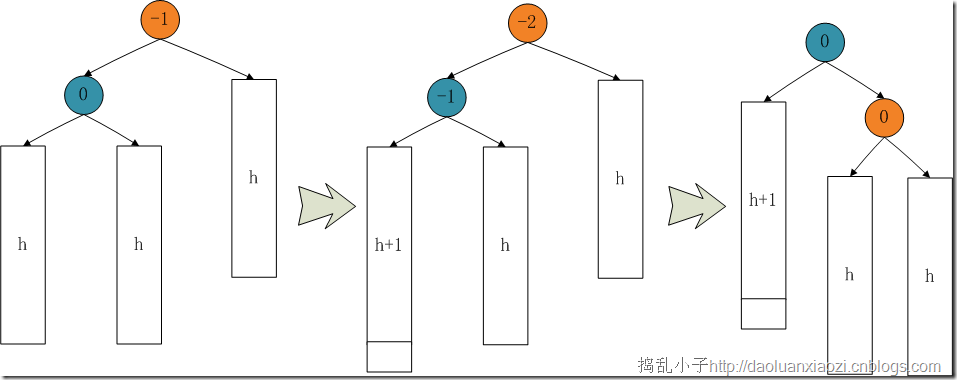 
细心的发现，左单旋和右单旋是一样的，只是反过来罢了。
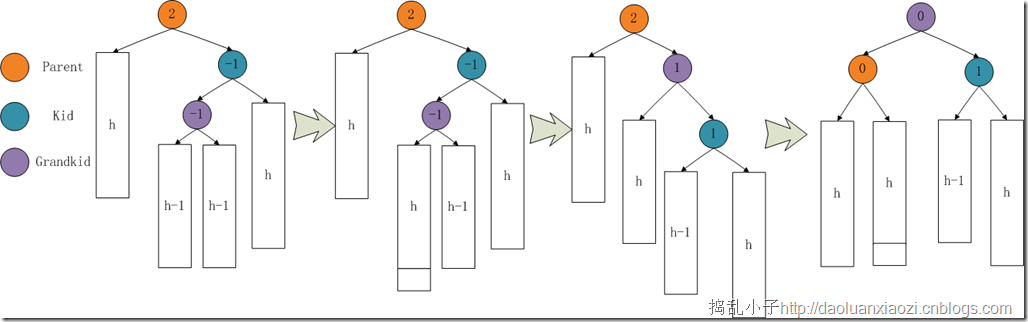
下面的情况复杂了点，但是他们是从上面两种情况延伸过来的，但是这种变化导致它们平衡化的方法也有小小不同。 下面两种情况从子树的内侧插入，导致子树（bf(kid)）和其父亲（bf(parent)）的bf正负相反，先来左右旋转，看图：
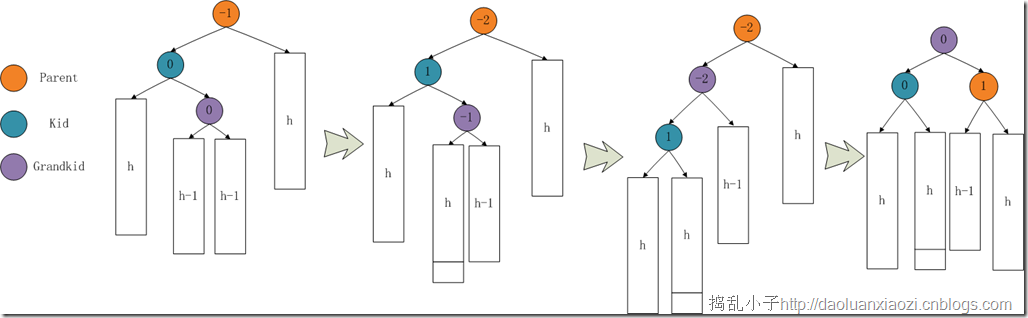
解决之道：kid节点作简单的左单旋，然后parent作简单的右单旋。在过程中需要非常注意节点bf的调整，要分情况进行讨论（把这个槛跨过去，离成功就不远了）。
- 如果从左kid的右子树（grandkid）的左侧插入，
对bf(kid)调整：那么bf(grandkid)<0，在kid作了左单旋之后，grandkid的左侧树被调整为kid的右子树，结果bf(kid)=0；
对bf(parent)调整：在对parent作了右单旋之后，grandkid右子树被调整为parent的左子树，因此如果bf(grandkid)<0，那么bf(parent)=1； - 如果从左kid的右子树（grandkid）的右侧插入，
对bf(kid)调整：那么bf(grandkid)>0，在kid作了左单旋之后，grandkid的左侧树被调整为kid的右子树，结果bf(kid)=-1；
对bf(parent)调整：在对parent作了右单旋之后，grandkid右子树被调整为parent的左子树，因此如果bf(grandkid)<0，那么bf(parent)=0； - 对bf(grandkid)调整：最后，grandkid被调整为新树的根节点，bf(grandkid)=0。
（作一个填空题吧） 结合下面的图来做，属于右左旋转：
对bf(grandkid)调整：最后，grandkid被调整为新树的根节点，bf(grandkid)= 。
答案：<，1，<，0；>，0，>，-1。
可以看出三个节点在调整过程中需要更改bf。最后一种旋转就是右左旋转。不需要太多的分析，跟上面的是一样的，做一个简单的反转。捣乱上图：
构造一个平衡树，即不断将一个新的节点在原树中找到合适的位置，然后调整。那么在“找”的过程中，所经历的节点bf都改变了（+1或者-1）。插入一个节点的做法是： 用栈存储所走过的节点，在找到插入位置后，从插入位置的父节点开始调整，如果此父节点是平衡的，那么从栈中取出父节点，继续调整。
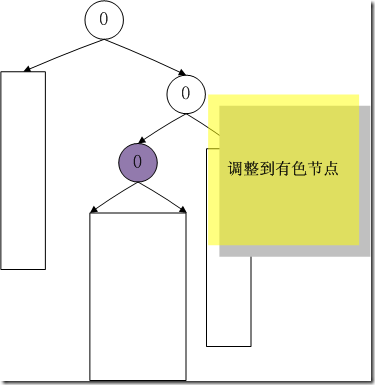
从上面的分析中，只要旋转后，结果旋转的节点都会得到bf(node)=0结果，所以只要旋转后，我们的目的就达到了——树平衡了！所以bf(node)==0d的节点会越来越多，而且是堆积在树的顶层。
因此，不需要每次都调整到树的根节点root，只要调整的节点bf=0，就可以结束了，上面的节点或者兄弟节点已经bf=0。这我在刚接触AVL的时候也很迷惑的地方。
最后我把insert节点的代码给出：
另外，旋转的代码我放在附件里面（如果都贴出来显得很臃肿），再者，附件里有一个“单词统计”的实验报告，有兴趣的同学可以下载看看。当时做实验的时候，AVL统计单词还是挺给力的：
漫谈引用调用
注意：ANSI C里不支持引用调用，而C++提供了引用调用的实现。
正如《effective c++》条款1提及的，指针和引用有应用上的区别。指针所指的对象可以随意更改，而且它的指向可以为null，非常灵活；但引用必须代表一个对象，不能为null，而且它被赋予某个对象后，它将始终代表那个对象知道被销毁为止。例如：
a成为了b的引用，a将不能再引用其他数据。另外，引用变量是否占有内存听说唯有定义（http://topic.csdn.net/u/20100622/15/728477fe-92ab-4e83-8572-0923d37186f1.html），笔者认为可行的方法是程序只在在变量的符号表中添加a，而并没有为a分配任何的内存。
在函数传参的过程中，有值传递，指针传递（都属于c）和引用传递方式（c++）。指针所能做到的，引用也可以做得到。但引用更安全（不至于让它为null），操作起来更方便，同时拥有和指针优点——“节能减排”。来看看：
在function返回后，a依旧为原来的NULL，并没有改变。因为你想，function函数栈内，只保存了指针a的原值NULL，即使a = new TYPE能为a赋予新址，但此a非彼a，在function退栈后，此a将被销毁，而彼a仍旧为NULL。因此如果想更改a指针的内容，必须使用指针的指针或者指针的引用，指针的引用会比较方便。
这时，指针a的值才有所改变。AVL树的程序里有较多的引用调用，读者要注意。捣乱纳闷，这笔记，这大彻大悟，应早在大一就应该写下，羞愧于心，贻笑大方呐。
关于珠玑的总结
珠玑我到底还是把它当作休闲读物了，对于算法或者数据结构的初学者，这一本是力荐的。
附件：
本文完 Thursday, April 26, 2012
