红黑树是一种二叉查找树,它能保证在最坏的情况下,基本的动态操作的时间为O(lgn)。
1. 红黑树的性质
红黑树是一种二叉查找树,与普通二叉查找树不同之处在于以下几个方面:
a) 红黑树在每一个结点上增加一个域来存储该结点的颜色,颜色可以是红(RED)的或者是黑(BLACK)的。因此树的结点包括5个域:color,key,left,right,和p,而二叉查找树是不包括color域的。(有关二叉查找树结点的定义,请参考之前我写的文章http://blog.csdn.net/arge129/article/details/7559845)。
b) 为了便于处理代码中的边界条件,我们采用一个哨兵来代替二叉查找树中的空指针(或引用)null,这个哨兵nil[T]是一个与树内普通结点有相同域的对象,它的color域是BLACK,而其他的四个域可以被设置为任意值。于是在二叉查找树中,我们本来指向null的地方指向了哨兵对象nil[T],并且,我们nil[T]为外结点,而带关键字的结点为内结点。为了编程方便,我们使用一个对象来代替所有的哨兵。
c) 一棵二叉查找树如果满足下面的红黑性质,则为一棵红黑树:
1) 每个结点是或是红的,或是黑的。
2) 根结点是黑的。
3) 每个叶结点(nil[T])是黑的。
4) 如果一个结点是红的,那么它的两个儿子是黑的。
5) 对每个结点,从该结点到其子孙结点的所有路径上包含相同数目的黑结点。
这5条看起来相当的难记,曾在博客上看过一位大哥总结的不错,在这里写一下,向这位牛人致敬。首先,对于第一条来说,这个似乎没什么地方可以违反(当然后面讲到删除的时候会讲),所以直接忽略就行了。对于第二条和第三条,可以总结为黑头黒脚;第四条,那就是“坑爹”。。。第五条,我自己总结的,“一个都不能少”,这是黄宏的一个电影,讲的是他有25个孩子,然后不管怎么数,一个都不能少(挺感人的,可以去看下),所以,对应到性质里,那就是黑结点不管从哪条路径上来数,都是相同的。因此上面的5条,我们就合并为3条:
1) 黑头黒脚。
2)坑爹。
3)一个都不能少。
是不是好记多了呢?其实,红黑树的性质可以看作是红黑树的定义,如果不满足该性质(定义),那就不是红黑树了。那么来看一棵实际的红黑树吧,读者可以从下图中来验证以上的5个性质或者说咱们总结的那3条。
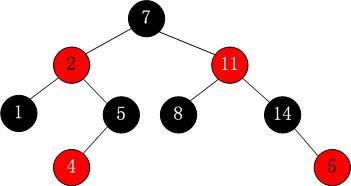
那么红黑树的这些性质,又能使红黑树具有哪些神奇的功能呢,请看下面。
2. 关于红黑树性质的研究
1) 首先,来看下黑高度的定义。红黑树中某一个结点x的黑高度定义为,从x结点出发(不包括该结点)到达一个叶结点的任意一条路径上,黑色结点的个数称为x结点的黑高度。由“一个都不能少”的性质,我们可以知道,黑高度的定义是明确的,因为从该结点出发的所有下降路径都有相同的黑结点个数。红黑树的黑高度定义为其根结点的黑高度。
2) 一棵有n个内结点的红黑树的高度至多为2lg(n+1)。根据“坑爹”这个性质,从根(不包括根结点)到叶结点的任一条简单路径上至少有一半结点是黑色的。两种极端情况为,一种是树中全是黑结点,一种是红黑结点交替出现。假如红结点在某条路径上的个数超过一半,则必然出现两个连续的红结点的情况,而这与”坑爹“性质矛盾,因此不可能出现红结点在某条路径上超过一半的情况。因此红黑树也确保了没有一条路径会比其他路径长出两倍,因而是接近平衡的。具体的证明参考下算法导论吧,这里写一些证明也没多大意义。根据这个性质,我们可以说,基于红黑树的一些操作可以在O(lgn)时间内完成。
3.代码实现(Java)
本篇主要讨论了红黑树的基本性质,因此在此仅给出Java版本的结点定义,关于红黑树的其他操作,后序博客来完成。谢谢关注。(*^__^*)
1 /**
2 * 结点颜色
3 * @author Alfred
4 */
5 public enum NodeColor {
6 RED, BLACK
7 }
1 /**
2 * 红黑树结点定义
3 * @author Alfred
4 */
5 public class RBTreeNode {
6 private int key;
7 private NodeColor color;
8 private RBTreeNode parent;
9 private RBTreeNode left;
10 private RBTreeNode right;
11 public RBTreeNode(int key, NodeColor nodeColor){
12 this.key = key;
13 this.color = nodeColor;
14 }
15 public String toString(){
16 return ""+key+":"+color+" ";
17 }
18 /**
19 * @return the key
20 */
21 public int getKey() {
22 return key;
23 }
24 /**
25 * @param key the key to set
26 */
27 public void setKey(int key) {
28 this.key = key;
29 }
30 /**
31 * @return the color
32 */
33 public NodeColor getColor() {
34 return color;
35 }
36 /**
37 * @param color the color to set
38 */
39 public void setColor(NodeColor color) {
40 this.color = color;
41 }
42 /**
43 * @return the parent
44 */
45 public RBTreeNode getParent() {
46 return parent;
47 }
48 /**
49 * @param parent the parent to set
50 */
51 public void setParent(RBTreeNode parent) {
52 this.parent = parent;
53 }
54 /**
55 * @return the left
56 */
57 public RBTreeNode getLeft() {
58 return left;
59 }
60 /**
61 * @param left the left to set
62 */
63 public void setLeft(RBTreeNode left) {
64 this.left = left;
65 }
66 /**
67 * @return the right
68 */
69 public RBTreeNode getRight() {
70 return right;
71 }
72 /**
73 * @param right the right to set
74 */
75 public void setRight(RBTreeNode right) {
76 this.right = right;
77 }
78 }



 浙公网安备 33010602011771号
浙公网安备 33010602011771号