【LeetCode刷题】1353. 最多可以参加的会议数目
给你一个数组 events,其中 events[i] = [startDayi, endDayi] ,表示会议 i 开始于 startDayi ,结束于 endDayi 。
你可以在满足 startDayi <= d <= endDayi 中的任意一天 d 参加会议 i 。注意,一天只能参加一个会议。
请你返回你可以参加的 最大 会议数目。
示例 1:
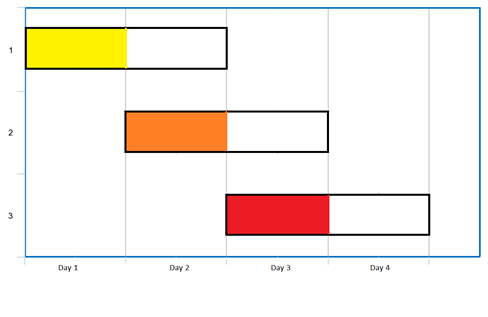
输入:events = [[1,2],[2,3],[3,4]]
输出:3
解释:你可以参加所有的三个会议。
安排会议的一种方案如上图。
第 1 天参加第一个会议。
第 2 天参加第二个会议。
第 3 天参加第三个会议。
示例 2:
输入:events= [[1,2],[2,3],[3,4],[1,2]]
输出:4
示例 3:
输入:events = [[1,4],[4,4],[2,2],[3,4],[1,1]]
输出:4
示例 4:
输入:events = [[1,100000]]
输出:1
示例 5:
输入:events = [[1,1],[1,2],[1,3],[1,4],[1,5],[1,6],[1,7]]
输出:7
提示:
- 1 <= events.length <= 10^5
- events[i].length == 2
- 1 <= events[i][0] <= events[i][1] <= 10^5
贪心思路
发现这么写,比较简单。。。就按照结束时间升序排序即可,然后用个set,对区间从前往后遍历,如果这个点上没安排会议就添加进去。。对于 100000*[1,100000]100000∗[1,100000]这种例子不太可行,数据水(本人菜鸡大佬们轻喷
我在这补充下我这个为什么要根据结束时间升序排序。。有的小伙伴有点模糊,假设已经安排了一些会议,我们现在再安排的会议肯定是不能和之前冲突的对吧。有这么几种选择
再安排剩下的里面,具有最早开始时间的
再安排剩下的里面,持续时间最短的
再安排剩下的里面,具有最早结束时间的。
选择第一种,极端情况是开始很早,持续时间很长,选择第二种,持续时间很短,开始很晚,选择第三种最早结束时间,可以理解为最早开始时间+持续时间也最短,所以按照最早结束时间升序排序就是这么来的。
代码
class Solution {
public:
int maxEvents(vector<vector<int>>& events) {
sort(events.begin(), events.end(), [](const vector<int>& e1, const vector<int>& e2) {
return e1[1] < e2[1];
});
unordered_set<int> res;
for(vector<int> e: events) {
for(int d = e[0]; d <= e[1]; d++) {
if(res.find(d) == res.end()) {
res.insert(d);
break;
}
}
}
return res.size();
}
};
贪心+优先队列方法
这是一道典型的扫描算法题。由于每个时间点最多参加一个会议,我们可以从1开始遍历所有时间。
对于每一个时间点,所有在当前时间及之前时间开始,并且在当前时间还未结束的会议都是可参加的。显然,在所有可参加的会议中,选择结束时间最早的会议是最优的,因为其他会议还有更多的机会可以去参加。
怎样动态获得当前结束时间最早的会议呢?我们可以使用一个小根堆记录所有当前可参加会议的结束时间。在每一个时间点,我们首先将当前时间点开始的会议加入小根堆,再把当前已经结束的会议移除出小根堆(因为已经无法参加了),然后从剩下的会议中选择一个结束时间最早的去参加。
为了快速获得当前时间点开始的会议,我们以O(N)O(N)时间预处理得到每个时间点开始的会议的序号。
算法总的时间复杂度为O(T\log N)O(TlogN)(这里的TT为时间范围)。
参考代码
const int MAX = 1e5 + 1;
class Solution {
public:
int maxEvents(vector<vector<int>>& events) {
vector<vector<int>> left(MAX);
for (int i = 0; i < events.size(); ++i)
left[events[i][0]].emplace_back(i);
int ans = 0;
priority_queue<int, vector<int>, greater<>> pq;
for (int i = 1; i < MAX; ++i) {
for (int j : left[i])
pq.push(events[j][1]);
while (!pq.empty() && pq.top() < i)
pq.pop();
if (!pq.empty()) {
pq.pop();
ans++;
}
}
return ans;
}
};



