5. Logistic回归
一、介绍
Logistic回归是广泛应用的机器学习算法,虽然名字里带“回归”,但是它实际上是一种分类方法,主要用于两分类问题(即输出只有两种,分别代表两个类别)。
面对一个回归或者分类问题,建立代价函数(损失函数),使用最优化算法(梯度上升法、改进的随机梯度上升法),找到最佳拟合参数,将数据拟合到一个logit函数(或者叫做logistic函数)中,得到定性变量y,比如y=0或1,从而预测事件发生的概率。
二、线性回归
从线性回归说,多维空间中存在的样本点,用特征的线性组合去拟合空间中点的分布和轨迹。如下图所示:
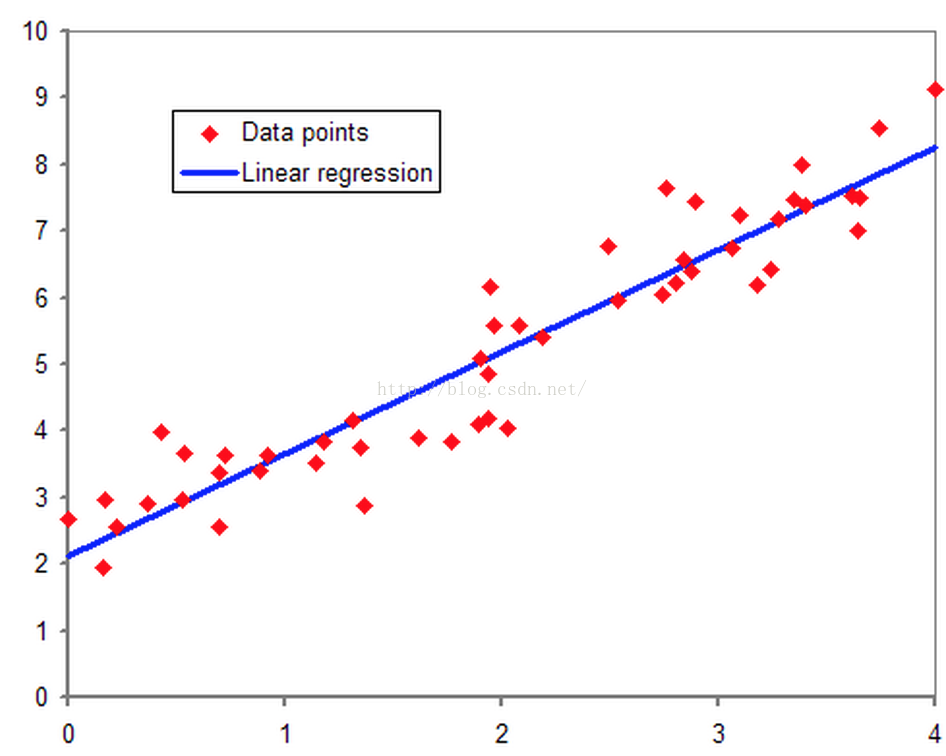
线性回归能对连续值结果进行预测,现实生活中存在另一种分类-----是与否的二分类问题。比如医生需要判断病人是否生病,银行要判断一个人的信用程度是否达到可以给他发信用卡的程度,邮件收件箱要自动对邮件分类为正常邮件和垃圾邮件等等。
当然,既然能够用线性回归预测出连续值结果,那根据结果设定一个阈值是不是就可以解决这个问题了呢?事实是,对于很标准的情况,确实可以。下图中X为数据点肿瘤的大小,Y为观测结果是否是恶性肿瘤。如hθ(x)所示,构建线性回归模型,然后设定一个阈值0.5,预测hθ(x)≥0.5的这些点为恶性肿瘤,而hθ(x)<0.5为良性肿瘤。
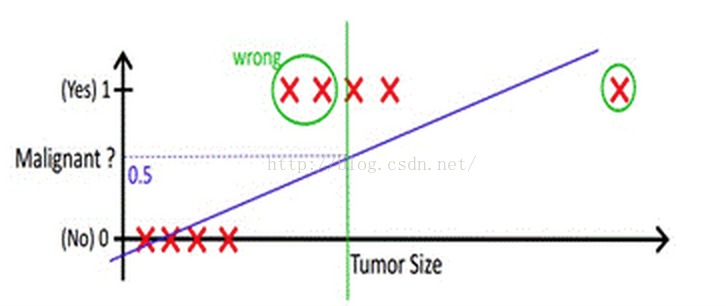
上图中突然有一个wrong的数据点,再根据设定的0.5,得出的分类就是错误的(良性肿瘤错误认为是恶性肿瘤),而现实生活中分类问题的数据,会比上述举例更复杂,借助线性回归+阈值的方式,很难完成一个鲁棒性很好的分类器。
相比线性回归,逻辑回归:
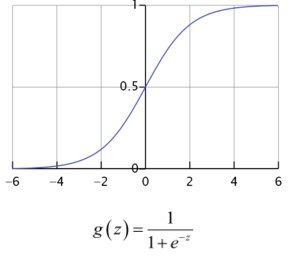
1. 线性回归的结果是一个连续值,值的范围是无法限定的,假设回归的结果都是无法限定的值,那做出一个判定就很难了。能将结果做一个映射,输出(0,1) 的一个概率值,这个问题就很清楚了。有这样一个简单的函数,可以做到这样的映射---sigmoid函数。
说明:从sigmoid函数图像可以看出,函数 hθ(x) = g(z): 在z=0的时候.函数值1/2,随着 z 逐渐变小函数值趋于0,z 逐渐变大函数值逐渐趋于1,而这正是一个概率的范围。
我们定义线性回归的预测函数为hθ(x) = θTX,那么逻辑回归的输出hθ(x) = g( θTX ),其中 g( z ) 函数就是上述sigmoid函数.
hθ(x) = g( θTX ) ≥ 0.5, 则 θTX ≥ 0, 意味着类别为 1;
hθ(x) = g( θTX ) < 0.5, 则 θTX < 0, 意味着类别为 0;
所以可以认为 θTX =0 是一个决策边界,当它 >0 或 <0 时,逻辑回归模型预测出不同的分类结果。
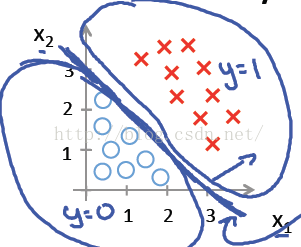
2. 逻辑回归可以做出直线、圆或者是曲线这样的判定边界,比较好地将两类样本分开。
说明:假设 hθ(x)=g(θ0+θ1X1+θ2X2),其中θ0 ,θ1 ,θ2分别取-3, 1, 1。则当−3+X1+X2 ≥ 0时, y = 1即类别为1; 则X1+X2 = 3是一个判定边界,图形表示如下,刚好把图上的两类点区分开来:
假设hθ(x) 比较复杂,hθ(x) = g(θ0+θ1X1+θ2X2+ θ3 X12+ θ4X22) ,其中θ0 ,θ1 ,θ2,θ3 ,θ4 分别取-1, 0, 0,1,1,则当 -1 + x12+x22 ≥ 0 时,y = 1即类别为1; 则x12+x22 = 1是一个判定边界,图形表示如下:
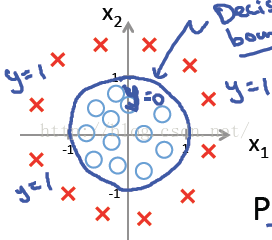
所以,只要我们的hθ(x)设计足够合理,准确的说是g(θTx)中θTx足够复杂,能在不同的情形下,拟合出不限于线性的判定边界。
三、求解θ
假设我们有n个独立的训练样本{(x1, y1) ,(x2, y2),…, (xn, yn)},类别y = {0, 1}。那每一个观察到的样本(xi, yi)出现的概率是:
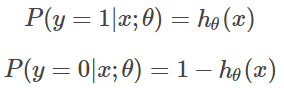
y的取值为0 或 1,所以,上式等价于:
那整个样本集,n个独立的样本出现的似然函数为(因为每个样本都是独立的,所以n个样本出现的概率就是它们各自出现的概率相乘):
连乘不好处理,取自然对数,转成相加:
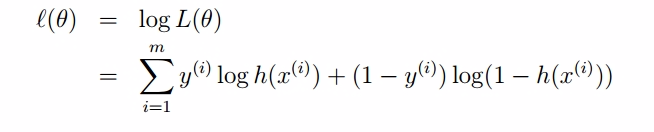
经过化简得到:
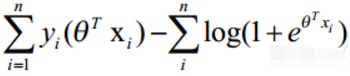
该似然函数在这里表示的是:参数取值为θ时,取得当前这个样本集的可能性。使参数为θ的似然函数L(θ)极大化,然后极大值对应的θ就是我们的估计。
假如需要求如下函数的最大值:
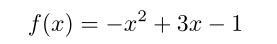
函数的导数为:
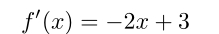
所以 x=1.5即取得函数的最大值1.25。
同样的,我们对刚刚的对数似然函数logL(θ)即l(θ)求导:
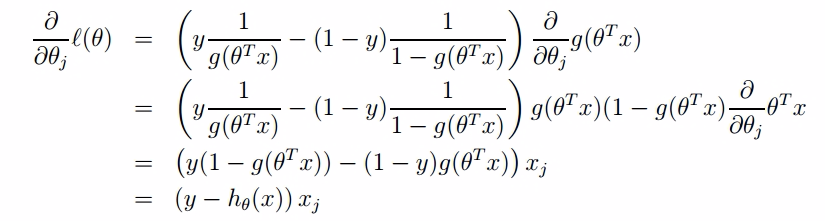
终于可以说梯度上升了……利用迭代公式:
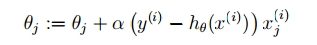
参数α叫学习率,就是每一步走多远,这个参数蛮关键的。如果设置的太多,那么很容易就在最优值附近徘徊,因为步伐太大了。它带来的好处是能很快的从远离最优值的地方回到最优值附近,只是在最优值附近的时候,它有心无力了。但如果设置的太小,那收敛速度就太慢了,向蜗牛一样,虽然会落在最优的点,但是速度太慢。所以学习率可以改进,开始迭代时,学习率大,慢慢的接近最优值的时候,学习率变小就可以了,即随机梯度下降算法。
所以,最终我们计算过程(训练过程)如下:
1. 根据权重和训练样本计算估计值
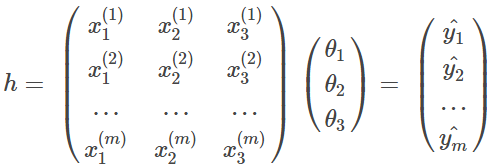
2.计算误差
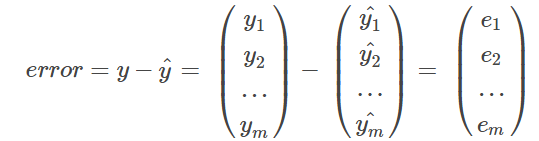
3. 迭代更新
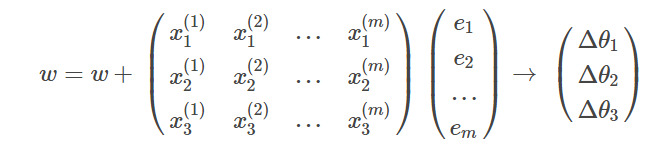
迭代停止条件:到达限定迭代次数 或者 误差 <= 设定误差的最小值。
说明:以上过程中,n 和 m等价,w 和 θ等价。
四、 代码
1 import numpy as np 2 import re 3 from pandas import DataFrame 4 import time as time 5 import matplotlib.pyplot as plt 6 import math 7 8 def get_data(filename): #读取数据 9 f = open(filename) 10 data = DataFrame(columns=['x0','x1','x2','label']) #构造DataFrame存放数据,列名为x与y 11 line = f.readline() 12 line = line.strip() 13 p = re.compile(r'\s+') #由于数据由若干个空格分隔,构造正则表达式分隔 14 while line: 15 line = line.strip() 16 linedata = p.split(line) 17 data.set_value(len(data),['x0','x1','x2','label'],[1,float(linedata[0]),float(linedata[1]),int(linedata[2])]) #数据存入DataFrame 18 line = f.readline() 19 return np.array(data.loc[:,['x0','x1','x2']]),np.array(data['label']) 20 def sigmoid(x): 21 return 1.0/(1+np.exp(-x)) 22 def stocGradAscent(dataMat,labelMat,alpha = 0.01): #随机梯度上升 23 start_time = time.time() #记录程序开始时间 24 m,n = dataMat.shape 25 weights = np.ones((n,1)) #分配权值为1 26 for i in range(m): 27 h = sigmoid(np.dot(dataMat[i],weights).astype('int64')) #注意:这里两个二维数组做内积后得到的dtype是object,需要转换成int64 28 error = labelMat[i]-h #误差 29 weights = weights + alpha*dataMat[i].reshape((3,1))*error #更新权重 30 duration = time.time()-start_time 31 print('time:',duration) 32 return weights 33 def gradAscent(dataMat,labelMat,alpha = 0.01,maxstep = 1000): #批量梯度上升 34 start_time = time.time() 35 m,n = dataMat.shape 36 weights = np.ones((n,1)) 37 for i in range(maxstep): 38 h = sigmoid(np.dot(dataMat,weights).astype('int64')) #这里直接进行矩阵运算 39 labelMat = labelMat.reshape((100,1)) #label本为一维,转成2维 40 error = labelMat-h #批量计算误差 41 weights = weights + alpha*np.dot(dataMat.T,error) #更新权重 42 duration = time.time()-start_time 43 print('time:',duration) 44 return weights 45 def betterStoGradAscent(dataMat,labelMat,alpha = 0.01,maxstep = 150): 46 start_time = time.time() 47 m,n = dataMat.shape 48 weights = np.ones((n,1)) 49 for j in range(maxstep): 50 for i in range(m): 51 alpha = 4/(1+i+j) + 0.01 #设置更新率随迭代而减小 52 h = sigmoid(np.dot(dataMat[i],weights).astype('int64')) 53 error = labelMat[i]-h 54 weights = weights + alpha*dataMat[i].reshape((3,1))*error 55 duration = time.time()-start_time 56 print('time:',duration) 57 return weights 58 def show(dataMat, labelMat, weights): 59 #dataMat = np.mat(dataMat) 60 #labelMat = np.mat(labelMat) 61 m,n = dataMat.shape 62 min_x = min(dataMat[:, 1]) 63 max_x = max(dataMat[:, 1]) 64 xcoord1 = []; ycoord1 = [] 65 xcoord2 = []; ycoord2 = [] 66 for i in range(m): 67 if int(labelMat[i]) == 0: 68 xcoord1.append(dataMat[i, 1]); ycoord1.append(dataMat[i, 2]) 69 elif int(labelMat[i]) == 1: 70 xcoord2.append(dataMat[i, 1]); ycoord2.append(dataMat[i, 2]) 71 fig = plt.figure() 72 ax = fig.add_subplot(111) 73 ax.scatter(xcoord1, ycoord1, s=30, c="red", marker="s") 74 ax.scatter(xcoord2, ycoord2, s=30, c="green") 75 x = np.arange(min_x, max_x, 0.1) 76 y = (-float(weights[0]) - float(weights[1])*x) / float(weights[2]) 77 ax.plot(x, y) 78 plt.xlabel("x1"); plt.ylabel("x2") 79 plt.show() 80 81 if __name__=='__main__': 82 dataMat,labelMat = get_data('data1.txt') 83 weights = gradAscent(dataMat,labelMat) 84 show(dataMat,labelMat,weights)
参考:

