极大似然法估计
极大似然法估计
欢迎关注我的博客:http://www.cnblogs.com/xujianqing/
举个例子:
张无忌和宋青书分别给周芷若送一个糖果,周芷若最后只接受一个糖果,问周芷若接受了谁的糖果。大部分的人肯定会说,当然是张无忌了。
这里面就蕴含了极大似然的思想。因为周芷若接受张无忌的概率大于宋青书呀,而故事的最后周芷若接受了一颗糖果这个事实发生了,所以我们自然选择发生概率大的那个了。
一个函数总体的分布是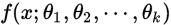 。样本
。样本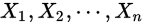 是从总体中抽出的样本,这些样本独立同分布(是极大似然的前提条件),则这些样本
是从总体中抽出的样本,这些样本独立同分布(是极大似然的前提条件),则这些样本 服从的分布就是:
服从的分布就是:
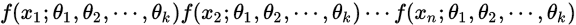
因为独立同分布,所以可以乘。把上面函数记为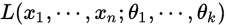
 当我们固定
当我们固定 时,看做是
时,看做是 的函数,
的函数,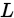 是一个概率密度函数或者概率函数。
是一个概率密度函数或者概率函数。
这样理解:若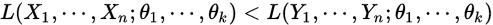 ,则我们可以认为
,则我们可以认为 这个点出现的可能性要大于
这个点出现的可能性要大于 这些点出现的概率。
这些点出现的概率。
 当我们固定
当我们固定 时,
时, 看做是
看做是 的函数,
的函数,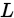 是一个似然估计,这个函数在一个固定的观察结果
是一个似然估计,这个函数在一个固定的观察结果 的取值下,参数值
的取值下,参数值 可以看成是导致这个结果出现的原因,因为出现了周芷若接受糖果的事了,所以我们就让这件事情发生的概率最大,所以就叫张无忌去送糖果。张无忌就是那个
可以看成是导致这个结果出现的原因,因为出现了周芷若接受糖果的事了,所以我们就让这件事情发生的概率最大,所以就叫张无忌去送糖果。张无忌就是那个 。当然这里面的
。当然这里面的 是有一定的值的(并不是任何值都可以),并不是随便一个人送糖果都可以的对吧。这里还包含了贝叶斯学派和频率主义学派两家的观点问题。频率主义学派认为参数是虽然是未知的,但是它是一个客观存在的固定值,因此可以通过优化似然函数等一些准则来确定参数值;但是贝叶斯学派认为参数是未观察到的随机变量,其本身也可以有分布,因此可以假定参数服从一个先验分布,然后基于观测到的数据来计算参数的后验分布。上面的估计方法就是传统的频率主义学派所认为的观点,就是一个事件的概率分布参数是存在的,我们需要优化似然函数这样的函数来求解得到参数。既然能发生,说明它出现的概率就是大,就像能考到清北的孩子优秀的概率肯定大于一般高校的孩子(一般这样认为)。
是有一定的值的(并不是任何值都可以),并不是随便一个人送糖果都可以的对吧。这里还包含了贝叶斯学派和频率主义学派两家的观点问题。频率主义学派认为参数是虽然是未知的,但是它是一个客观存在的固定值,因此可以通过优化似然函数等一些准则来确定参数值;但是贝叶斯学派认为参数是未观察到的随机变量,其本身也可以有分布,因此可以假定参数服从一个先验分布,然后基于观测到的数据来计算参数的后验分布。上面的估计方法就是传统的频率主义学派所认为的观点,就是一个事件的概率分布参数是存在的,我们需要优化似然函数这样的函数来求解得到参数。既然能发生,说明它出现的概率就是大,就像能考到清北的孩子优秀的概率肯定大于一般高校的孩子(一般这样认为)。
所以我们就去求当满足取样值的条件下,似然函数最大的那个参数就ok即:
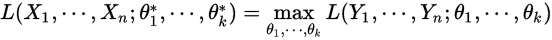
即选择使得似然条件最大的参数作为原始参数的估计值。当然为了使得似然函数计算和不至于上溢,选择对原始似然函数去对数,叫做对数似然,于是就是优化下面的函数
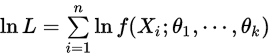
为了使得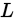 达到最大,只需对
达到最大,只需对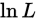 取偏导,就可以建立方程组:
取偏导,就可以建立方程组: